Correlation function
Encyclopedia
A correlation function is the correlation
between random variable
s at two different points in space or time, usually as a function of the spatial or temporal distance between the points. If one considers the correlation function between random variables representing the same quantity measured at two different points then this is often referred to as an autocorrelation function being made up of autocorrelation
s. Correlation functions of different random variables are sometimes called cross correlation functions to emphasise that different variables are being considered and because they are made up of cross correlations.
Correlation functions are a useful indicator of dependencies as a function of distance in time or space, and they can be used to assess the distance required between sample points for the values to be effectively uncorrelated. In addition, they can form the basis of rules for interpolating values at points for which there are observations.
Correlation functions used in astronomy
, financial analysis
, and statistical mechanics
differ only in the particular stochastic processes they are applied to. In quantum field theory
there are correlation functions over quantum distributions
.
where
is described in the article on correlation
. In this definition, it has been assumed that the stochastic variable is scalar-valued. If it is not, then more complicated correlation functions can be defined. For example, if one has a vector Xi(s), then one can define the matrix of correlation functions
or a scalar, which is the trace of this matrix. If the probability distribution
has any target space symmetries, i.e. symmetries in the space of the stochastic variable (also called internal symmetries), then the correlation matrix will have induced symmetries. If there are symmetries of the space (or time) in which the random variables exist (also called spacetime symmetries
) then the correlation matrix will have special properties. Examples of important spacetime symmetries are —
n is
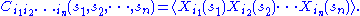
If the random variable has only one component, then the indices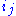
are redundant. If there are symmetries, then the correlation function can be broken up into irreducible representations of the symmetries — both internal and spacetime.
The case of correlations of a single random variable can be thought of as a special case of autocorrelation of a stochastic process on a space which contains a single point.
s and led to the notion of the Ito calculus
.
The Feynman path integral
in Euclidean space generalizes this to other problems of interest to statistical mechanics
. Any probability distribution which obeys a condition on correlation functions called reflection positivity lead to a local quantum field theory
after Wick rotation
to Minkowski spacetime. The operation of renormalization
is a specified set of mappings from the space of probability distributions to itself. A quantum field theory
is called renormalizable if this mapping has a fixed point which gives a quantum field theory.
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
between random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s at two different points in space or time, usually as a function of the spatial or temporal distance between the points. If one considers the correlation function between random variables representing the same quantity measured at two different points then this is often referred to as an autocorrelation function being made up of autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
s. Correlation functions of different random variables are sometimes called cross correlation functions to emphasise that different variables are being considered and because they are made up of cross correlations.
Correlation functions are a useful indicator of dependencies as a function of distance in time or space, and they can be used to assess the distance required between sample points for the values to be effectively uncorrelated. In addition, they can form the basis of rules for interpolating values at points for which there are observations.
Correlation functions used in astronomy
Correlation function (astronomy)
In astronomy, a correlation function describes the distribution of galaxies in the universe. By default, correlation function refers to the two-point autocorrelation function. For a given distance, the two-point autocorrelation function is a function of one variable which describes the...
, financial analysis
Financial analysis
Financial analysis refers to an assessment of the viability, stability and profitability of a business, sub-business or project....
, and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
differ only in the particular stochastic processes they are applied to. In quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
there are correlation functions over quantum distributions
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
.
Definition
For random variables X(s) and X(t) at different points s and t of some space, the correlation function iswhere
is described in the article on correlationCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
. In this definition, it has been assumed that the stochastic variable is scalar-valued. If it is not, then more complicated correlation functions can be defined. For example, if one has a vector Xi(s), then one can define the matrix of correlation functions
or a scalar, which is the trace of this matrix. If the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
has any target space symmetries, i.e. symmetries in the space of the stochastic variable (also called internal symmetries), then the correlation matrix will have induced symmetries. If there are symmetries of the space (or time) in which the random variables exist (also called spacetime symmetries
Spacetime symmetries
Spacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...
) then the correlation matrix will have special properties. Examples of important spacetime symmetries are —
- translational symmetry yields C(s,s
' ) = C(s − s' ) where s and s' are to be interpreted as vectors giving coordinates of the points - rotational symmetry in addition to the above gives C(s, s
' ) = C(|s − s' |) where |x| denotes the norm of the vector x (for actual rotations this is the Euclidean or 2-norm).
n is
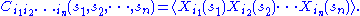
If the random variable has only one component, then the indices
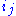are redundant. If there are symmetries, then the correlation function can be broken up into irreducible representations of the symmetries — both internal and spacetime.The case of correlations of a single random variable can be thought of as a special case of autocorrelation of a stochastic process on a space which contains a single point.
Properties of probability distributions
With these definitions, the study of correlation functions is equivalent to the study of probability distributions. Probability distributions defined on a finite number of points can always be normalized, but when these are defined over continuous spaces, then extra care is called for. The study of such distributions started with the study of random walkRandom walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
s and led to the notion of the Ito calculus
Ito calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
.
The Feynman path integral
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
in Euclidean space generalizes this to other problems of interest to statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. Any probability distribution which obeys a condition on correlation functions called reflection positivity lead to a local quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
after Wick rotation
Wick rotation
In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
to Minkowski spacetime. The operation of renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
is a specified set of mappings from the space of probability distributions to itself. A quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
is called renormalizable if this mapping has a fixed point which gives a quantum field theory.
See also
- AutocorrelationAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
- Covariance functionCovariance functionIn probability theory and statistics, covariance is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field...
- Pearson product-moment correlation coefficientPearson product-moment correlation coefficientIn statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
- Correlation function (astronomy)Correlation function (astronomy)In astronomy, a correlation function describes the distribution of galaxies in the universe. By default, correlation function refers to the two-point autocorrelation function. For a given distance, the two-point autocorrelation function is a function of one variable which describes the...
- Correlation function (statistical mechanics)Correlation function (statistical mechanics)In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function, and describes how microscopic variables at different positions are correlated....
- Correlation function (quantum field theory)Correlation function (quantum field theory)In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
- Mutual information
- Radial distribution functionRadial distribution functionIn statistical mechanics, a radial distribution function , g, describes how the atomic density varies as a function of the distance from one particular atom....