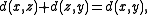In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, convex metric spaces are, intuitively, metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

s with the property any "segment" joining two points in that space has other points in it besides the endpoints.

Formally, consider a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

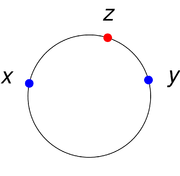
 (X, d) and let x and y be two points in X. A point z in X is said to be between x and y if all three points are distinct, and

that is, the triangle inequality

Triangle inequality

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....

 becomes an equality. A convex metric space is a metric space (X, d) such that, for any two distinct points x and y in X, there exists a third point z in X lying between x and y.

Metric convexity:

• does not imply convexity in the usual sense for subsets of Euclidean space
  Euclidean space
  In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
  
   (see the example of the rational numbers)
• nor does it imply path-connectedness (see the example of the rational numbers)
• nor does it imply geodesic convexity
  Geodesic convexity
  In mathematics — specifically, in Riemannian geometry — geodesic convexity is a natural generalization of convexity for sets and functions to Riemannian manifolds...
  
   for Riemannian manifolds (consider, for example, the Euclidean plane with a closed disc removed).

Examples

• Euclidean spaces, that is, the usual three-dimensional space and its analogues for other dimensions, are convex metric spaces. Given any two distinct points and 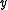in such a space, the set of all points satisfying the above "triangle equality" forms the line segment
  Line segment
  In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
  
   between and which always has other points except and 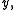in fact, it has a continuum of points.

• Any convex set
  Convex set
  In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
  
   in a Euclidean space is a convex metric space with the induced Euclidean norm. For closed set
  Closed set
  In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
  
  s the converse
  Contraposition
  In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
  
   is also true: if a closed subset of a Euclidean space together with the induced distance is a convex metric space, then it is a convex set (this is a particular case of a more general statement to be discussed below).
• A circle
  Circle
  A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
  
   is a convex metric space, if the distance between two points is defined as the length of the shortest arc on the circle connecting them.

Metric segments

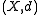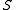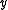Let be a metric space (which is not necessarily convex). A subset of is called a metric segment between two distinct points and in 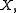if there exists a closed interval 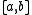on the real line and an isometry

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

such that 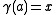and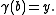

It is clear that any point in such a metric segment 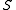except for the "endponts" and 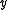is between and 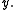As such, if a metric space 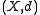admits metric segments between any two distinct points in the space, then it is a convex metric space.

The converse

Contraposition

In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...

 is not true, in general. The rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s form a convex metric space with the usual distance, yet there exists no segment connecting two rational numbers which is made up of rational numbers only. If however, 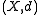is a convex metric space, and, in addition, it is complete, one can prove that for any two points 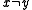in 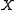there exists a metric segment connecting them (which is not necessarily unique).

Convex metric spaces and convex sets

As mentioned in the examples section, closed subsets of Euclidean spaces are convex metric spaces if and only if they are convex sets. It is then natural to think of convex metric spaces as generalizing the notion of convexity beyond Euclidean spaces, with usual linear segments replaced by metric segments.

It is important to note, however, that metric convexity defined this way does not have one of the most important properties of Euclidean convex sets, that being that the intersection of two convex sets is convex. Indeed, as mentioned in the examples section, a circle, with the distance between two points measured along the shortest arc connecting them, is a (complete) convex metric space. Yet, if and 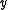are two points on a circle diametrally opposite to each other, there exist two metric segments connecting them (the two arcs into which these points split the circle), and those two arcs are metrically convex, but their intersection is the set 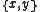which is not metrically convex.