
Essentially unique
Encyclopedia
In mathematics
, the term essentially unique is used to indicate that while some object is not the only one that satisfies certain properties, all such objects are "the same" in some sense appropriate to the circumstances. This notion of "sameness" is often formalized using an equivalence relation
.
A related notion is a universal property
, where an object is not only essentially unique, but unique up to a unique isomorphism
(meaning that it has trivial automorphism group). In general given two isomorphic examples of an essentially unique object, there is no natural (unique) isomorphism between them.
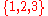 or
or 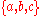 .
.
In this case the non-uniqueness of the isomorphism (does one match 1 to a or to c?) is reflected in the symmetric group
.
On the other hand, there is an essentially unique ordered set of any given finite cardinality: if one writes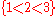 and
and 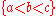 , then the only order-preserving isomorphism maps 1 to a, 2 to b, and 3 to c.
, then the only order-preserving isomorphism maps 1 to a, 2 to b, and 3 to c.
s. We would find that there is an essentially unique group containing exactly 3 elements, the cyclic group
of order three. No matter how we choose to write those three elements and denote the group operation, all such groups are isomorphic, hence, "the same".
On the other hand, there is not an essentially unique group with exactly 4 elements, as there are two non-isomorphic examples: the cyclic group of order 4 and the Klein four group.
, strictly positive
, locally finite measure
on the real line
. The solution to this problem is essentially unique: any such measure must be a constant multiple of Lebesgue measure
. Specifying that the measure of the unit interval should be 1 then determines the solution uniquely.
, simply connected manifold
s. We would find an essentially unique solution to this problem: the 2-sphere. In this case, the solution is unique up to homeomorphism
.
of a semisimple Lie group may not be unique, but is unique up to conjugation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the term essentially unique is used to indicate that while some object is not the only one that satisfies certain properties, all such objects are "the same" in some sense appropriate to the circumstances. This notion of "sameness" is often formalized using an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
A related notion is a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, where an object is not only essentially unique, but unique up to a unique isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
(meaning that it has trivial automorphism group). In general given two isomorphic examples of an essentially unique object, there is no natural (unique) isomorphism between them.
Set theory
Most basically, there is an essentially unique set of any given cardinality, whether one labels the elements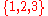 or
or 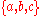 .
.In this case the non-uniqueness of the isomorphism (does one match 1 to a or to c?) is reflected in the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
On the other hand, there is an essentially unique ordered set of any given finite cardinality: if one writes
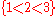 and
and 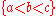 , then the only order-preserving isomorphism maps 1 to a, 2 to b, and 3 to c.
, then the only order-preserving isomorphism maps 1 to a, 2 to b, and 3 to c.Group theory
Suppose that we seek to classify all possible groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s. We would find that there is an essentially unique group containing exactly 3 elements, the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order three. No matter how we choose to write those three elements and denote the group operation, all such groups are isomorphic, hence, "the same".
On the other hand, there is not an essentially unique group with exactly 4 elements, as there are two non-isomorphic examples: the cyclic group of order 4 and the Klein four group.
Measure theory
Suppose that we seek a translation-invariantInvariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
, strictly positive
Strictly positive measure
In mathematics, strict positivity is a concept in measure theory. Intuitively, a strictly positive measure is one that is "nowhere zero", or that it is zero "only on points".-Definition:...
, locally finite measure
Locally finite measure
In mathematics, a locally finite measure is a measure for which every point of the measure space has a neighbourhood of finite measure.-Definition:...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. The solution to this problem is essentially unique: any such measure must be a constant multiple of Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. Specifying that the measure of the unit interval should be 1 then determines the solution uniquely.
Topology
Suppose that we seek to classify all two-dimensional, compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, simply connected manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. We would find an essentially unique solution to this problem: the 2-sphere. In this case, the solution is unique up to homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
Lie theory
A maximal compact subgroupMaximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of a semisimple Lie group may not be unique, but is unique up to conjugation.
See also
- Classification theoremClassification theoremIn mathematics, a classification theorem answers the classification problem "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class....
- Universal propertyUniversal propertyIn various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...

