The
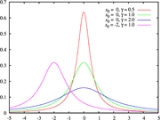
Cauchy–Lorentz distribution, named after Augustin Cauchy and
Hendrik LorentzHendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
, is a continuous
probability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. As a probability distribution, it is known as the
Cauchy distribution, while among physicists, it is known as the
Lorentz distribution,
Lorentz(ian) function, or
Breit–Wigner distribution.
Its importance in
physicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
is the result of its being the solution to the
differential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
describing forced resonance. In
mathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, it is closely related to the
Poisson kernelIn potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disc. The kernel can be understood as the derivative of the Green's function for the Laplace equation...
, which is the
fundamental solutionIn mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
for the Laplace equation in the
upper half-plane. In
spectroscopySpectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
, it is the description of the shape of
spectral lineA spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
s which are subject to
homogeneous broadeningHomogeneous broadening is a type of emission spectrum broadening in which all atoms radiating from a specific level under consideration radiate with equal opportunity. If an optical emitter Homogeneous broadening is a type of emission spectrum broadening in which all atoms radiating from a specific...
in which all atoms interact in the same way with the frequency range contained in the line shape. Many mechanisms cause homogeneous broadening, most notably collision broadening, and Chantler–Alda
radiationIn physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
. In its standard form, it is the
maximum entropy probability distributionIn statistics and information theory, a maximum entropy probability distribution is a probability distribution whose entropy is at least as great as that of all other members of a specified class of distributions....
for a random variate
X for which
.
Probability density function
The Cauchy distribution has the
probability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
where
is the
location parameterIn statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
, specifying the location of the peak of the distribution, and
is the
scale parameterIn probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
which specifies the half-width at half-maximum (HWHM).
is also equal to half the
interquartile rangeIn descriptive statistics, the interquartile range , also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles...
and is sometimes called the
probable error-Statistics:In statistics, the probable error of a quantity is a value describing the probability distribution of that quantity. It defines the half-range of an interval about a cental point for the distribution, such that half of the values from the distribution will lie within the interval and...
. Augustin-Louis Cauchy exploited such a density function in 1827 with an
infinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
scale parameter, defining what would now be called a
Dirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
The amplitude of the above Lorentzian function is given by
The special case when
and
is called the
standard Cauchy distribution with the probability density function
In physics, a three-parameter Lorentzian function is often used:
where
is the height of the peak.
Cumulative distribution function
The
cumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is:
and the
quantile functionIn probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
(inverse
cdfIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
) of the Cauchy distribution is
It follows that the first and third quartiles are
, and hence the
interquartile rangeIn descriptive statistics, the interquartile range , also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles...
is
.
The derivative of the
quantile functionIn probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
, the quantile density function, for the Cauchy distribution is:
The
differential entropyDifferential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
of a distribution can be defined in terms of its quantile density, specifically
Properties
The Cauchy distribution is an example of a distribution which has no
meanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
,
varianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
or higher
momentsIn mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
defined. Its
modeIn statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
and
medianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
are well defined and are both equal to x
0.
When
and
are two independent
normally distributed random variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s with
expected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and
varianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, then the ratio
has the standard Cauchy distribution.
If
are independent and identically distributed random variables, each with a standard Cauchy distribution, then the
sample meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
has the same standard Cauchy distribution (the sample median, which is not affected by extreme values, can be used as a measure of central tendency). To see that this is true, compute the
characteristic functionIn probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of the sample mean:
where
is the sample mean. This example serves to show that the hypothesis of finite variance in the
central limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
cannot be dropped. It is also an example of a more generalized version of the central limit theorem that is characteristic of all stable distributions, of which the Cauchy distribution is a special case.
The Cauchy distribution is an infinitely divisible probability distribution. It is also a strictly
stableIn probability theory, the stability of a random variable is the property that a linear combination of two independent copies of the variable has the same distribution, up to location and scale parameters. The distributions of random variables having this property are said to be "stable...
distribution.
The standard Cauchy distribution coincides with the
Student's t-distribution with one degree of freedom.
Like all stable distributions, the
location-scale familyIn probability theory, especially as that field is used in statistics, a location-scale family is a family of univariate probability distributions parametrized by a location parameter and a non-negative scale parameter; if X is any random variable whose probability distribution belongs to such a...
to which the Cauchy distribution belongs is closed under linear transformations with
realIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coefficients. In addition, the Cauchy distribution is the only univariate distribution which is closed under
linear fractional transformations with real coefficients. In this connection, see also
McCullagh's parametrization of the Cauchy distributions.
Characteristic function
Let
denote a Cauchy distributed random variable. The
characteristic functionIn probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of the Cauchy distribution is given by
which is just the
Fourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the probability density. The original probability density may be expressed in terms of the characteristic function, essentially by using the inverse Fourier transform:
Observe that the characteristic function is not differentiable at the origin: this corresponds to the fact that the Cauchy distribution does not have an
expected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
Mean
If a
probability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
has a
density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
f(
x), then the mean is
The question is now whether this is the same thing as
If at most one of the two terms in (2) is infinite, then (1) is the same as (2). But in the case of the Cauchy distribution, both the positive and negative terms of (2) are infinite. This means (2) is undefined. Moreover, if (1) is construed as a Lebesgue integral, then (1) is also undefined, because (1) is then defined simply as the difference (2) between positive and negative parts.
However, if (1) is construed as an
improper integralIn calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
rather than a Lebesgue integral, then (2) is undefined, and (1) is not necessarily
well-definedIn mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
. We may take (1) to mean
and this is its
Cauchy principal valueIn mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
, which is zero, but we could also take (1) to mean, for example,
which is
not zero, as can be seen easily by computing the integral.
Because the integrand is bounded and is not Lebesgue integrable, it is not even Henstock–Kurzweil integrable. Various results in probability theory about
expected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s, such as the strong law of large numbers, will not work in such cases.
Higher moments
The Cauchy distribution does not have moments of any order. This follows from
Hölder's inequalityIn mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
which implies that higher moments diverge if lower moments do. In particular, no second central moment exists, as can be verified by direct computation:
The variance does not exist because of the divergent mean, which is distinctly different from having an infinite variance.
Estimation of parameters
Because the mean and variance of the Cauchy distribution are not defined, attempts to estimate these parameters will not be successful. For example, if
N samples are taken from a Cauchy distribution, one may calculate the sample mean as:
Although the sample values
will be concentrated about the central value
, the sample mean will become increasingly variable as more samples are taken, because of the increased likelihood of encountering sample points with a large absolute value. In fact, the distribution of the sample mean will be equal to the distribution of the samples themselves; i.e., the sample mean of a large sample is no better (or worse) an estimator of
than any single observation from the sample. Similarly, calculating the sample variance will result in values that grow larger as more samples are taken.
Therefore, more robust means of estimating the central value
and the scaling parameter
are needed. One simple method is to take the median value of the sample as an estimator of
and half the sample
interquartile rangeIn descriptive statistics, the interquartile range , also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles...
as an estimator of
. Other, more precise and robust methods have been developed For example, the
truncated meanA truncated mean or trimmed mean is a statistical measure of central tendency, much like the mean and median. It involves the calculation of the mean after discarding given parts of a probability distribution or sample at the high and low end, and typically discarding an equal amount of both.For...
of the middle 24% of the sample order statistics produces an estimate for
that is more efficient than using either the sample median or the full sample mean. However, because of the fat tails of the Cauchy distribution, the efficiency of the estimator decreases if more than 24% of the sample is used.
Maximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
can also be used to estimate the parameters
and
. However, this tends to be complicated by the fact that this requires finding the roots of a high degree polynomial, and there can be multiple roots that represent local maxima. Also, while the maximum likelihood estimator is asymptotically efficient, it is relatively inefficient for small samples. The log-likelihood function for the Cauchy distribution for sample size n is:
Maximizing the log likelihood function with respect to
and
produces the following system of equations:
Note that
is a monotone function in
and that the solution
must satisfy
. Solving just for
requires solving a polynomial of degree 2
n − 1, and solving just for
requires solving a polynomial of degree
(first for
, then
). Therefore, whether solving for one parameter or for both paramters simultaneously, a
numericalNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
solution on a computer is typically required. The benefit of maximum likelihood estimation is asymptotic efficiency; estimating
using the sample median is only about 81% as asymptotically efficient as estimating
by maximum likelihood. The truncated sample mean using the middle 24% order statistics is about 88% as asymptotically efficient an estimator of
as the maximum likelihood estimate. When
Newton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
is used to find the solution for the maximum likelihood estimate, the middle 24% order statistics can be used as an initial solution for
.
Circular Cauchy distribution
If
X is Cauchy distributed with median
μ and scale parameter
γ, then the complex variable
has unit modulus and is distributed on the unit circle with density:
with respect to the angular variable
, where
and
expresses the two parameters of the associated linear Cauchy distribution for
x as a complex number:
The distribution
is called the circular Cauchy distribution
(also the complex Cauchy distribution) with parameter
. The circular Cauchy distribution is related to the
wrapped Cauchy distribution. If
is a wrapped Cauchy distribution with the parameter
representing the parameters of the corresponding "unwrapped" Cauchy distribution in the variable
y where
, then
See also
McCullagh's parametrization of the Cauchy distributions and
Poisson kernelIn potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disc. The kernel can be understood as the derivative of the Green's function for the Laplace equation...
for related concepts.
The circular Cauchy distribution expressed in complex form has finite moments of all orders
for integer
. For
, the transformation
is holomorphic on the unit disk, and the transformed variable
is distributed as complex Cauchy with parameter
.
Given a sample
of size
n > 2, the maximum-likelihood equation
can be solved by a simple fixed-point iteration:
starting with
The sequence of likelihood values is non-decreasing, and the solution is unique for samples containing at least three distinct values.
The maximum-likelihood estimate for the median (
) and scale parameter (
) of a real Cauchy sample is obtained by the inverse transformation:
For
n ≤ 4, closed-form expressions are known for
. The density of the maximum-likelihood estimator at
in the unit disk is necessarily of the form:
where
.
Formulae for
and
are available.
Multivariate Cauchy distribution
A random vector is said to have the multivariate Cauchy distribution if every linear combination of its components
Y =
a1X1 + ... +
akXk has a Cauchy distribution. That is, for any constant vector , the random variable should have a univariate Cauchy distribution. The characteristic function of a multivariate Cauchy distribution is given by:
where
and
are real functions with
a
homogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree one and
a positive homogeneous function of degree one. More formally:
and
for all
t.
An example of a bivariate Cauchy distribution can be given by:
Note that in this example, even though there is no analogue to a covariance matrix, x and y are not statistically independent.
Analogously to the univariate density, the multidimensional Cauchy density also relates to the
Multivariate Student distribution. They are equivalent when the degrees of freedom parameter is equal to one. The density of a k dimension Student distribution with one degree of freedom becomes:
Properties and details for this density can be obtained by taking it as a particular case of the Multivariate Student density.
Transformation properties
- If
then 
- If
then 
- If
and 
are independent, then 
- If
then 
- McCullagh's parametrization of the Cauchy distributions: Expressing a Cauchy distribution in terms of one complex parameter
, define to mean . If X ~ Cauchy
then:
~ Cauchy
where a,b,c and d are real numbers.
- Using the same convention as above, if If X ~ Cauchy
then:
~ CCauchy
- where "CCauchy" is the circular Cauchy distribution.
Related distributions
Relativistic Breit–Wigner distribution
In
nuclearNuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
and
particle physicsParticle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, the energy profile of a
resonanceIn physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
is described by the relativistic Breit–Wigner distribution, while the Cauchy distribution is the (non-relativistic) Breit–Wigner distribution.
External links