
Category of topological vector spaces
Encyclopedia
In mathematics
, the category of topological vector spaces is the category whose objects are topological vector space
s and whose morphism
s are continuous linear maps between them. This is a category because the composition
of two continuous linear maps is again continuous. The category is often denoted TVect or TVS.
Fixing a topological field K, one can also consider the (sub-)category TVectK of topological vector spaces over K with continuous K-linear maps as the morphisms.
, meaning its objects are sets with additional structure (i.e. a vector space structure and a topology) and its morphisms are functions
preserving this structure. There are obvious forgetful functor
s into the category of topological spaces
, the category of vector spaces
and the category of sets
.
The category is topological, which means loosely speaken that it relates to its "underlying category" the category of vector spaces in the same way that Top relates to Set. Formally:
For every single K-vector space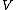 and every family
and every family 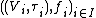 of topological K-vector spaces
of topological K-vector spaces  and K-linear maps
and K-linear maps 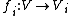 , there exists a vector space topology
, there exists a vector space topology  on
on 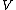 so that the following property is fulfilled:
so that the following property is fulfilled:
Whenever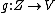 is a K-linear map from a topological K-vector space
is a K-linear map from a topological K-vector space 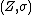 it holds:
it holds: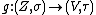 is continuous
is continuous 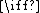
 is continuous.
is continuous.
The topological vector space is called "initial object" or "initial structure" with respect to the given data.
is called "initial object" or "initial structure" with respect to the given data.
If one replaces "vector space" by "set" and "linear map" by "map", one gets a characterisation of the usual initial topologies in Top. This is the reason why categories with this property are called "topological".
There are numerous consequences of this property. For example:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the category of topological vector spaces is the category whose objects are topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s and whose morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are continuous linear maps between them. This is a category because the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of two continuous linear maps is again continuous. The category is often denoted TVect or TVS.
Fixing a topological field K, one can also consider the (sub-)category TVectK of topological vector spaces over K with continuous K-linear maps as the morphisms.
TVect is a concrete category
Like many categories, the category TVect is a concrete categoryConcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
, meaning its objects are sets with additional structure (i.e. a vector space structure and a topology) and its morphisms are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
preserving this structure. There are obvious forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
s into the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, the category of vector spaces
Category of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
and the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
.
 is a topological category
is a topological category
The category is topological, which means loosely speaken that it relates to its "underlying category" the category of vector spaces in the same way that Top relates to Set. Formally:For every single K-vector space
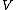 and every family
and every family 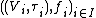 of topological K-vector spaces
of topological K-vector spaces  and K-linear maps
and K-linear maps 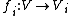 , there exists a vector space topology
, there exists a vector space topology  on
on 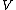 so that the following property is fulfilled:
so that the following property is fulfilled:Whenever
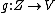 is a K-linear map from a topological K-vector space
is a K-linear map from a topological K-vector space 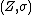 it holds:
it holds: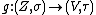 is continuous
is continuous 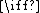
 is continuous.
is continuous.The topological vector space
 is called "initial object" or "initial structure" with respect to the given data.
is called "initial object" or "initial structure" with respect to the given data.If one replaces "vector space" by "set" and "linear map" by "map", one gets a characterisation of the usual initial topologies in Top. This is the reason why categories with this property are called "topological".
There are numerous consequences of this property. For example:
- "Discrete" and "indiscrete" objects exist. A topological vector space is indiscrete iff it is the initial structure with respect to the empty family. A topological vector space is discrete iff it is the initial structur with respect to the family of all possible linear maps into all topological vector spaces. (This family is a proper class, but in fact that doesn't matter: Initial structures with respect to all classes exists iff they exists with respect to all sets)
- Final structures (the similar defined analogue to final topologies) exist. But there is a catch: While the initial structure of the above property is in fact the usual initial topology on
 with respect to
with respect to 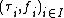 , the final structures don't need to be final with respect to given maps in the sense of Top. For example: The discrete objects (=final with respect to the empty family) in
, the final structures don't need to be final with respect to given maps in the sense of Top. For example: The discrete objects (=final with respect to the empty family) in  do not carry the discrete topology.
do not carry the discrete topology. - Since the following diagram of forgetful functors commutes
-

- and the forgetful functor from
 to Set is right adjoint, the forgetful functor from
to Set is right adjoint, the forgetful functor from  to Top is right adjoint too (and the correspondig left adjoints fit in an analogue commutative diagram). This left adjoint defines "free topological vector spaces". Explicitly these are free K-vector spaces equipped with a certain initial topology.
to Top is right adjoint too (and the correspondig left adjoints fit in an analogue commutative diagram). This left adjoint defines "free topological vector spaces". Explicitly these are free K-vector spaces equipped with a certain initial topology.
- Since
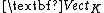 is (co)complete,
is (co)complete,  is (co)complete too.
is (co)complete too.
- Since
- and the forgetful functor from

