Concrete category
Encyclopedia
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets
. This functor makes it possible to think of the objects of the category as sets with additional structure
, and of its morphisms as structure-preserving functions. Many important categories have obvious interpretations as concrete categories, for example the category of topological spaces
and the category of groups
, and trivially also the category of sets itself. On the other hand, the homotopy category of topological spaces
is not concretizable, i.e. it does not admit a faithful functor to the category of sets.
A concrete category, when defined without reference to the notion of a category, consists of a class
of objects, each equipped with an underlying set; and for any two objects A and B a set of functions, called morphisms, from the underlying set of A to the underlying set of B. Furthermore, for every object A, the identity function on the underlying set of A must be a morphism from A to A, and the composition of a morphism from A to B followed by a morphism from B to C must be a morphism from A to C.
The functor U is to be thought of as a forgetful functor
, which assigns to every object of C its "underlying set", and to every morphism in C its "underlying function".
A category C is concretizable if there exists a concrete category (C,U);
i.e., if there exists a faithful functor U:C → Set. All small categories are concretizable: define U so that its object part maps each object b of C to the set of all morphisms of C whose codomain
is b (i.e. all morphisms of the form f: a → b for any object a of C), and its morphism part maps each morphism g: b → c of C to the function U(g): U(b) → U(c) which maps each member f: a → b of U(b) to the composition gf: a → c, a member of U(c). (Item 6 under Further examples expresses the same U in less elementary language via presheaves.) The Counter-examples section exhibits two large categories that are not concretizable.
which a category may or may not satisfy, but rather a structure with which a category may or may not be equipped. In particular, a category C may admit several faithful functors into Set. Hence there may be several concrete categories (C,U) all corresponding to the same category C.
In practice, however, the choice of faithful functor is often clear and in this case we simply speak of the "concrete category C". For example, "the concrete category Set" means the pair (Set,I) where I denotes the identity functor Set → Set.
The requirement that U be faithful means that it maps different morphisms between the same objects to different functions. However, U may map different objects to the same set and, if this occurs, it will also map different morphisms to the same function.
For example, if S and T are two different topologies on the same set X, then
(X,S) and (X,T) are distinct objects in the category Top of topological spaces and continuous maps, but mapped to the same set X by the forgetful functor Top → Set. Moreover, the identity morphism (X,S) → (X,S) and the identity morphism (X,T) → (X,T) are considered distinct morphisms in Top, but they have the same underlying function, namely the identity function on X.
Similarly, any set with 4 elements can be given two non-isomorphic group structures: one isomorphic to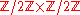
; the other isomorphic to 
.
, where the objects are topological space
s and the morphisms are homotopy classes
of continuous functions, is an example of a category that is not concretizable.
While the objects are sets (with additional structure), the morphisms are not actual functions between them, but rather classes of functions.
The fact that there does not exist any faithful functor from hTop to Set was first proven by Peter Freyd.
In the same article, Freyd cites an earlier result that the category of "small categories and natural equivalence-classes of functors" also fails to be concretizable.
N, let UN be the functor C → Set determined by UN(c) = (U(c))N.
Then a subfunctor
of UN is called an N-ary predicate and a
natural transformation
UN → U an N-ary operation.
The class of all N-ary predicates and N-ary operations of a concrete category (C,U), with N ranging over the class of all cardinal numbers, forms a large signature
. The category of models for this signature then contains a full subcategory which is equivalent
to C.
For this reason, it makes sense to call a pair (C,U) where C is a category and U a faithful functor C → X a concrete category over X.
For example, it may be useful to think of the models of a theory with N sorts as forming a concrete category over SetN.
In this context, a concrete category over Set is sometimes called a construct.
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. This functor makes it possible to think of the objects of the category as sets with additional structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
, and of its morphisms as structure-preserving functions. Many important categories have obvious interpretations as concrete categories, for example the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
and the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, and trivially also the category of sets itself. On the other hand, the homotopy category of topological spaces
Homotopy category of topological spaces
In mathematics, a homotopy category is a category whose objects are topological spaces and whose morphisms are homotopy classes of continuous functions. The homotopy category of all topological spaces is often denoted hTop or Toph....
is not concretizable, i.e. it does not admit a faithful functor to the category of sets.
A concrete category, when defined without reference to the notion of a category, consists of a class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of objects, each equipped with an underlying set; and for any two objects A and B a set of functions, called morphisms, from the underlying set of A to the underlying set of B. Furthermore, for every object A, the identity function on the underlying set of A must be a morphism from A to A, and the composition of a morphism from A to B followed by a morphism from B to C must be a morphism from A to C.
Definition
A concrete category is a pair (C,U) such that- C is a category, and
- U is a faithful functor C → Set (the category of sets and functions).
The functor U is to be thought of as a forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
, which assigns to every object of C its "underlying set", and to every morphism in C its "underlying function".
A category C is concretizable if there exists a concrete category (C,U);
i.e., if there exists a faithful functor U:C → Set. All small categories are concretizable: define U so that its object part maps each object b of C to the set of all morphisms of C whose codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
is b (i.e. all morphisms of the form f: a → b for any object a of C), and its morphism part maps each morphism g: b → c of C to the function U(g): U(b) → U(c) which maps each member f: a → b of U(b) to the composition gf: a → c, a member of U(c). (Item 6 under Further examples expresses the same U in less elementary language via presheaves.) The Counter-examples section exhibits two large categories that are not concretizable.
Remarks
It is important to note that, contrary to intuition, concreteness is not a propertyProperty (philosophy)
In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...
which a category may or may not satisfy, but rather a structure with which a category may or may not be equipped. In particular, a category C may admit several faithful functors into Set. Hence there may be several concrete categories (C,U) all corresponding to the same category C.
In practice, however, the choice of faithful functor is often clear and in this case we simply speak of the "concrete category C". For example, "the concrete category Set" means the pair (Set,I) where I denotes the identity functor Set → Set.
The requirement that U be faithful means that it maps different morphisms between the same objects to different functions. However, U may map different objects to the same set and, if this occurs, it will also map different morphisms to the same function.
For example, if S and T are two different topologies on the same set X, then
(X,S) and (X,T) are distinct objects in the category Top of topological spaces and continuous maps, but mapped to the same set X by the forgetful functor Top → Set. Moreover, the identity morphism (X,S) → (X,S) and the identity morphism (X,T) → (X,T) are considered distinct morphisms in Top, but they have the same underlying function, namely the identity function on X.
Similarly, any set with 4 elements can be given two non-isomorphic group structures: one isomorphic to
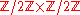; the other isomorphic to .Further examples
- Any group G may be regarded as an "abstract" category with one object,
, and one morphism for each element of the group. This would not be counted as concrete according to the intuitive notion described at the top of this article. But every faithful G-setGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
(equivalently, every representation of G as a group of permutationsPermutation groupIn mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
) determines a faithful functor G → Set. Since every group acts faithfully on itself, G can be made into a concrete category in at least one way. - Similarly, any poset P may be regarded as an abstract category with a unique arrow x → y whenever x ≤ y. This can be made concrete by defining a functor D : P → Set which maps each object x to
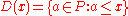and each arrow x → y to the inclusion map 
. - The category RelCategory of relationsIn mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.A morphism R : A → B in this category is a relation between the sets A and B, so ....
whose objects are sets and whose morphisms are relationsRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
can be made concrete by taking U to map each set X to its power set
and each relation 
to the function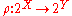 
defined by 
. Noting that power sets are complete latticeComplete latticeIn mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
s under inclusion, those functions between them arising from some relation R in this way are exactly the supremum-preserving maps. Hence Rel is equivalent to a full subcategory of the category Sup of complete lattices and their sup-preserving maps. Conversely, starting from this equivalence we can recover U as the composite Rel → Sup → Set of the forgetful functor for Sup with this embedding of Rel in Sup. - The category Setop can be embedded into Rel by representing each set as itself and each function f: X → Y as the relation from Y to X formed as the set of pairs (f(x),x) for all x ∈ X; hence Setop is concretizable. The forgetful functor which arises in this way is the contravariant powerset functor Setop → Set.
- It follows from the previous example that the opposite of any concretizable category C is again concretizable, since if U is a faithful functor C → Set then Cop may be equipped with the composite Cop → Setop → Set.
- If C is any small category, then there exists a faithful functor P : SetCop → Set which maps a presheaf X to the coproduct
. By composing this with the Yoneda embedding Y:C → SetCop one obtains a faithful functor C → Set. - For technical reasons, the category Ban1 of Banach spaces and linear contractionsContraction (operator theory)In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling...
is often equipped not with the "obvious" forgetful functor but the functor U1 : Ban1 → Set which maps a Banach space to its (closed) unit ball.
Counter-examples
The category hTopHomotopy category of topological spaces
In mathematics, a homotopy category is a category whose objects are topological spaces and whose morphisms are homotopy classes of continuous functions. The homotopy category of all topological spaces is often denoted hTop or Toph....
, where the objects are topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and the morphisms are homotopy classes
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
of continuous functions, is an example of a category that is not concretizable.
While the objects are sets (with additional structure), the morphisms are not actual functions between them, but rather classes of functions.
The fact that there does not exist any faithful functor from hTop to Set was first proven by Peter Freyd.
In the same article, Freyd cites an earlier result that the category of "small categories and natural equivalence-classes of functors" also fails to be concretizable.
Implicit structure of concrete categories
Given a concrete category (C,U) and a cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
N, let UN be the functor C → Set determined by UN(c) = (U(c))N.
Then a subfunctor
Subfunctor
In category theory, a branch of mathematics, a subfunctor is a special type of functor which is an analogue of a subset.-Definition:Let C be a category, and let F be a functor from C to the category of sets Set...
of UN is called an N-ary predicate and a
natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
UN → U an N-ary operation.
The class of all N-ary predicates and N-ary operations of a concrete category (C,U), with N ranging over the class of all cardinal numbers, forms a large signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
. The category of models for this signature then contains a full subcategory which is equivalent
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
to C.
Relative concreteness
In some parts of category theory, most notably topos theory, it is common to replace the category Set with a different category X, often called a base category.For this reason, it makes sense to call a pair (C,U) where C is a category and U a faithful functor C → X a concrete category over X.
For example, it may be useful to think of the models of a theory with N sorts as forming a concrete category over SetN.
In this context, a concrete category over Set is sometimes called a construct.