CHSH inequality
Encyclopedia
In physics
, the CHSH Bell test is an application of Bell's theorem
, intended to distinguish between the entanglement
hypothesis of quantum mechanics
and local hidden variable theories
. CHSH stands for John Clauser
, Michael Horne, Abner Shimony
and Richard Holt, who described it in a much-cited paper published in 1969 (Clauser et al, 1969). They derived the CHSH inequality, which, as with John Bell's
original one (Bell, 1964), applies to a statistical property of counts of "coincidences" in a Bell test experiment
that follows from the assumption that there exist underlying local hidden variables. The inequality must be obeyed under local realism but can be infringed under certain conditions in quantum mechanics.
(1) − 2 ≤ S ≤ 2,
(2) S = E(a, b) − E(a, b′) + E(a′, b) + E(a′ b′).
a and a′ are detector settings on side A, b and b′ on side B, the four combinations being tested in separate subexperiments. The terms E(a, b) etc. are the quantum correlation
s of the particle pairs, where the quantum correlation is defined to be the expectation value of the product of the "outcomes" of the experiment, i.e. the statistical average of A(a)·B(b), where A and B are the separate outcomes, using the coding +1 for the '+' channel and −1 for the '−' channel. Clauser et al.'s 1969 derivation was oriented towards the use of "two-channel" detectors, and indeed it is for these that it is generally used, but under their method the only possible outcomes were +1 and −1. In order to adapt it to real situations, which at the time meant the use of polarised light and single-channel polarisers, they had to interpret '−' as meaning "non-detection in the '+' channel", i.e. either '−' or nothing. They did not in the original article discuss how the two-channel inequality could be applied in real experiments with real imperfect detectors, though it was later proved (Bell, 1971) that the inequality itself was equally valid. The occurrence of zero outcomes, though, means it is no longer so obvious how the values of E are to be estimated from the experimental data.
The mathematical formalism of quantum mechanics predicts a maximum value for S of
, which is greater than 2, and CHSH violations are therefore predicted by the theory of quantum mechanics.
Note that in all actual Bell test experiments it is assumed that the source stays essentially constant, being characterised at any given instant by a state ("hidden variable") λ that has a constant distribution ρ(λ) and is unaffected by the choice of detector setting.
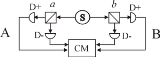
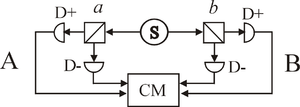In practice most actual experiments have used light rather than the electrons that Bell originally had in mind. The property of interest is, in the best known experiments (Aspect
, 1981-2), the polarisation direction, though other properties can be used. The diagram shows a typical optical experiment. Coincidences (simultaneous detections) are recorded, the results being categorised as '++', '+−', '−+' or '−−' and corresponding counts accumulated.
Four separate subexperiments are conducted, corresponding to the four terms E(a, b) in the test statistic S ((2) above). The settings a, a′, b and b′ are generally in practice chosen to be 0, 45°, 22.5° and 67.5° respectively — the "Bell test angles" — these being the ones for which the QM formula gives the greatest violation of the inequality.
For each selected value of a and b, the numbers of coincidences in each category (N++, N--, N+- and N-+) are recorded. The experimental estimate for E(a, b) is then calculated as:
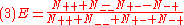
Once all the E’s have been estimated, an experimental estimate of S (expression (2)) can be found. If it is numerically greater than 2 it has infringed the CHSH inequality and the experiment is declared to have supported the QM (Quantum Mechanics
) prediction and ruled out all local hidden variable theories.
The CHSH paper lists many preconditions (or "reasonable and/or presumable assumptions") to derive the simplified theorem and formula. For example, for the method to be valid, it has to be assumed that the detected pairs are a fair sample of those emitted. In actual experiments, detectors are never 100% efficient, so that only a sample of the emitted pairs are detected. A subtle, related requirement is that the hidden variables do not influence or determine detection probability in a way that would lead to different samples at each arm of the experiment.
It would appear from both these later derivations that the only assumptions really needed for the inequality itself (as opposed to the method of estimation of the test statistic) are that the distribution of the possible states of the source remains constant and the detectors on the two sides act independently.
is itself a probability.
We start with the standard assumption of independence of the two sides, enabling us to obtain the joint probabilities of pairs of outcomes by multiplying the separate probabilities, for any selected value of the "hidden variable" λ. λ is assumed to be drawn from a fixed distribution of possible states of the source, the probability of the source being in the state λ for any particular trial being given by the density function ρ(λ), the integral of which over the complete hidden variable space is 1. We thus assume we can write:
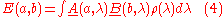
where A and B are the average values of the outcomes. Since the possible values of A and B are −1, 0 and +1, it follows that:
Then, if a, a′, b and b′ are alternative settings for the detectors,
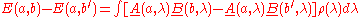
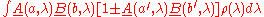
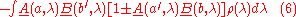
Then, applying the triangle inequality
to both sides, using (5) and the fact that
as well as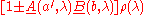 
are non-negative we obtain
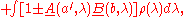
or, using the fact that the integral of ρ(λ) is 1,
which includes the CHSH inequality.
Working from the inhomogeneous version of the inequality, we can write:
(7) −1 ≤ pjk(a, b) − pjk(a, b′) + pjk(a′, b) + pjk(a′, b′) − pjk(a′) − pjk(b) ≤ 0,
where j and k are each '+' or '−', indicating which detectors are being considered.
To obtain the CHSH test statistic S (expression (2)), all that is needed is to multiply the inequalities for which j is different from k by −1 and add these to the inequalities for which j and k are the same.
second experiment in 1982 have used the CHSH inequality, estimating the terms using (3) and assuming fair sampling. Some dramatic violations of the inequality have been reported. Today, this formulation of the Bell inequality remains in use.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the CHSH Bell test is an application of Bell's theorem
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
, intended to distinguish between the entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
hypothesis of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and local hidden variable theories
Local hidden variable theory
In quantum mechanics, a local hidden variable theory is one in which distant events are assumed to have no instantaneous effect on local ones....
. CHSH stands for John Clauser
John Clauser
John Francis Clauser is an American theoretical and experimental physicist known for contributions to the foundations of quantum mechanics, in particular the Clauser-Horne-Shimony-Holt inequality....
, Michael Horne, Abner Shimony
Abner Shimony
Abner Shimony is an American physicist and philosopher of science specializing in quantum theory.-Career:Shimony obtained his BA in Mathematics and Philosophy from Yale University in 1948, and an MA in Philosophy from the University of Chicago in 1950. He obtained his Ph.D...
and Richard Holt, who described it in a much-cited paper published in 1969 (Clauser et al, 1969). They derived the CHSH inequality, which, as with John Bell's
John Stewart Bell
John Stewart Bell FRS was a British physicist from Northern Ireland , and the originator of Bell's theorem, a significant theorem in quantum physics regarding hidden variable theories.- Early life and work :...
original one (Bell, 1964), applies to a statistical property of counts of "coincidences" in a Bell test experiment
Bell test experiments
The Bell test experiments serve to investigate the validity of the entanglement effect in quantum mechanics by using some kind of Bell inequality...
that follows from the assumption that there exist underlying local hidden variables. The inequality must be obeyed under local realism but can be infringed under certain conditions in quantum mechanics.
Statement of the inequality
The usual form of the CHSH inequality is:(1) − 2 ≤ S ≤ 2,
- where
(2) S = E(a, b) − E(a, b′) + E(a′, b) + E(a′ b′).
a and a′ are detector settings on side A, b and b′ on side B, the four combinations being tested in separate subexperiments. The terms E(a, b) etc. are the quantum correlation
Quantum correlation
In Bell test experiments the term quantum correlation has come to mean the expectation value of the product of the outcomes on the two sides. In other words, the expected change in physical characteristics as one quantum system passes through an interaction site...
s of the particle pairs, where the quantum correlation is defined to be the expectation value of the product of the "outcomes" of the experiment, i.e. the statistical average of A(a)·B(b), where A and B are the separate outcomes, using the coding +1 for the '+' channel and −1 for the '−' channel. Clauser et al.'s 1969 derivation was oriented towards the use of "two-channel" detectors, and indeed it is for these that it is generally used, but under their method the only possible outcomes were +1 and −1. In order to adapt it to real situations, which at the time meant the use of polarised light and single-channel polarisers, they had to interpret '−' as meaning "non-detection in the '+' channel", i.e. either '−' or nothing. They did not in the original article discuss how the two-channel inequality could be applied in real experiments with real imperfect detectors, though it was later proved (Bell, 1971) that the inequality itself was equally valid. The occurrence of zero outcomes, though, means it is no longer so obvious how the values of E are to be estimated from the experimental data.
The mathematical formalism of quantum mechanics predicts a maximum value for S of
, which is greater than 2, and CHSH violations are therefore predicted by the theory of quantum mechanics.Note that in all actual Bell test experiments it is assumed that the source stays essentially constant, being characterised at any given instant by a state ("hidden variable") λ that has a constant distribution ρ(λ) and is unaffected by the choice of detector setting.
A typical CHSH experiment
Alain Aspect
Alain Aspect is a French physicist noted for his experimental work on quantum entanglement....
, 1981-2), the polarisation direction, though other properties can be used. The diagram shows a typical optical experiment. Coincidences (simultaneous detections) are recorded, the results being categorised as '++', '+−', '−+' or '−−' and corresponding counts accumulated.
Four separate subexperiments are conducted, corresponding to the four terms E(a, b) in the test statistic S ((2) above). The settings a, a′, b and b′ are generally in practice chosen to be 0, 45°, 22.5° and 67.5° respectively — the "Bell test angles" — these being the ones for which the QM formula gives the greatest violation of the inequality.
For each selected value of a and b, the numbers of coincidences in each category (N++, N--, N+- and N-+) are recorded. The experimental estimate for E(a, b) is then calculated as:
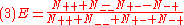
Once all the E’s have been estimated, an experimental estimate of S (expression (2)) can be found. If it is numerically greater than 2 it has infringed the CHSH inequality and the experiment is declared to have supported the QM (Quantum Mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
) prediction and ruled out all local hidden variable theories.
The CHSH paper lists many preconditions (or "reasonable and/or presumable assumptions") to derive the simplified theorem and formula. For example, for the method to be valid, it has to be assumed that the detected pairs are a fair sample of those emitted. In actual experiments, detectors are never 100% efficient, so that only a sample of the emitted pairs are detected. A subtle, related requirement is that the hidden variables do not influence or determine detection probability in a way that would lead to different samples at each arm of the experiment.
Derivation of the CHSH inequality
The original 1969 derivation will not be given here since it is not easy to follow and involves the assumption that the outcomes are all +1 or −1, never zero. Bell's 1971 derivation is more general. He effectively assumes the "Objective Local Theory" later used by Clauser and Horne (Clauser, 1974). It is assumed that any hidden variables associated with the detectors themselves are independent on the two sides and can be averaged out from the start. Another derivation of interest is given in Clauser and Horne's 1974 paper, in which they start from the CH74 inequality.It would appear from both these later derivations that the only assumptions really needed for the inequality itself (as opposed to the method of estimation of the test statistic) are that the distribution of the possible states of the source remains constant and the detectors on the two sides act independently.
Bell's 1971 derivation
The following is based on page 37 of Bell's Speakable and Unspeakable (Bell, 1971), the main change being to use the symbol ‘E’ instead of ‘P’ for the expected value of the quantum correlation. This avoids any implication that the quantum correlationQuantum correlation
In Bell test experiments the term quantum correlation has come to mean the expectation value of the product of the outcomes on the two sides. In other words, the expected change in physical characteristics as one quantum system passes through an interaction site...
is itself a probability.
We start with the standard assumption of independence of the two sides, enabling us to obtain the joint probabilities of pairs of outcomes by multiplying the separate probabilities, for any selected value of the "hidden variable" λ. λ is assumed to be drawn from a fixed distribution of possible states of the source, the probability of the source being in the state λ for any particular trial being given by the density function ρ(λ), the integral of which over the complete hidden variable space is 1. We thus assume we can write:
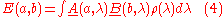
where A and B are the average values of the outcomes. Since the possible values of A and B are −1, 0 and +1, it follows that:
Then, if a, a′, b and b′ are alternative settings for the detectors,
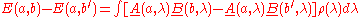
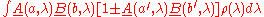
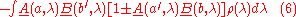
Then, applying the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
to both sides, using (5) and the fact that
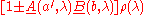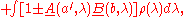
as well as are non-negative we obtainor, using the fact that the integral of ρ(λ) is 1,
which includes the CHSH inequality.
Derivation from Clauser and Horne's 1974 inequality
In their 1974 paper (Clauser, 1974), Clauser and Horne show that the CHSH inequality can be derived from the CH74 one. As they tell us, in a two-channel experiment the CH74 single-channel test is still applicable and provides four sets of inequalities governing the probabilities p of coincidences.Working from the inhomogeneous version of the inequality, we can write:
(7) −1 ≤ pjk(a, b) − pjk(a, b′) + pjk(a′, b) + pjk(a′, b′) − pjk(a′) − pjk(b) ≤ 0,
where j and k are each '+' or '−', indicating which detectors are being considered.
To obtain the CHSH test statistic S (expression (2)), all that is needed is to multiply the inequalities for which j is different from k by −1 and add these to the inequalities for which j and k are the same.
Experiments using the CHSH test
Many Bell test experiments conducted subsequent to Aspect'sAlain Aspect
Alain Aspect is a French physicist noted for his experimental work on quantum entanglement....
second experiment in 1982 have used the CHSH inequality, estimating the terms using (3) and assuming fair sampling. Some dramatic violations of the inequality have been reported. Today, this formulation of the Bell inequality remains in use.
See also
- Bell's TheoremBell's theoremIn theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
- Bell test experimentsBell test experimentsThe Bell test experiments serve to investigate the validity of the entanglement effect in quantum mechanics by using some kind of Bell inequality...
- Leggett–Garg inequality
- Quantum entanglementQuantum entanglementQuantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
- Quantum MechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...