Box topology
Encyclopedia
In topology
, the cartesian product
of topological space
s can be given several different topologies. The canonical one is the product topology
, because it fits rather nicely with the categorical
notion of a product
. Another possibility is the box topology. The box topology has a somewhat more obvious definition than the product topology, but it satisfies fewer desirable properties. In general, the box topology is finer than the product topology, although the two agree in the case of finite direct products (or when all but finitely many of the factors are trivial
).
,
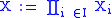or the (possibly infinite) Cartesian product of the topological spaces Xi, indexed
by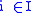
, the box topology on X is generated by B = { Π Ui | Ui open in Xi}. The name box comes from the case of Rn, the basis sets look like boxes or unions thereof. It is easily verified that B is actually a basis for the topology.
. Let Rω denote the countable cartesian product of R with itself, i.e. the set of all sequence
s in R. Let f : R → Rω be the product map whose components are all the identity, i.e. f(x) = (x, x, x, ...). Obviously the component functions are continuous. Consider the open set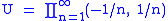
. If f were continuous, a preimage would have to contain an interval (−ε, ε) about 0 (since f(0) = (0,0,0,...) is in U). The image of this interval must, in turn, be contained in U. But the image of (−ε,ε) is its own countable cartesian product. But (−ε,ε) cannot be contained in (−1/n, 1/n) for every n; thus one concludes that f is not continuous even though all its components are.
S is precisely the space of functions from S to X; the product topology yields the topology of pointwise convergence
; sequences of functions converge
if and only if they converge at every point of S. The box topology, once again due to its great profusion of open sets, makes convergence very hard. One way to visualize the convergence in this topology is to think of functions from R to R — a sequence of functions converges to a function f in the box topology if, when looking at the graph of f, given any set of "hoops", that is, vertical open intervals surrounding the graph of f above every point on the x-axis, eventually, every function in the sequence "jumps through all the hoops." For functions on R this looks a lot like uniform convergence, in which case all the "hoops", once chosen, must be the same size. But in this case one can make the hoops arbitrarily small, so one can see intuitively how "hard" it is for sequences of functions to converge. The hoop picture works for convergence in the product topology as well: here we only require all the functions to jump through any given finite set of hoops. This stems directly from the fact that, in the product topology, almost all
the factors in a basic open set are the whole space. Interestingly, this is actually equivalent to requiring all functions to eventually jump through just a single given hoop; this is just the definition of pointwise convergence.
s — many qualities such as compactness
, connectedness
, metrizability, etc., if possessed by the factor spaces, are not in general preserved in the product with this topology.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s can be given several different topologies. The canonical one is the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, because it fits rather nicely with the categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
notion of a product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
. Another possibility is the box topology. The box topology has a somewhat more obvious definition than the product topology, but it satisfies fewer desirable properties. In general, the box topology is finer than the product topology, although the two agree in the case of finite direct products (or when all but finitely many of the factors are trivial
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
).
Definition
Given X such that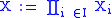,or the (possibly infinite) Cartesian product of the topological spaces Xi, indexed
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
by
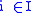, the box topology on X is generated by B = { Π Ui | Ui open in Xi}. The name box comes from the case of Rn, the basis sets look like boxes or unions thereof. It is easily verified that B is actually a basis for the topology.Properties
Box topology on Rω:- The box topology is completely regular
- The box topology is neither compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
nor connectedConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
- The box topology is not first countable
- Neither is the box topology separable
- The box topology is paracompact (and hence normal and completely regular) if the continuum hypothesisContinuum hypothesisIn mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
is true
Example
Here is an example given by Munkres, based on the Hilbert cubeHilbert cube
In mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology...
. Let Rω denote the countable cartesian product of R with itself, i.e. the set of all sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s in R. Let f : R → Rω be the product map whose components are all the identity, i.e. f(x) = (x, x, x, ...). Obviously the component functions are continuous. Consider the open set
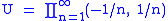. If f were continuous, a preimage would have to contain an interval (−ε, ε) about 0 (since f(0) = (0,0,0,...) is in U). The image of this interval must, in turn, be contained in U. But the image of (−ε,ε) is its own countable cartesian product. But (−ε,ε) cannot be contained in (−1/n, 1/n) for every n; thus one concludes that f is not continuous even though all its components are.Intuitive Description of Convergence; Comparisons
Topologies are often best understood by describing how sequences converge. In general, a cartesian product of a space X with itself over an indexing setIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
S is precisely the space of functions from S to X; the product topology yields the topology of pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
; sequences of functions converge
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
if and only if they converge at every point of S. The box topology, once again due to its great profusion of open sets, makes convergence very hard. One way to visualize the convergence in this topology is to think of functions from R to R — a sequence of functions converges to a function f in the box topology if, when looking at the graph of f, given any set of "hoops", that is, vertical open intervals surrounding the graph of f above every point on the x-axis, eventually, every function in the sequence "jumps through all the hoops." For functions on R this looks a lot like uniform convergence, in which case all the "hoops", once chosen, must be the same size. But in this case one can make the hoops arbitrarily small, so one can see intuitively how "hard" it is for sequences of functions to converge. The hoop picture works for convergence in the product topology as well: here we only require all the functions to jump through any given finite set of hoops. This stems directly from the fact that, in the product topology, almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
the factors in a basic open set are the whole space. Interestingly, this is actually equivalent to requiring all functions to eventually jump through just a single given hoop; this is just the definition of pointwise convergence.
Comparison with product topology
The basis sets in the product topology have almost the same definition as the above, except with the qualification that all but finitely many Ui are equal to the whole space Xi. The product topology satisfies a very desirable property for maps fi : Y → Xi into the component spaces: the product map f: Y → X defined by the component functions fi is continuous if and only if all the fi are continuous. This does not always hold in the box topology, because it is in general a much finer topology, so therefore mapping into the range space makes it much harder for functions to be continuous. This actually makes the box topology very useful for providing counterexampleCounterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
s — many qualities such as compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, connectedness
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, metrizability, etc., if possessed by the factor spaces, are not in general preserved in the product with this topology.