
Automorphisms of the symmetric and alternating groups
Encyclopedia
In group theory
, a branch of mathematics
, the automorphism
s and outer automorphisms of the symmetric group
s and alternating groups are both standard examples of these automorphisms, and objects of study in their own right, particularly the exceptional outer automorphism of S6, the symmetric group on 6 elements.
which one can call exceptional
(in analogy with exceptional Lie algebras) or exotic. In fact, Out(S6) = C2.
This was discovered by Otto Hölder
in 1895.
This also yields another outer automorphism of A6, and this is the only exceptional outer automorphism of a finite simple group: for the infinite families of simple groups, there are formulas for the number of outer automorphisms, and the simple group of order 360, thought of as A6, would be expected to have 2 outer automorphisms, not 4.
However, when A6 is viewed as PSL(2, 9) the outer automorphism group has the expected order. (For sporadic groups (not falling in an infinite family), the notion of exceptional outer automorphism is ill-defined, as there is no general formula.)
Note that as an outer automorphism, it's a class of automorphisms, well-determined only up to an inner automorphism, hence there is not a natural one to write down.
One method is:
Throughout the following, one can work with the multiplication action on cosets or the conjugation action on conjugates.
To see that S6 has an outer automorphism, recall that homomorphisms
from a group G to a symmetric group Sn are essentially the same as actions
of G on a set of n elements, and the subgroup fixing a point is then a subgroup of index
at most n in G. Conversely if we have a subgroup of index n in G, the action on the cosets gives a transitive action of G on n points, and therefore a homomorphism to Sn.
This follows from inspection of 5-cycles: each 5-cycle generates a group of order 5 (thus a Sylow subgroup), there are 5!/5 = 120/5 = 24 5-cycles, yielding 6 subgroups (as each subgroup also includes the identity), and Sn acts transitively by conjugation on cycles of a given class, hence transitively by conjugation on these subgroups.
One can also use the Sylow theorems, which imply transitivity.
of dimension two over the finite field
with five elements, PGL(2, 5), acts on the projective line
over the field with five elements, P1(F5), which has six elements. Further, this action is faithful and 3-transitive, as is always the case for the action of the projective linear group on the projective line. This yields a map PGL(2, 5) → S6 as a transitive subgroup. Identifying PGL(2, 5) with S5 and the projective special linear group PSL(2, 5) with A5 yields the desired exotic maps S5 → S6 and A5 → A6.
Following the same philosophy, one can realize the outer automorphism as the following two inequivalent actions of S6 on a set with six elements:
To construct an outer automorphism of S6, we need to construct
an "unusual" subgroup of index 6 in S6, in other words one that is not one of the six obvious S5 subgroups fixing a point (which just correspond to inner automorphisms of S6).
The Frobenius group
of affine transformation
s of F5
(maps x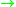 ax + b where a ≠ 0) has order 20 = (5 − 1) · 5 and acts on the field with 5 elements, hence is a subgroup of S5.
ax + b where a ≠ 0) has order 20 = (5 − 1) · 5 and acts on the field with 5 elements, hence is a subgroup of S5.
(Indeed, it is the normalizer of a Sylow 5-group mentioned above, thought of as the order-5 group of translations of F5.)
S5 acts transitively on the coset space, which is a set of 120/20 = 6 elements (or by conjugation, which yields the action above).
found a copy of Aut(S6) in the Mathieu group
M12 (a subgroup T isomorphic to S6 and an element σ that normalizes T and acts by outer automorphism). Similarly to S6 acting on a set of 6 elements in 2 different ways (having an outer automorphism), M12 acts on a set of 12 elements in 2 different ways (has an outer automorphism), though since M12 is itself exceptional, one does not consider this outer automorphism to be exceptional itself.
The full automorphism group of A6 appears naturally as a maximal subgroup of the Mathieu group M12 in 2 ways, as either a subgroup fixing a division of the 12 points into a pair of 6-element sets, or as a subgroup fixing a subset of 2 points.
Another way to see that S6 has a nontrivial outer automorphism is to use the fact that A6 is isomorphic to PSL2(9), whose automorphism group is the projective semilinear group PΓL2(9), in which PSL2(9) is index 4, yielding an outer automorphism group of order 4. The most visual way to see this automorphism is to give an interpretation via algebraic geometry over finite fields, as follows. Consider the action of S6 on affine 6-space over the field k with 3 elements. This action preserves several things: the hyperplane H on which the coordinates sum to 0, the line L in H where all coordinates coincide, and the quadratic form q given by the sum of the squares of all 6 coordinates. The restriction of q to H has defect line L, so there is an induced quadratic form Q on the 4-dimensional H/L that one checks is non-degenerate and non-split. The zero scheme of Q in H/L defines a smooth quadric surface X in the associated projective 3-space over k. Over an algebraic closure of k, X is a product of two projective lines, so by a descent argument X is the Weil restriction to k of the projective line over a quadratic etale algebra K. Since Q is not split over k, an auxiliary argument with special orthogonal groups over k forces K to be a field (rather than a product of two copies of k). The natural S6-action on everything in sight defines a map from S6 to the k-automorphism group of X, which is the semi-direct product G of PGL2(K) = PGL2(9) against
the Galois involution. This map carries the simple group A6 nontrivially into (hence onto) the subgroup PSL2(9) of index 4 in the semi-direct product G, so S6 is thereby identified as an index-2 subgroup of G (namely, the unique such subgroup distinct from PGL2(9) that also does not contain the Galois involution). Conjugation by any element of G outside of S6defines the nontrivial outer automorphism of S6.
On A6, it interchanges the 3-cycles (like (123)) with elements of class 32 (like (123)(456)).
This latter can be shown in two ways:
If one forms the products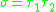 of two different transpositions
of two different transpositions 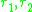 then one obtains either a 3-cycle or a permutation of type 1n−422. In particular the order of the produced elements is either two or three. On the other hand if one forms products
then one obtains either a 3-cycle or a permutation of type 1n−422. In particular the order of the produced elements is either two or three. On the other hand if one forms products 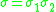 of involutions
of involutions 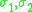 each consisting of k ≥ 2 2-cycles it may happen (for n ≥ 7) that the product contains either
each consisting of k ≥ 2 2-cycles it may happen (for n ≥ 7) that the product contains either
Note here that any 7-cycle in S7 is the product of two involutions of class 11 23, any permutation of class 42 in S8 is a product of involutions of class 24, finally a permutation of class 2231 in S7 is a product of two involutions of class 13 22 (for larger k resp. larger n compose these permutations with redundant 2-cycles or fixed points acting on the complement of a 7-element subset or 8-element subset such that they cancel out in the product). Now one arrives at a contradiction because the automorphism f must preserve the order (which is either two or three) of elements given as the product of the images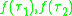 under f of two different transpositions, an order divisible by 7, 4 or 6 therefore cannot occur.
under f of two different transpositions, an order divisible by 7, 4 or 6 therefore cannot occur.
To see this, observe that there are only two conjugacy classes of S6 of order 15: the transpositions and those of class 23. Thus Aut(S6) acts on these two conjugacy classes (and the outer automorphism above interchanges these conjugacy classes), and an index 2 subgroup stabilizes the transpositions. But an automorphism that stabilizes the transpositions is inner, so the inner automorphisms are an index 2 subgroup of Aut(S6), so Out(S6) = C2.
More pithily: an automorphism that stabilizes transpositions is inner, and there are only two conjugacy classes of order 15 (transpositions and triple transpositions), hence the outer automorphism group is at most order 2.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s and outer automorphisms of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s and alternating groups are both standard examples of these automorphisms, and objects of study in their own right, particularly the exceptional outer automorphism of S6, the symmetric group on 6 elements.
Summary
| n | 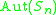 |
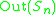 |
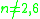 |
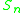 |
1 |
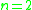 |
1 | 1 |
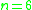 |
 |
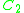 |
| n | 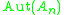 |
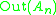 |
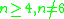 |
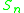 |
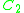 |
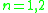 |
1 | 1 |
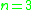 |
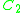 |
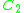 |
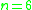 |
 |
 Klein four-group In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2... |
Generic case
-
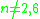 :
: 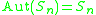 , and thus
, and thus 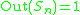 .
.
- Formally,
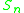 is completeComplete groupIn mathematics, a group G is said to be complete if every automorphism of G is inner, and the group is a centerless group; that is, it has a trivial outer automorphism group and trivial center....
is completeComplete groupIn mathematics, a group G is said to be complete if every automorphism of G is inner, and the group is a centerless group; that is, it has a trivial outer automorphism group and trivial center....
and the natural map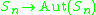 is an isomorphism.
is an isomorphism.
-
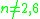 :
: 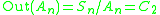 , and the outer automorphism is conjugation by an odd permutationEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
, and the outer automorphism is conjugation by an odd permutationEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
. -
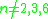 :
: 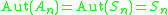
-
- Formally, the natural maps
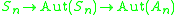 are isomorphisms.
are isomorphisms.
Exceptional cases
-
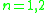 : trivial:
: trivial: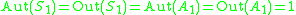
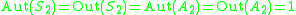
-
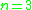 :
: 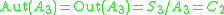
-
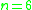 :
: 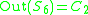 , and
, and 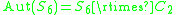 is a semidirect productSemidirect productIn mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
is a semidirect productSemidirect productIn mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
. -
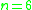 :
: 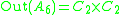 , and
, and 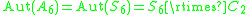 .
.
The exceptional outer automorphism of S6
Among symmetric groups, only S6 has a (non-trivial) outer automorphism,which one can call exceptional
Exceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
(in analogy with exceptional Lie algebras) or exotic. In fact, Out(S6) = C2.
This was discovered by Otto Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
in 1895.
This also yields another outer automorphism of A6, and this is the only exceptional outer automorphism of a finite simple group: for the infinite families of simple groups, there are formulas for the number of outer automorphisms, and the simple group of order 360, thought of as A6, would be expected to have 2 outer automorphisms, not 4.
However, when A6 is viewed as PSL(2, 9) the outer automorphism group has the expected order. (For sporadic groups (not falling in an infinite family), the notion of exceptional outer automorphism is ill-defined, as there is no general formula.)
Construction
There are numerous constructions, listed in .Note that as an outer automorphism, it's a class of automorphisms, well-determined only up to an inner automorphism, hence there is not a natural one to write down.
One method is:
- Construct an exotic map (embedding) S5 → S6
- S6 acts by conjugation on the six conjugates of this subgroup;
- yielding a map S6 → SX, where X is the set of conjugates. Identifying X with the numbers 1, ..., 6 (which depends on a choice of numbering of the conjugates, i.e., up to an element of S6 (an inner automorphism)) yields an outer automorphism S6 → S6.
- This map is an outer automorphism, since a transposition doesn't map to a transposition, but inner automorphisms preserve cycle structure.
Throughout the following, one can work with the multiplication action on cosets or the conjugation action on conjugates.
To see that S6 has an outer automorphism, recall that homomorphisms
from a group G to a symmetric group Sn are essentially the same as actions
of G on a set of n elements, and the subgroup fixing a point is then a subgroup of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
at most n in G. Conversely if we have a subgroup of index n in G, the action on the cosets gives a transitive action of G on n points, and therefore a homomorphism to Sn.
Exotic map S5 → S6
There is a subgroup (indeed, 6 conjugate subgroups) of S6 which are abstractly isomorphic to S5, and transitive as subgroups of S6.Sylow 5-subgroups
Janusz and Rotman construct it thus:- S5 acts transitively by conjugation on its 6 Sylow 5-subgroups, yielding an embedding S5 → S6 as a transitive subgroup of order 120. (The obvious map Sn → Sn+1 fixes a point and thus isn't transitive.)
This follows from inspection of 5-cycles: each 5-cycle generates a group of order 5 (thus a Sylow subgroup), there are 5!/5 = 120/5 = 24 5-cycles, yielding 6 subgroups (as each subgroup also includes the identity), and Sn acts transitively by conjugation on cycles of a given class, hence transitively by conjugation on these subgroups.
One can also use the Sylow theorems, which imply transitivity.
PGL(2,5)
The projective linear groupProjective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
of dimension two over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with five elements, PGL(2, 5), acts on the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
over the field with five elements, P1(F5), which has six elements. Further, this action is faithful and 3-transitive, as is always the case for the action of the projective linear group on the projective line. This yields a map PGL(2, 5) → S6 as a transitive subgroup. Identifying PGL(2, 5) with S5 and the projective special linear group PSL(2, 5) with A5 yields the desired exotic maps S5 → S6 and A5 → A6.
Following the same philosophy, one can realize the outer automorphism as the following two inequivalent actions of S6 on a set with six elements:
- the usual action as a permutation group;
- the six inequivalent structures as the projective line P1(F5) – the line has 6 points, and the projective linear group acts 3-transitively, so fixing 3 of the points, there are 3! = 6 different ways to arrange the remaining 3 points, which yields the desired alternative action.
Frobenius group
Another way:To construct an outer automorphism of S6, we need to construct
an "unusual" subgroup of index 6 in S6, in other words one that is not one of the six obvious S5 subgroups fixing a point (which just correspond to inner automorphisms of S6).
The Frobenius group
Frobenius group
In mathematics, a Frobenius group is a transitive permutation group on a finite set, such that no non-trivial elementfixes more than one point and some non-trivial element fixes a point.They are named after F. G. Frobenius.- Structure :...
of affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s of F5
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
(maps x
 ax + b where a ≠ 0) has order 20 = (5 − 1) · 5 and acts on the field with 5 elements, hence is a subgroup of S5.
ax + b where a ≠ 0) has order 20 = (5 − 1) · 5 and acts on the field with 5 elements, hence is a subgroup of S5.(Indeed, it is the normalizer of a Sylow 5-group mentioned above, thought of as the order-5 group of translations of F5.)
S5 acts transitively on the coset space, which is a set of 120/20 = 6 elements (or by conjugation, which yields the action above).
Other constructions
Ernst WittErnst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
found a copy of Aut(S6) in the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M12 (a subgroup T isomorphic to S6 and an element σ that normalizes T and acts by outer automorphism). Similarly to S6 acting on a set of 6 elements in 2 different ways (having an outer automorphism), M12 acts on a set of 12 elements in 2 different ways (has an outer automorphism), though since M12 is itself exceptional, one does not consider this outer automorphism to be exceptional itself.
The full automorphism group of A6 appears naturally as a maximal subgroup of the Mathieu group M12 in 2 ways, as either a subgroup fixing a division of the 12 points into a pair of 6-element sets, or as a subgroup fixing a subset of 2 points.
Another way to see that S6 has a nontrivial outer automorphism is to use the fact that A6 is isomorphic to PSL2(9), whose automorphism group is the projective semilinear group PΓL2(9), in which PSL2(9) is index 4, yielding an outer automorphism group of order 4. The most visual way to see this automorphism is to give an interpretation via algebraic geometry over finite fields, as follows. Consider the action of S6 on affine 6-space over the field k with 3 elements. This action preserves several things: the hyperplane H on which the coordinates sum to 0, the line L in H where all coordinates coincide, and the quadratic form q given by the sum of the squares of all 6 coordinates. The restriction of q to H has defect line L, so there is an induced quadratic form Q on the 4-dimensional H/L that one checks is non-degenerate and non-split. The zero scheme of Q in H/L defines a smooth quadric surface X in the associated projective 3-space over k. Over an algebraic closure of k, X is a product of two projective lines, so by a descent argument X is the Weil restriction to k of the projective line over a quadratic etale algebra K. Since Q is not split over k, an auxiliary argument with special orthogonal groups over k forces K to be a field (rather than a product of two copies of k). The natural S6-action on everything in sight defines a map from S6 to the k-automorphism group of X, which is the semi-direct product G of PGL2(K) = PGL2(9) against
the Galois involution. This map carries the simple group A6 nontrivially into (hence onto) the subgroup PSL2(9) of index 4 in the semi-direct product G, so S6 is thereby identified as an index-2 subgroup of G (namely, the unique such subgroup distinct from PGL2(9) that also does not contain the Galois involution). Conjugation by any element of G outside of S6defines the nontrivial outer automorphism of S6.
Structure of outer automorphism
On cycles, it exchanges permutations of type (12) with (12)(34)(56) (class 21 with class 23), and of type (123) with (145)(263) (class 31 with class 32).On A6, it interchanges the 3-cycles (like (123)) with elements of class 32 (like (123)(456)).
No other outer automorphisms
To see that none of the other symmetric groups have outer automorphisms, it is easiest to proceed in two steps:- First, show that any automorphism that preserves the conjugacy classConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
of transpositions is an inner automorphism. (This also shows that the outer automorphism of S6 is unique; see below.) - Second, show that every automorphism (other than the above for S6) stabilizes transpositions.
This latter can be shown in two ways:
- For every symmetric group other than S6, there is no other conjugacy class of elements of order 2 with the same number of elements as the class of transpositions.
- Or as follows:
If one forms the products
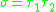 of two different transpositions
of two different transpositions 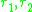 then one obtains either a 3-cycle or a permutation of type 1n−422. In particular the order of the produced elements is either two or three. On the other hand if one forms products
then one obtains either a 3-cycle or a permutation of type 1n−422. In particular the order of the produced elements is either two or three. On the other hand if one forms products 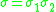 of involutions
of involutions 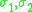 each consisting of k ≥ 2 2-cycles it may happen (for n ≥ 7) that the product contains either
each consisting of k ≥ 2 2-cycles it may happen (for n ≥ 7) that the product contains either
- a 7-cycle
- two 4-cycles
- a 2-cycle and a 3-cycle
Note here that any 7-cycle in S7 is the product of two involutions of class 11 23, any permutation of class 42 in S8 is a product of involutions of class 24, finally a permutation of class 2231 in S7 is a product of two involutions of class 13 22 (for larger k resp. larger n compose these permutations with redundant 2-cycles or fixed points acting on the complement of a 7-element subset or 8-element subset such that they cancel out in the product). Now one arrives at a contradiction because the automorphism f must preserve the order (which is either two or three) of elements given as the product of the images
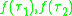 under f of two different transpositions, an order divisible by 7, 4 or 6 therefore cannot occur.
under f of two different transpositions, an order divisible by 7, 4 or 6 therefore cannot occur.No other outer automorphisms of S6
S6 has exactly one (class) of outer automorphisms: Out(S6 ) = C2.To see this, observe that there are only two conjugacy classes of S6 of order 15: the transpositions and those of class 23. Thus Aut(S6) acts on these two conjugacy classes (and the outer automorphism above interchanges these conjugacy classes), and an index 2 subgroup stabilizes the transpositions. But an automorphism that stabilizes the transpositions is inner, so the inner automorphisms are an index 2 subgroup of Aut(S6), so Out(S6) = C2.
More pithily: an automorphism that stabilizes transpositions is inner, and there are only two conjugacy classes of order 15 (transpositions and triple transpositions), hence the outer automorphism group is at most order 2.

