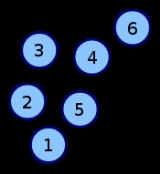
Adjacency matrix
Encyclopedia
In mathematics
and computer science
, an adjacency matrix is a means of representing which vertices
(or nodes) of a graph
are adjacent to which other vertices. Another matrix representation for a graph is the incidence matrix
.
Specifically, the adjacency matrix of a finite graph G on n vertices is the n × n matrix where the non-diagonal entry aij is the number of edges from vertex i to vertex j, and the diagonal entry aii, depending on the convention, is either once or twice the number of edges (loops) from vertex i to itself. Undirected graphs often use the latter convention of counting loops twice, whereas directed graphs typically use the former convention. There exists a unique adjacency matrix for each isomorphism class of graphs (up to permuting rows and columns), and it is not the adjacency matrix of any other isomorphism class of graphs. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected, the adjacency matrix is symmetric.
The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory
.
whose parts have r and s vertices has the form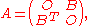
where B is an r × s matrix and O is an all-zero matrix. Clearly, the matrix B uniquely represents the bipartite graphs. It is sometimes called the biadjacency matrix.
Formally, let G = (U, V, E) be a bipartite graph
with parts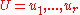 and
and  . The biadjacency matrix is the r x s 0-1 matrix B in which
. The biadjacency matrix is the r x s 0-1 matrix B in which 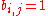 iff
iff
 .
.
If G is a bipartite multigraph
or weighted graph then the elements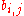 are taken to be the number of edges between the vertices or the weight of the edge
are taken to be the number of edges between the vertices or the weight of the edge 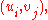 respectively.
respectively.
eigenvalues and an orthogonal eigenvector basis. The set of eigenvalues of a graph is the spectrum of the graph.
Suppose two directed or undirected graphs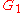 and
and  with adjacency matrices
with adjacency matrices  and
and 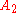 are given.
are given. 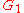 and
and 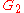 are isomorphic
are isomorphic
if and only if there exists a permutation matrix
 such that
such that
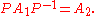
In particular, and
and 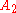 are similar and therefore have the same minimal polynomial, characteristic polynomial
are similar and therefore have the same minimal polynomial, characteristic polynomial
, eigenvalues, determinant
and trace. These can therefore serve as isomorphism invariants of graphs. However, two graphs may possess the same set of eigenvalues but not be isomorphic.
If A is the adjacency matrix of the directed or undirected graph G, then the matrix An (i.e., the matrix product
of n copies of A) has an interesting interpretation: the entry in row i and column j gives the number of (directed or undirected) walks of length n from vertex i to vertex j. This implies, for example, that the number of triangles in an undirected graph G is exactly the trace
of A3 divided by 6.
The main diagonal of every adjacency matrix corresponding to a graph without loops has all zero entries.
For -regular graphs, d is also an eigenvalue of A for the vector
-regular graphs, d is also an eigenvalue of A for the vector  , and
, and  is connected if and only if the multiplicity of
is connected if and only if the multiplicity of  is 1. It can be shown that
is 1. It can be shown that  is also an eigenvalue of A if G is a connected bipartite graph
is also an eigenvalue of A if G is a connected bipartite graph
. The above are results of Perron–Frobenius theorem
.
is a (−1,1,0)-adjacency matrix. This matrix is used in studying strongly regular graph
s and two-graph
s.
The distance matrix
has in position (i,j) the distance between vertices vi and vj . The distance is the length of a shortest path connecting the vertices. Unless lengths of edges are explicitly provided, the length of a path is the number of edges in it. The distance matrix resembles a high power of the adjacency matrix, but instead of telling only whether or not two vertices are connected, it gives the exact distance between them.
, the main alternative to the adjacency matrix is the adjacency list
. Because each entry in the adjacency matrix requires only one bit, it can be represented in a very compact way, occupying only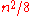 bytes of contiguous space, where
bytes of contiguous space, where  is the number of vertices. Besides avoiding wasted space, this compactness encourages locality of reference
is the number of vertices. Besides avoiding wasted space, this compactness encourages locality of reference
.
In contrast, for a sparse graph adjacency lists win out, because they use no space to represent edges that are not present. Using a naïve array implementation on a 32-bit computer, an adjacency list for an undirected graph requires about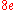 bytes of storage, where
bytes of storage, where  is the number of edges.
is the number of edges.
Noting that a simple graph can have at most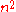 edges, allowing loops, we can let
edges, allowing loops, we can let 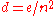 denote the density of the graph. Then,
denote the density of the graph. Then,  , or the adjacency list representation occupies more space precisely when
, or the adjacency list representation occupies more space precisely when  . Thus a graph must be sparse indeed to justify an adjacency list representation.
. Thus a graph must be sparse indeed to justify an adjacency list representation.
Besides the space tradeoff, the different data structures also facilitate different operations. Finding all vertices adjacent to a given vertex in an adjacency list is as simple as reading the list. With an adjacency matrix, an entire row must instead be scanned, which takes O
(n) time. Whether there is an edge between two given vertices can be determined at once with an adjacency matrix, while requiring time proportional to the minimum degree of the two vertices with the adjacency list.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, an adjacency matrix is a means of representing which vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
(or nodes) of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
are adjacent to which other vertices. Another matrix representation for a graph is the incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
.
Specifically, the adjacency matrix of a finite graph G on n vertices is the n × n matrix where the non-diagonal entry aij is the number of edges from vertex i to vertex j, and the diagonal entry aii, depending on the convention, is either once or twice the number of edges (loops) from vertex i to itself. Undirected graphs often use the latter convention of counting loops twice, whereas directed graphs typically use the former convention. There exists a unique adjacency matrix for each isomorphism class of graphs (up to permuting rows and columns), and it is not the adjacency matrix of any other isomorphism class of graphs. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected, the adjacency matrix is symmetric.
The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
.
Examples
The convention followed here is that an adjacent edge counts 1 in the matrix for an undirected graph.| Labeled graph | Adjacency matrix |
|---|---|
 |
 Coordinates are 1-6. |
The Nauru graph Nauru graph In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.... |
Coordinates are 0-23. White fields are zeros, colored fields are ones. |
Directed Directed graph A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,... Cayley graph Cayley graph In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group... of S Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... 4 |
As the graph is directed, the matrix is not symmetric. |
- The adjacency matrix of a complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
is all 1's except for 0's on the diagonal. - The adjacency matrix of an empty graph is a zero matrix.
Adjacency matrix of a bipartite graph
The adjacency matrix A of a bipartite graphBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
whose parts have r and s vertices has the form
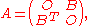
where B is an r × s matrix and O is an all-zero matrix. Clearly, the matrix B uniquely represents the bipartite graphs. It is sometimes called the biadjacency matrix.
Formally, let G = (U, V, E) be a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
with parts
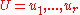 and
and  . The biadjacency matrix is the r x s 0-1 matrix B in which
. The biadjacency matrix is the r x s 0-1 matrix B in which 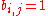 iff
iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
 .
.If G is a bipartite multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
or weighted graph then the elements
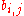 are taken to be the number of edges between the vertices or the weight of the edge
are taken to be the number of edges between the vertices or the weight of the edge 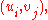 respectively.
respectively.Properties
The adjacency matrix of an undirected simple graph is symmetric, and therefore has a complete set of realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
eigenvalues and an orthogonal eigenvector basis. The set of eigenvalues of a graph is the spectrum of the graph.
Suppose two directed or undirected graphs
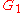 and
and  with adjacency matrices
with adjacency matrices  and
and 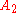 are given.
are given. 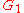 and
and 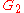 are isomorphic
are isomorphicGraph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
if and only if there exists a permutation matrix
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
 such that
such that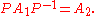
In particular,
 and
and 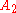 are similar and therefore have the same minimal polynomial, characteristic polynomial
are similar and therefore have the same minimal polynomial, characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
, eigenvalues, determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and trace. These can therefore serve as isomorphism invariants of graphs. However, two graphs may possess the same set of eigenvalues but not be isomorphic.
If A is the adjacency matrix of the directed or undirected graph G, then the matrix An (i.e., the matrix product
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of n copies of A) has an interesting interpretation: the entry in row i and column j gives the number of (directed or undirected) walks of length n from vertex i to vertex j. This implies, for example, that the number of triangles in an undirected graph G is exactly the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of A3 divided by 6.
The main diagonal of every adjacency matrix corresponding to a graph without loops has all zero entries.
For
 -regular graphs, d is also an eigenvalue of A for the vector
-regular graphs, d is also an eigenvalue of A for the vector  , and
, and  is connected if and only if the multiplicity of
is connected if and only if the multiplicity of  is 1. It can be shown that
is 1. It can be shown that  is also an eigenvalue of A if G is a connected bipartite graph
is also an eigenvalue of A if G is a connected bipartite graphBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
. The above are results of Perron–Frobenius theorem
Perron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
.
Variations
An (a, b, c)-adjacency matrix A of a simple graph has Aij = a if ij is an edge, b if it is not, and c on the diagonal. The Seidel adjacency matrixSeidel adjacency matrix
In mathematics, in graph theory, the Seidel adjacency matrix of a simple graph G is the symmetric matrix with a row and column for each vertex, having 0 on the diagonal and, in the positions corresponding to vertices vi and vj, −1 if the vertices are adjacent...
is a (−1,1,0)-adjacency matrix. This matrix is used in studying strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
s and two-graph
Two-graph
In mathematics, a two-graph is a set of triples chosen from a finite vertex set X, such that every quadruple from X contains an even number of triples of the two-graph. A regular two-graph has the property that every pair of vertices lies in the same number of triples of the two-graph...
s.
The distance matrix
Distance matrix
In mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points...
has in position (i,j) the distance between vertices vi and vj . The distance is the length of a shortest path connecting the vertices. Unless lengths of edges are explicitly provided, the length of a path is the number of edges in it. The distance matrix resembles a high power of the adjacency matrix, but instead of telling only whether or not two vertices are connected, it gives the exact distance between them.
Data structures
For use as a data structureData structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
, the main alternative to the adjacency matrix is the adjacency list
Adjacency list
In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node...
. Because each entry in the adjacency matrix requires only one bit, it can be represented in a very compact way, occupying only
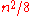 bytes of contiguous space, where
bytes of contiguous space, where  is the number of vertices. Besides avoiding wasted space, this compactness encourages locality of reference
is the number of vertices. Besides avoiding wasted space, this compactness encourages locality of referenceLocality of reference
In computer science, locality of reference, also known as the principle of locality, is the phenomenon of the same value or related storage locations being frequently accessed. There are two basic types of reference locality. Temporal locality refers to the reuse of specific data and/or resources...
.
In contrast, for a sparse graph adjacency lists win out, because they use no space to represent edges that are not present. Using a naïve array implementation on a 32-bit computer, an adjacency list for an undirected graph requires about
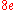 bytes of storage, where
bytes of storage, where  is the number of edges.
is the number of edges.Noting that a simple graph can have at most
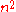 edges, allowing loops, we can let
edges, allowing loops, we can let 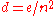 denote the density of the graph. Then,
denote the density of the graph. Then,  , or the adjacency list representation occupies more space precisely when
, or the adjacency list representation occupies more space precisely when  . Thus a graph must be sparse indeed to justify an adjacency list representation.
. Thus a graph must be sparse indeed to justify an adjacency list representation.Besides the space tradeoff, the different data structures also facilitate different operations. Finding all vertices adjacent to a given vertex in an adjacency list is as simple as reading the list. With an adjacency matrix, an entire row must instead be scanned, which takes O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n) time. Whether there is an edge between two given vertices can be determined at once with an adjacency matrix, while requiring time proportional to the minimum degree of the two vertices with the adjacency list.
External links
- Fluffschack — an educational Java web start game demonstrating the relationship between adjacency matrices and graphs.

