Adelic algebraic group
Encyclopedia
In abstract algebra
, an adelic algebraic group is a topological group
defined by an algebraic group
G over a number field K, and the adele ring
A = A(K) of K. It consists of the points of G having values in A; the definition of the appropriate topology
is straightforward only in case G is a linear algebraic group
. In the case of G an abelian variety
it presents a technical obstacle, though it is known that the concept is potentially useful in connection with Tamagawa numbers. Adelic algebraic groups are widely used in number theory
, particularly for the theory of automorphic representations, and the arithmetic of quadratic forms.
In case G is a linear algebraic group, it is an affine algebraic variety in affine N-space. The topology on the adelic algebraic group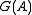
is taken to be the subspace topology
in AN, the Cartesian product
of N copies of the adele ring.
An important example, the idele group I(K), is the case of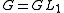
. Here the set of ideles (correctly, idèles) consists of the invertible adeles; but the topology on the idele group is not their topology as a subset of the adeles. Instead, considering that 
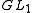lies in two-dimensional affine space
as the 'hyperbola
' defined parametrically by
the topology correctly assigned to the idele group is that induced by inclusion in A2; composing with a projection, we see that the ideles carry a finer topology than the subspace topology from A.
Inside AN, the product KN lies as a discrete subgroup. This means that G(K) is a discrete subgroup of G(A), also. In the case of the idele group, the quotient group
is the idele class group. It is closely related to (though larger than) the ideal class group
. The idele class group is not itself compact; the ideles must first be replaced by the ideles of norm 1, and then the image of those in the idele class group is a compact group
; the proof of this is essentially equivalent to the finiteness of the class number.
The study of the Galois cohomology
of idele class groups is a central matter in class field theory
. Characters of the idele class group, now usually called Hecke character
s, give rise to the most basic class of L-function
s.
For more general G, the Tamagawa number is defined (or indirectly computed) as the measure of
Tsuneo Tamagawa
's observation was that, starting from an invariant differential form
ω on G, defined over K, the measure involved was well-defined
: while ω could be replaced by cω with c a non-zero element of K, the product formula for valuation
s in K is reflected by the independence from c of the measure of the quotient, for the product measure constructed from ω on each effective factor. The computation of Tamagawa numbers for semisimple groups contains important parts of classical quadratic form
theory.
. This was to formulate class field theory
for infinite extensions in terms of topological groups. Shortly afterwards the adèles (additive idèles) were used by André Weil
, to formulate a proof of the Riemann-Roch theorem. 'Adèle' being a French girls' name, this joke was not acceptable to some, who preferred the term répartitions. The general construction of adelic algebraic groups in the 1950s followed the algebraic group theory founded by Armand Borel
and Harish-Chandra
, and at this point the terminology became fixed.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an adelic algebraic group is a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
defined by an algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G over a number field K, and the adele ring
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
A = A(K) of K. It consists of the points of G having values in A; the definition of the appropriate topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is straightforward only in case G is a linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
. In the case of G an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
it presents a technical obstacle, though it is known that the concept is potentially useful in connection with Tamagawa numbers. Adelic algebraic groups are widely used in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, particularly for the theory of automorphic representations, and the arithmetic of quadratic forms.
In case G is a linear algebraic group, it is an affine algebraic variety in affine N-space. The topology on the adelic algebraic group
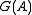is taken to be the subspace topologySubspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
in AN, the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of N copies of the adele ring.
An important example, the idele group I(K), is the case of
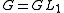. Here the set of ideles (correctly, idèles) consists of the invertible adeles; but the topology on the idele group is not their topology as a subset of the adeles. Instead, considering that 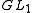lies in two-dimensional affine spaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
as the 'hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
' defined parametrically by
- {(t, t−1)},
the topology correctly assigned to the idele group is that induced by inclusion in A2; composing with a projection, we see that the ideles carry a finer topology than the subspace topology from A.
Inside AN, the product KN lies as a discrete subgroup. This means that G(K) is a discrete subgroup of G(A), also. In the case of the idele group, the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
- I(K)/K×
is the idele class group. It is closely related to (though larger than) the ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
. The idele class group is not itself compact; the ideles must first be replaced by the ideles of norm 1, and then the image of those in the idele class group is a compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
; the proof of this is essentially equivalent to the finiteness of the class number.
The study of the Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
of idele class groups is a central matter in class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
. Characters of the idele class group, now usually called Hecke character
Hecke character
In number theory, a Hecke character is a generalisation of a Dirichlet character, introduced by Erich Hecke to construct a class ofL-functions larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations analogous to...
s, give rise to the most basic class of L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s.
For more general G, the Tamagawa number is defined (or indirectly computed) as the measure of
- G(A)/G(K).
Tsuneo Tamagawa
Tsuneo Tamagawa
Tsuneo Tamagawa is a mathematician. He works on the arithmetic of classical groups.He has been on the Yale University faculty since 1963, and became emeritus in 1996.-References:*...
's observation was that, starting from an invariant differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
ω on G, defined over K, the measure involved was well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
: while ω could be replaced by cω with c a non-zero element of K, the product formula for valuation
Valuation
-Economics:*Valuation , the determination of the economic value of an asset or liability**Real estate appraisal, sometimes called property valuation , the appraisal of land or buildings...
s in K is reflected by the independence from c of the measure of the quotient, for the product measure constructed from ω on each effective factor. The computation of Tamagawa numbers for semisimple groups contains important parts of classical quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
theory.
History of the terminology
Historically the idèles were introduced first in the mid-1930s, by Claude ChevalleyClaude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
. This was to formulate class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
for infinite extensions in terms of topological groups. Shortly afterwards the adèles (additive idèles) were used by André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, to formulate a proof of the Riemann-Roch theorem. 'Adèle' being a French girls' name, this joke was not acceptable to some, who preferred the term répartitions. The general construction of adelic algebraic groups in the 1950s followed the algebraic group theory founded by Armand Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
and Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, and at this point the terminology became fixed.