3D projection
Encyclopedia
3D projection is any method of mapping three-dimensional points to a two-dimensional plane. As most current methods for displaying graphical data are based on planar two-dimensional media, the use of this type of projection is widespread, especially in computer graphics, engineering and drafting
.
Orthographic projection
s are a small set of transforms often used to show profile, detail or precise measurements of a three dimensional object. Common names for orthographic projections include plane, cross-section, bird's-eye, and elevation.
If the normal of the viewing plane (the camera direction) is parallel to one of the primary axes (which is the x, y, or z axis), the mathematical transformation is as follows;
To project the 3D point ,
,  ,
,  onto the 2D point
onto the 2D point  ,
,  using an orthographic projection parallel to the y axis (profile view), the following equations can be used:
using an orthographic projection parallel to the y axis (profile view), the following equations can be used:

where the vector s is an arbitrary scale factor, and c is an arbitrary offset. These constants are optional, and can be used to properly align the viewport. Using matrix multiplication
, the equations become: .
.
While orthographically projected images represent the three dimensional nature of the object projected, they do not represent the object as it would be recorded photographically or perceived by a viewer observing it directly. In particular, parallel lengths at all points in an orthographically projected image are of the same scale regardless of whether they are far away or near to the virtual viewer. As a result, lengths near to the viewer are not foreshortened as they would be in a perspective projection.
. While orthographic projection ignores this effect to allow accurate measurements, perspective definition shows distant objects as smaller to provide additional realism.
The perspective projection requires greater definition. A conceptual aid to understanding the mechanics of this projection involves treating the 2D projection as being viewed through a camera viewfinder. The camera's position, orientation, and field of view
control the behavior of the projection transformation. The following variables are defined to describe this transformation:
Which results in:
When and
and  the 3D vector
the 3D vector  is projected to the 2D vector
is projected to the 2D vector  .
.
Otherwise, to compute we first define a vector
we first define a vector  as the position of point A with respect to a coordinate system
as the position of point A with respect to a coordinate system
defined by the camera, with origin in C and rotated by with respect to the initial coordinate system. This is achieved by subtracting
with respect to the initial coordinate system. This is achieved by subtracting
 from
from  and then applying a rotation by
and then applying a rotation by  to the result. This transformation is often called a , and can be expressed as follows, expressing the rotation in terms of rotations about the x, y, and z axes (these calculations assume that the axes are ordered as a left-handed system of axes):
to the result. This transformation is often called a , and can be expressed as follows, expressing the rotation in terms of rotations about the x, y, and z axes (these calculations assume that the axes are ordered as a left-handed system of axes):

This representation corresponds to rotating by three Euler angles
(more properly, Tait–Bryan angles), using the xyz convention, which can be interpreted either as "rotate about the extrinsic axes (axes of the scene) in the order z, y, x (reading right-to-left)" or "rotate about the intrinsic axes (axes of the camera) in the order x, y, z) (reading left-to-right)". Note that if the camera is not rotated ( ), then the matrices drop out (as identities), and this reduces to simply a shift:
), then the matrices drop out (as identities), and this reduces to simply a shift: 
Alternatively, without using matrices, (note that the signs of angles are inconsistent with matrix form):
This transformed point can then be projected onto the 2D plane using the formula (here, x/y is used as the projection plane; literature also may use x/z):
Or, in matrix form using homogeneous coordinates
, the system
in conjunction with an argument using similar triangles, leads to division by the homogeneous coordinate, giving
The distance of the viewer from the display surface, , directly relates to the field of view, where
, directly relates to the field of view, where  is the viewed angle. (Note: This assumes that you map the points (-1,-1) and (1,1) to the corners of your viewing surface)
is the viewed angle. (Note: This assumes that you map the points (-1,-1) and (1,1) to the corners of your viewing surface)
The above equations can also be rewritten as:
In which is the display size,
is the display size,  is the recording surface size (CCD
is the recording surface size (CCD
or film
), is the distance from the recording surface to the entrance pupil
is the distance from the recording surface to the entrance pupil
(camera center), and is the distance, from the 3D point being projected, to the entrance pupil.
is the distance, from the 3D point being projected, to the entrance pupil.
Subsequent clipping and scaling operations may be necessary to map the 2D plane onto any particular display media.
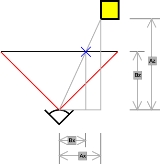
To determine which screen x-coordinate corresponds to a point at multiply the point coordinates by:
multiply the point coordinates by:
where is the screen x coordinate
is the screen x coordinate is the model x coordinate
is the model x coordinate is the focal length
is the focal length
—the axial distance from the camera center to the image plane
 is the subject distance.
is the subject distance.
Because the camera is in 3D, the same works for the screen y-coordinate, substituting y for x in the above diagram and equation.
Technical drawing
Technical drawing, also known as drafting or draughting, is the act and discipline of composing plans that visually communicate how something functions or has to be constructed.Drafting is the language of industry....
.
Orthographic projection
When the human eye looks at a scene, objects in the distance appear smaller than objects close by. Orthographic projection ignores this effect to allow the creation of to-scale drawings for construction and engineering.Orthographic projection
Orthographic projection
Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...
s are a small set of transforms often used to show profile, detail or precise measurements of a three dimensional object. Common names for orthographic projections include plane, cross-section, bird's-eye, and elevation.
If the normal of the viewing plane (the camera direction) is parallel to one of the primary axes (which is the x, y, or z axis), the mathematical transformation is as follows;
To project the 3D point
 ,
,  ,
,  onto the 2D point
onto the 2D point  ,
,  using an orthographic projection parallel to the y axis (profile view), the following equations can be used:
using an orthographic projection parallel to the y axis (profile view), the following equations can be used:

where the vector s is an arbitrary scale factor, and c is an arbitrary offset. These constants are optional, and can be used to properly align the viewport. Using matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, the equations become:
 .
.While orthographically projected images represent the three dimensional nature of the object projected, they do not represent the object as it would be recorded photographically or perceived by a viewer observing it directly. In particular, parallel lengths at all points in an orthographically projected image are of the same scale regardless of whether they are far away or near to the virtual viewer. As a result, lengths near to the viewer are not foreshortened as they would be in a perspective projection.
Perspective projection
When the human eye looks at a scene, objects in the distance appear smaller than objects close by - this is known as perspectivePerspective (graphical)
Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...
. While orthographic projection ignores this effect to allow accurate measurements, perspective definition shows distant objects as smaller to provide additional realism.
The perspective projection requires greater definition. A conceptual aid to understanding the mechanics of this projection involves treating the 2D projection as being viewed through a camera viewfinder. The camera's position, orientation, and field of view
Field of view
The field of view is the extent of the observable world that is seen at any given moment....
control the behavior of the projection transformation. The following variables are defined to describe this transformation:
-
 - the 3D position of a point A that is to be projected.
- the 3D position of a point A that is to be projected. -
 - the 3D position of a point C representing the camera.
- the 3D position of a point C representing the camera. -
 - The orientationOrientation (geometry)In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
- The orientationOrientation (geometry)In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
of the camera (represented, for instance, by Tait–Bryan angles). -
 - the viewer's position relative to the display surface.
- the viewer's position relative to the display surface.
Which results in:
-
 - the 2D projection of
- the 2D projection of  .
.
When
 and
and  the 3D vector
the 3D vector  is projected to the 2D vector
is projected to the 2D vector  .
.Otherwise, to compute
 we first define a vector
we first define a vector  as the position of point A with respect to a coordinate system
as the position of point A with respect to a coordinate systemCoordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
defined by the camera, with origin in C and rotated by
 with respect to the initial coordinate system. This is achieved by subtracting
with respect to the initial coordinate system. This is achieved by subtractingMatrix addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum....
 from
from  and then applying a rotation by
and then applying a rotation by  to the result. This transformation is often called a , and can be expressed as follows, expressing the rotation in terms of rotations about the x, y, and z axes (these calculations assume that the axes are ordered as a left-handed system of axes):
to the result. This transformation is often called a , and can be expressed as follows, expressing the rotation in terms of rotations about the x, y, and z axes (these calculations assume that the axes are ordered as a left-handed system of axes):
This representation corresponds to rotating by three Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
(more properly, Tait–Bryan angles), using the xyz convention, which can be interpreted either as "rotate about the extrinsic axes (axes of the scene) in the order z, y, x (reading right-to-left)" or "rotate about the intrinsic axes (axes of the camera) in the order x, y, z) (reading left-to-right)". Note that if the camera is not rotated (
 ), then the matrices drop out (as identities), and this reduces to simply a shift:
), then the matrices drop out (as identities), and this reduces to simply a shift: 
Alternatively, without using matrices, (note that the signs of angles are inconsistent with matrix form):

This transformed point can then be projected onto the 2D plane using the formula (here, x/y is used as the projection plane; literature also may use x/z):

Or, in matrix form using homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
, the system

in conjunction with an argument using similar triangles, leads to division by the homogeneous coordinate, giving

The distance of the viewer from the display surface,
 , directly relates to the field of view, where
, directly relates to the field of view, where  is the viewed angle. (Note: This assumes that you map the points (-1,-1) and (1,1) to the corners of your viewing surface)
is the viewed angle. (Note: This assumes that you map the points (-1,-1) and (1,1) to the corners of your viewing surface)The above equations can also be rewritten as:

In which
 is the display size,
is the display size,  is the recording surface size (CCD
is the recording surface size (CCDCharge-coupled device
A charge-coupled device is a device for the movement of electrical charge, usually from within the device to an area where the charge can be manipulated, for example conversion into a digital value. This is achieved by "shifting" the signals between stages within the device one at a time...
or film
Film
A film, also called a movie or motion picture, is a series of still or moving images. It is produced by recording photographic images with cameras, or by creating images using animation techniques or visual effects...
),
 is the distance from the recording surface to the entrance pupil
is the distance from the recording surface to the entrance pupilEntrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front of the lens system. The corresponding image of the aperture as seen through the back of the lens system is called the exit pupil...
(camera center), and
 is the distance, from the 3D point being projected, to the entrance pupil.
is the distance, from the 3D point being projected, to the entrance pupil.Subsequent clipping and scaling operations may be necessary to map the 2D plane onto any particular display media.
Diagram

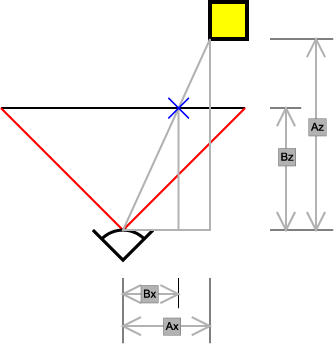
To determine which screen x-coordinate corresponds to a point at
 multiply the point coordinates by:
multiply the point coordinates by:
where
 is the screen x coordinate
is the screen x coordinate is the model x coordinate
is the model x coordinate is the focal length
is the focal lengthFocal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
—the axial distance from the camera center to the image plane
Image plane
In 3D computer graphics, the image plane is that plane in the world which is identified with the plane of the monitor. If one makes the analogy of taking a photograph to rendering a 3D image, the surface of the film is the image plane. In this case, the viewing transformation is a projection that...
 is the subject distance.
is the subject distance.Because the camera is in 3D, the same works for the screen y-coordinate, substituting y for x in the above diagram and equation.
See also
- Computer graphicsComputer graphicsComputer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
- 3D computer graphics3D computer graphics3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
- Graphics card
- Transform and lighting
- Texture mappingTexture mappingTexture mapping is a method for adding detail, surface texture , or color to a computer-generated graphic or 3D model. Its application to 3D graphics was pioneered by Dr Edwin Catmull in his Ph.D. thesis of 1974.-Texture mapping:...
- Perspective (graphical)Perspective (graphical)Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...
- Camera matrixCamera matrixIn computer vision a camera matrix or projection matrix is a 3 \times 4 matrix which describes the mapping of a pinhole camera from 3D points in the world to 2D points in an image....
- HomographyHomographyHomography is a concept in the mathematical science of geometry.A homography is an invertible transformation from a projective space to itself that maps straight lines to straight lines...
- Homogeneous coordinatesHomogeneous coordinatesIn mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...

