Woodin cardinal
Encyclopedia
In set theory
, a Woodin cardinal (named for W. Hugh Woodin
) is a cardinal number
λ such that for all functions
there exists a cardinal κ < λ with
and an elementary embedding
from V into a transitive inner model
M with critical point
κ and
An equivalent definition is this: λ is Woodin if and only if
λ is strongly inaccessible
and for all
there exists a 
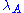< λ which is 
-
-strong.
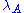being 
-
-strong means that for all ordinals
α < λ, there exist a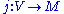
which is an elementary embedding with critical point
, 
, 
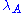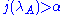and 
. (See also strong cardinal
.)
A Woodin cardinal is preceded by a stationary set
of measurable cardinal
s, and thus it is a Mahlo cardinal
. However, the first Woodin cardinal is not even weakly compact
.
. By a result of Martin
and Steel
, existence of infinitely many Woodin cardinals implies projective determinacy, which in turn implies that every projective set is measurable, has the Baire property (differs from an open set by a meager set
, that is, a set which is a countable union of nowhere dense sets), and the perfect set property
(is either countable or contains a perfect subset).
The consistency of the existence of Woodin cardinals can be proved using determinacy hypotheses. Working in ZF
+AD
+DC
one can prove that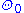
is Woodin in the class of hereditarily ordinal-definable sets. 
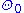is the first ordinal onto which the continuum cannot be mapped by an ordinal-definable surjection (see Θ (set theory)).
Shelah
proved that if the existence of a Woodin cardinal is consistent then it is consistent that the nonstationary ideal on ω1 is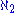
-saturated.
Woodin also proved the equiconsistency of the existence of infinitely many Woodin cardinals and the existence of an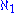
-dense ideal over 
.
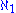κ is called hyper-Woodin if there exists a normal measure
U on κ such that for every set S, the set
is in U.
λ is <κ-S-strong if and only if for each δ < κ there is a transitive class N and an elementary embedding
with
.
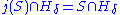The name alludes to the classical result that a cardinal is Woodin if and only if for every set S, the set
is a stationary set
The measure U will contain the set of all Shelah cardinals below κ.
κ is called weakly hyper-Woodin if for every set S there exists a normal measure
U on κ such that the set {λ < κ | λ is <κ-S-strong} is in U. λ is <κ-S-strong if and only if for each δ < κ there is a transitive class N and an elementary
embedding j : V → N with λ = crit(j), j(λ) >= δ, and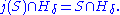
The name alludes to the classic result that a cardinal is Woodin if for every set S, the set {λ < κ | λ is <κ-S-strong
} is stationary.
The difference between hyper-Woodin cardinals and weakly hyper-Woodin cardinals is that the choice of U does not depend on the choice of the set S for hyper-Woodin cardinals.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a Woodin cardinal (named for W. Hugh Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
) is a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
λ such that for all functions
- f : λ → λ
there exists a cardinal κ < λ with
- {f(β)|β < κ} ⊆ κ
and an elementary embedding
- j : V → M
from V into a transitive inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
M with critical point
Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
κ and
- Vj(f)(κ) ⊆ M.
An equivalent definition is this: λ is Woodin if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
λ is strongly inaccessible
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
and for all
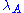there exists a < λ which is --strong.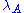 being --strong means that for all ordinalsOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
α < λ, there exist a
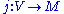which is an elementary embedding with critical pointCritical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
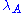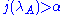, , and . (See also strong cardinalStrong cardinal
In set theory, a strong cardinal is a type of large cardinal. It is a weakening of the notion of a supercompact cardinal.- Formal definition :...
.)
A Woodin cardinal is preceded by a stationary set
Stationary set
In mathematics, particularly in set theory and model theory, there are at least three notions of stationary set:-Classical notion:If \kappa \, is a cardinal of uncountable cofinality, S \subseteq \kappa \,, and S \, intersects every club set in \kappa \,, then S \, is called a stationary set....
of measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
s, and thus it is a Mahlo cardinal
Mahlo cardinal
In mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
. However, the first Woodin cardinal is not even weakly compact
Weakly compact cardinal
In mathematics, a weakly compact cardinal is a certain kind of cardinal number introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory....
.
Consequences
Woodin cardinals are important in descriptive set theoryDescriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
. By a result of Martin
Donald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
and Steel
John R. Steel
John Robert Steel is a set theorist at University of California, Berkeley . He has made many contributions to the theory of inner models and determinacy. With Donald A. Martin, he proved projective determinacy, assuming the existence of sufficient large cardinals. He earned his Ph.D...
, existence of infinitely many Woodin cardinals implies projective determinacy, which in turn implies that every projective set is measurable, has the Baire property (differs from an open set by a meager set
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
, that is, a set which is a countable union of nowhere dense sets), and the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
(is either countable or contains a perfect subset).
The consistency of the existence of Woodin cardinals can be proved using determinacy hypotheses. Working in ZF
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
+AD
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
+DC
Axiom of dependent choice
In mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
one can prove that
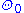is Woodin in the class of hereditarily ordinal-definable sets. 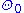is the first ordinal onto which the continuum cannot be mapped by an ordinal-definable surjection (see Θ (set theory)).Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
proved that if the existence of a Woodin cardinal is consistent then it is consistent that the nonstationary ideal on ω1 is
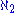-saturated.Woodin also proved the equiconsistency of the existence of infinitely many Woodin cardinals and the existence of an
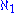-dense ideal over 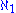.Hyper-Woodin cardinals
A cardinalCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ is called hyper-Woodin if there exists a normal measure
Normal measure
In set theory, a normal measure is a measure on a measurable cardinal κ such that the equivalence class of the identity function on κ maps to κ itself in the ultrapower construction...
U on κ such that for every set S, the set
- {λ < κ | λ is <κ-S-strongStrong cardinalIn set theory, a strong cardinal is a type of large cardinal. It is a weakening of the notion of a supercompact cardinal.- Formal definition :...
}
is in U.
λ is <κ-S-strong if and only if for each δ < κ there is a transitive class N and an elementary embedding
- j : V → N
with
- λ = crit(j),
- j(λ)≥ δ, and
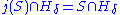.The name alludes to the classical result that a cardinal is Woodin if and only if for every set S, the set
- {λ < κ | λ is <κ-S-strongStrong cardinalIn set theory, a strong cardinal is a type of large cardinal. It is a weakening of the notion of a supercompact cardinal.- Formal definition :...
}
is a stationary set
Stationary set
In mathematics, particularly in set theory and model theory, there are at least three notions of stationary set:-Classical notion:If \kappa \, is a cardinal of uncountable cofinality, S \subseteq \kappa \,, and S \, intersects every club set in \kappa \,, then S \, is called a stationary set....
The measure U will contain the set of all Shelah cardinals below κ.
Weakly hyper-Woodin cardinals
A cardinalCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ is called weakly hyper-Woodin if for every set S there exists a normal measure
Normal measure
In set theory, a normal measure is a measure on a measurable cardinal κ such that the equivalence class of the identity function on κ maps to κ itself in the ultrapower construction...
U on κ such that the set {λ < κ | λ is <κ-S-strong} is in U. λ is <κ-S-strong if and only if for each δ < κ there is a transitive class N and an elementary
embedding j : V → N with λ = crit(j), j(λ) >= δ, and
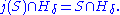
The name alludes to the classic result that a cardinal is Woodin if for every set S, the set {λ < κ | λ is <κ-S-strong
Strong cardinal
In set theory, a strong cardinal is a type of large cardinal. It is a weakening of the notion of a supercompact cardinal.- Formal definition :...
} is stationary.
The difference between hyper-Woodin cardinals and weakly hyper-Woodin cardinals is that the choice of U does not depend on the choice of the set S for hyper-Woodin cardinals.
Further reading
- For proofs of the two results listed in consequences see Handbook of Set Theory (Eds. Foreman, Kanamori, Magidor) (to appear). Drafts of some chapters are available.
- Ernest Schimmerling, Woodin cardinals, Shelah cardinals and the Mitchell-Steel core model, Proceedings of the American Mathematical Society 130/11, pp. 3385–3391, 2002, online