
Inaccessible cardinal
Encyclopedia
In set theory
, an uncountable
regular cardinal number
is called weakly inaccessible if it is a weak limit cardinal
, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable (in which case is strongly inaccessible). Weakly inaccessible cardinals were introduced by , and strongly inaccessible ones by and .
is strongly inaccessible). Weakly inaccessible cardinals were introduced by , and strongly inaccessible ones by and .
The term "inaccessible cardinal" is ambiguous. Until about 1950 it meant "weakly inaccessible cardinal", but since then it usually means "strongly inaccessible cardinal".
Every strongly inaccessible cardinal is also weakly inaccessible, as every strong limit cardinal is also a weak limit cardinal. If the generalized continuum hypothesis holds, then a cardinal is strongly inaccessible if and only if it is weakly inaccessible.
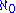 (aleph-null
(aleph-null
) is a regular strong limit cardinal. Assuming the axiom of choice, every other infinite cardinal number is either regular or a (weak) limit. However, only a rather large cardinal number can be both and thus weakly inaccessible.
An ordinal
is a weakly inaccessible cardinal if and only if it is a regular ordinal and it is a limit of regular ordinals. (Zero, one, and are regular ordinals, but not limits of regular ordinals.) A cardinal which is weakly inaccessible and also a strong limit cardinal is strongly inaccessible.
are regular ordinals, but not limits of regular ordinals.) A cardinal which is weakly inaccessible and also a strong limit cardinal is strongly inaccessible.
The assumption of the existence of a strongly inaccessible cardinal is sometimes applied in the form of the assumption that one can work inside a Grothendieck universe
, the two ideas being intimately connected.
of ZFC whenever κ is strongly inaccessible. And ZF implies that the Gödel universe Lκ is a model of ZFC whenever κ is weakly inaccessible. Thus ZF together with "there exists a weakly inaccessible cardinal" implies that ZFC is consistent. Therefore, inaccessible cardinals are a type of large cardinal.
If V is a standard model of ZFC and κ is an inaccessible in V, then: Vκ is one of the intended models of Zermelo–Fraenkel set theory
; and Def (Vκ) is one of the intended models of Von Neumann–Bernays–Gödel set theory
; and Vκ+1 is one of the intended models of Morse–Kelley set theory
. Here Def (X) is the Δ0 definable subsets of X (see constructible universe
). However, κ does not need to be inaccessible, or even a cardinal number, in order for Vκ to be a standard model of ZF (see below).
Suppose V is a model of ZFC. Either V contains no strong inaccessible or, taking κ to be the smallest strong inaccessible in V, Vκ is a standard model of ZFC which contains no strong inaccessibles. Thus, the consistency of ZFC implies consistency of ZFC+"there are no strong inaccessibles". Similarly, either V contains no weak inaccessible or, taking κ to be the smallest ordinal which is weakly inaccessible relative to any standard sub-model of V, then Lκ is a standard model of ZFC which contains no weak inaccessibles. So consistency of ZFC implies consistency of ZFC+"there are no weak inaccessibles". This shows that ZFC cannot prove the existence of an inaccessible cardinal, so ZFC is consistent with the non-existence of any inaccessible cardinals.
The issue whether ZFC is consistent with the existence of an inaccessible cardinal is more subtle. The proof sketched in the previous paragraph that the consistency of ZFC + "there is an inaccessible cardinal" implies the consistency of ZFC + "there is not an inaccessible cardinal" can be formalized in ZFC. However, no proof that the consistency of ZFC implies the consistency of ZFC + "there is an inaccessible cardinal" can be formalized in ZFC. This follows from Gödel's second incompleteness theorem, which shows that if ZFC + "there is an inaccessible cardinal" is consistent, then it cannot prove its own consistency. Because ZFC + "there is an inaccessible cardinal" does prove the consistency of ZFC, if ZFC proved that its own consistency implies the consistency of ZFC + "there is an inaccessible cardinal" then this latter theory would be able to prove its own consistency, which is impossible.
There are arguments for the existence of inaccessible cardinals that cannot be formalized in ZFC. One such argument, presented by , is that the class of all ordinals of a particular model M of set theory would itself be an inaccessible cardinal if there was a larger model of set theory extending M.
: every set is contained in a Grothendieck universe
. The axioms of ZFC along with the universe axiom (or equivalently the inaccessible cardinal axiom) are denoted ZFCU (which could be confused with ZFC with urelements). This axiomatic system is useful to prove for example that every category
has an appropriate Yoneda embedding.
This is a relatively weak large cardinal axiom since it amounts to saying that ∞ is 1-inaccessible in the language of the next section, where ∞ denotes the least ordinal not in V, i.e. the class of all ordinals in your model.
The α-inaccessible cardinals can be equivalently described as fixed points of functions which count the lower inaccessibles. For example, denote by ψ0(λ) the λth inaccessible cardinal, then the fixed points of ψ0 are the 1-inaccessible cardinals. Then letting ψβ(λ) be the λth β-inaccessible cardinal, the fixed points of ψβ are the (β+1)-inaccessible cardinals (the values ψβ+1(λ)). If α is a limit ordinal, an α-inaccessible is a fixed point of every ψβ for β < α (the value ψα(λ) is the λth such cardinal). This process of taking fixed points of functions generating successively larger cardinals is commonly encountered in the study of large cardinal numbers.
The term hyper-inaccessible is ambiguous. Some authors use it to mean 1-inaccessible, though this use is rare. Most authors use it to mean that κ is κ-inaccessible. (It can never be κ+1-inaccessible.)
For any ordinal α, a cardinal κ is α-hyper-inaccessible if and only if κ is hyper-inaccessible and for every ordinal β < α, the set of β-hyper-inaccessibles less than κ is unbounded in κ.
Hyper-hyper-inaccessible cardinals and so on can be defined in a similar way.
Using "weakly inaccessible" instead of "inaccessible", similar definitions can be made for "weakly α-inaccessible", "weakly hyper-inaccessible", and "weakly α-hyper-inaccessible".
Mahlo cardinal
s are inaccessible, hyper-inaccessible, hyper-hyper-inaccessible, ... and so on.
property: for all subsets U ⊂ Vκ, there exists α < κ such that is an elementary substructure
is an elementary substructure
of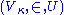 . (In fact, the set of such α is closed unbounded
. (In fact, the set of such α is closed unbounded
in κ.) Equivalently, κ is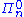 -indescribable
-indescribable
for all n ≥ 0.
It is provable in ZF that ∞ satisfies a somewhat weaker reflection property, where the substructure (Vα, ∈, U ∩ Vα) is only required to be 'elementary' with respect to a finite set of formulas. Ultimately, the reason for this weakening is that whereas the model-theoretic satisfaction relation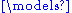 can be defined, truth itself cannot, due to Tarski's theorem.
can be defined, truth itself cannot, due to Tarski's theorem.
Secondly, under ZFC it can be shown that κ is inaccessible if and only if (Vκ, ∈) is a model of second order ZFC.
In this case, by the reflection property above, there exists α < κ such that (Vα, ∈) is a standard model of (first order) ZFC. Hence, the existence of an inaccessible cardinal is a stronger hypothesis than the existence of a standard model of ZFC.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
regular cardinal number
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
is called weakly inaccessible if it is a weak limit cardinal
Limit cardinal
In mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ by repeated successor operations...
, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable (in which case
 is strongly inaccessible). Weakly inaccessible cardinals were introduced by , and strongly inaccessible ones by and .
is strongly inaccessible). Weakly inaccessible cardinals were introduced by , and strongly inaccessible ones by and .The term "inaccessible cardinal" is ambiguous. Until about 1950 it meant "weakly inaccessible cardinal", but since then it usually means "strongly inaccessible cardinal".
Every strongly inaccessible cardinal is also weakly inaccessible, as every strong limit cardinal is also a weak limit cardinal. If the generalized continuum hypothesis holds, then a cardinal is strongly inaccessible if and only if it is weakly inaccessible.
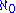 (aleph-null
(aleph-nullAleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
) is a regular strong limit cardinal. Assuming the axiom of choice, every other infinite cardinal number is either regular or a (weak) limit. However, only a rather large cardinal number can be both and thus weakly inaccessible.
An ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
is a weakly inaccessible cardinal if and only if it is a regular ordinal and it is a limit of regular ordinals. (Zero, one, and
 are regular ordinals, but not limits of regular ordinals.) A cardinal which is weakly inaccessible and also a strong limit cardinal is strongly inaccessible.
are regular ordinals, but not limits of regular ordinals.) A cardinal which is weakly inaccessible and also a strong limit cardinal is strongly inaccessible.The assumption of the existence of a strongly inaccessible cardinal is sometimes applied in the form of the assumption that one can work inside a Grothendieck universe
Grothendieck universe
In mathematics, a Grothendieck universe is a set U with the following properties:# If x is an element of U and if y is an element of x, then y is also an element of U...
, the two ideas being intimately connected.
Models and consistency
ZFC implies that the Vκ is a modelModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of ZFC whenever κ is strongly inaccessible. And ZF implies that the Gödel universe Lκ is a model of ZFC whenever κ is weakly inaccessible. Thus ZF together with "there exists a weakly inaccessible cardinal" implies that ZFC is consistent. Therefore, inaccessible cardinals are a type of large cardinal.
If V is a standard model of ZFC and κ is an inaccessible in V, then: Vκ is one of the intended models of Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
; and Def (Vκ) is one of the intended models of Von Neumann–Bernays–Gödel set theory
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
; and Vκ+1 is one of the intended models of Morse–Kelley set theory
Morse–Kelley set theory
In the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
. Here Def (X) is the Δ0 definable subsets of X (see constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
). However, κ does not need to be inaccessible, or even a cardinal number, in order for Vκ to be a standard model of ZF (see below).
Suppose V is a model of ZFC. Either V contains no strong inaccessible or, taking κ to be the smallest strong inaccessible in V, Vκ is a standard model of ZFC which contains no strong inaccessibles. Thus, the consistency of ZFC implies consistency of ZFC+"there are no strong inaccessibles". Similarly, either V contains no weak inaccessible or, taking κ to be the smallest ordinal which is weakly inaccessible relative to any standard sub-model of V, then Lκ is a standard model of ZFC which contains no weak inaccessibles. So consistency of ZFC implies consistency of ZFC+"there are no weak inaccessibles". This shows that ZFC cannot prove the existence of an inaccessible cardinal, so ZFC is consistent with the non-existence of any inaccessible cardinals.
The issue whether ZFC is consistent with the existence of an inaccessible cardinal is more subtle. The proof sketched in the previous paragraph that the consistency of ZFC + "there is an inaccessible cardinal" implies the consistency of ZFC + "there is not an inaccessible cardinal" can be formalized in ZFC. However, no proof that the consistency of ZFC implies the consistency of ZFC + "there is an inaccessible cardinal" can be formalized in ZFC. This follows from Gödel's second incompleteness theorem, which shows that if ZFC + "there is an inaccessible cardinal" is consistent, then it cannot prove its own consistency. Because ZFC + "there is an inaccessible cardinal" does prove the consistency of ZFC, if ZFC proved that its own consistency implies the consistency of ZFC + "there is an inaccessible cardinal" then this latter theory would be able to prove its own consistency, which is impossible.
There are arguments for the existence of inaccessible cardinals that cannot be formalized in ZFC. One such argument, presented by , is that the class of all ordinals of a particular model M of set theory would itself be an inaccessible cardinal if there was a larger model of set theory extending M.
Existence of a proper class of inaccessibles
There are many important axioms in set theory which assert the existence of a proper class of cardinals which satisfy a predicate of interest. In the case of inaccessibility, the corresponding axiom is the assertion that for every cardinal μ, there is an inaccessible cardinal κ which is strictly larger, μ < κ. Thus this axiom guarantees the existence of an infinite tower of inaccessible cardinals (and may occasionally be referred to as the inaccessible cardinal axiom). As is the case for the existence of any inaccessible cardinal, the inaccessible cardinal axiom is unprovable from the axioms of ZFC. Assuming ZFC, the inaccessible cardinal axiom is equivalent to the universe axiom of Grothendieck and VerdierJean-Louis Verdier
Jean-Louis Verdier was a French mathematician who worked, under the guidance of Alexander Grothendieck, on derived categories and Verdier duality...
: every set is contained in a Grothendieck universe
Grothendieck universe
In mathematics, a Grothendieck universe is a set U with the following properties:# If x is an element of U and if y is an element of x, then y is also an element of U...
. The axioms of ZFC along with the universe axiom (or equivalently the inaccessible cardinal axiom) are denoted ZFCU (which could be confused with ZFC with urelements). This axiomatic system is useful to prove for example that every category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
has an appropriate Yoneda embedding.
This is a relatively weak large cardinal axiom since it amounts to saying that ∞ is 1-inaccessible in the language of the next section, where ∞ denotes the least ordinal not in V, i.e. the class of all ordinals in your model.
α-inaccessible cardinals and hyper-inaccessible cardinals
A cardinal κ is α-inaccessible, for α any ordinal, if and only if κ is inaccessible and for every ordinal β < α, the set of β-inaccessibles less than κ is unbounded in κ (and thus of cardinality κ, since κ is regular).The α-inaccessible cardinals can be equivalently described as fixed points of functions which count the lower inaccessibles. For example, denote by ψ0(λ) the λth inaccessible cardinal, then the fixed points of ψ0 are the 1-inaccessible cardinals. Then letting ψβ(λ) be the λth β-inaccessible cardinal, the fixed points of ψβ are the (β+1)-inaccessible cardinals (the values ψβ+1(λ)). If α is a limit ordinal, an α-inaccessible is a fixed point of every ψβ for β < α (the value ψα(λ) is the λth such cardinal). This process of taking fixed points of functions generating successively larger cardinals is commonly encountered in the study of large cardinal numbers.
The term hyper-inaccessible is ambiguous. Some authors use it to mean 1-inaccessible, though this use is rare. Most authors use it to mean that κ is κ-inaccessible. (It can never be κ+1-inaccessible.)
For any ordinal α, a cardinal κ is α-hyper-inaccessible if and only if κ is hyper-inaccessible and for every ordinal β < α, the set of β-hyper-inaccessibles less than κ is unbounded in κ.
Hyper-hyper-inaccessible cardinals and so on can be defined in a similar way.
Using "weakly inaccessible" instead of "inaccessible", similar definitions can be made for "weakly α-inaccessible", "weakly hyper-inaccessible", and "weakly α-hyper-inaccessible".
Mahlo cardinal
Mahlo cardinal
In mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
s are inaccessible, hyper-inaccessible, hyper-hyper-inaccessible, ... and so on.
Two model-theoretic characterisations of inaccessibility
Firstly, a cardinal κ is inaccessible if and only if κ has the following reflectionReflection principle
In set theory, a branch of mathematics, a reflection principle says that it is possible to find sets that resemble the class of all sets. There are several different forms of the reflection principle depending on exactly what is meant by "resemble"...
property: for all subsets U ⊂ Vκ, there exists α < κ such that
 is an elementary substructure
is an elementary substructureElementary substructure
In model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
of
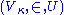 . (In fact, the set of such α is closed unbounded
. (In fact, the set of such α is closed unboundedClub set
In mathematics, particularly in mathematical logic and set theory, a club set is a subset of a limit ordinal which is closed under the order topology, and is unbounded relative to the limit ordinal...
in κ.) Equivalently, κ is
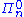 -indescribable
-indescribableTotally indescribable cardinal
In mathematics, a Q-indescribable cardinal is a certain kind of large cardinal number that is hard to describe in some language Q. There are many different types of indescribable cardinals corresponding to different choices of languages Q...
for all n ≥ 0.
It is provable in ZF that ∞ satisfies a somewhat weaker reflection property, where the substructure (Vα, ∈, U ∩ Vα) is only required to be 'elementary' with respect to a finite set of formulas. Ultimately, the reason for this weakening is that whereas the model-theoretic satisfaction relation
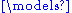 can be defined, truth itself cannot, due to Tarski's theorem.
can be defined, truth itself cannot, due to Tarski's theorem.Secondly, under ZFC it can be shown that κ is inaccessible if and only if (Vκ, ∈) is a model of second order ZFC.
In this case, by the reflection property above, there exists α < κ such that (Vα, ∈) is a standard model of (first order) ZFC. Hence, the existence of an inaccessible cardinal is a stronger hypothesis than the existence of a standard model of ZFC.
See also
- Mahlo cardinalMahlo cardinalIn mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
- Club setClub setIn mathematics, particularly in mathematical logic and set theory, a club set is a subset of a limit ordinal which is closed under the order topology, and is unbounded relative to the limit ordinal...
- Inner modelInner modelIn mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
- Von Neumann universeVon Neumann universeIn set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
- Constructible universeConstructible universeIn mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...

