
Model category
Encyclopedia
In mathematics
, particularly in homotopy theory, a model category is a category
with distinguished classes of morphism
s ('arrows') called 'weak equivalence
s', 'fibration
s' and 'cofibration
s'. These abstract from a conventional homotopy category, of topological space
s or of chain complex
es (derived category
theory). This concept was introduced by .
s.
Another model category is the category of chain complex
es of R-modules for a commutative ring R. Homotopy theory in this context is homological algebra
. Homology can then be viewed as a type of homotopy, allowing generalizations of homology to other objects, such as groups and R-algebras, one of the first major applications of the theory. Because of the above example regarding homology, the study of closed model categories is sometimes thought of as homotopical algebra
.
The definition has been separated to that of a model structure on a category and then further categorical conditions on that category, the necessity of which may seem unmotivated at first but becomes important later. The following definition follows that given by Hovey.
A model structure on a category C consists of three distinguished classes of morphisms (equivalently subcategories): weak equivalence
s, fibration
s, and cofibration
s, and two functorial factorizations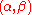 and
and 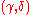 subject to the following axioms. Note that a fibration that is also a weak equivalence is called an acyclic (or trivial) fibration and a cofibration that is also a weak equivalence is called an acyclic (or trivial) cofibration (or sometimes called an anodyne morphism). (Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".)
subject to the following axioms. Note that a fibration that is also a weak equivalence is called an acyclic (or trivial) fibration and a cofibration that is also a weak equivalence is called an acyclic (or trivial) cofibration (or sometimes called an anodyne morphism). (Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".)
Axioms:
A model category is a category that has a model structure and all (small) limits and colimits, i.e. a complete and cocomplete category
with a model structure.
, Top, admits a standard model category structure with the usual (Serre) fibrations
and cofibration
s and with weak equivalences as weak homotopy equivalences. This structure is not unique; in general there can be many model category structures on a given category. For the category of topological spaces, another such structure is given by Hurewicz fibrations and cofibrations.
The category of (nonnegatively graded) chain complexes of R-modules carries at least two model structures, which both feature prominently in homological algebra:
or
This explains why Ext-groups of R-modules can be computed by either resolving the source projectively or the target injectively. These are cofibrant or fibrant replacements in the respective model structures.
The category of arbitrary chain-complexes of R-modules has a model structure that is defined by
Other examples of categories admitting model structures include the category of all small categories, the category of simplicial set
s or simplicial presheaves on any small Grothendieck site, the category of topological spectra, and the categories of simplicial spectra or presheaves of simplicial spectra on a small Grothendieck site.
Simplicial objects in a category are a frequent source of model categories; for instance, simplicial commutative rings or simplicial R-modules admit natural model structures. This follows because there is an adjunction between simplicial sets and simplicial commutative rings (given by the forgetful and free functors), and in nice cases one can lift model structures under an adjunction.
Denis-Charles Cisinski has developed a general theory of model structures on presheaf categories (generalizing simplicial sets, which are presheaves on the simplex category).
by cocompleteness, since these objects are the limit and colimit, respectively, of the empty diagram. Given an object X in the model category, if the unique map from the initial object to X is a cofibration, then X is said to be cofibrant. Analogously, if the unique map from X to the terminal object is a fibration then X is said to be fibrant.
If Z and X are objects of a model category such that Z is cofibrant and there is a weak equivalence from Z to X then Z is said to be a cofibrant replacement for X. Similarly, if Z is fibrant and there is a weak equivalence from X to Z then Z is said to be a fibrant
replacement for X. In general, not all objects are fibrant or cofibrant, though this is sometimes the case. For example, all objects are cofibrant in the standard model category of simplicial sets and all objects are fibrant for the standard model category structure given above for topological spaces.
Left homotopy is defined with respect to cylinder objects and right homotopy is defined with respect to path objects. These notions coincide when the domain is cofibrant and the codomain is fibrant. In that case, homotopy defines an equivalence relation on the hom sets in the model category giving rise to homotopy classes.
with respect to the class of weak equivalences. This suggests that the information regarding homotopy is contained in the class of weak equivalences whereas the classes of fibrations and cofibrations are useful in making constructions within the category. For example, the homotopy category for the model category structure on topological spaces given above is the category of CW-complexes. This is also true for the model category of simplicial sets. Simplicial sets have nice combinatorial properties and are often used as models for topological spaces because of the equivalence of the homotopy categories.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in homotopy theory, a model category is a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
with distinguished classes of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s ('arrows') called 'weak equivalence
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
s', 'fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s' and 'cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
s'. These abstract from a conventional homotopy category, of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s or of chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es (derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
theory). This concept was introduced by .
Motivation
Model categories can provide a natural setting for homotopy theory: the category of topological spaces is a model category, with the homotopy corresponding to the usual theory. Similarly, objects that are thought of as spaces often admit a model category structure, such as the category of simplicial setSimplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s.
Another model category is the category of chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es of R-modules for a commutative ring R. Homotopy theory in this context is homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
. Homology can then be viewed as a type of homotopy, allowing generalizations of homology to other objects, such as groups and R-algebras, one of the first major applications of the theory. Because of the above example regarding homology, the study of closed model categories is sometimes thought of as homotopical algebra
Homotopical algebra
In mathematics, homotopical algebra is a collection of concepts comprising the nonabelian aspects of homological algebra as well as possibly the abelian aspects as special cases...
.
Formal definition
The definition given initially by Quillen was that of a closed model category, the assumptions of which seemed strong at the time, motivating others to weaken some of the assumptions to define a model category. In practice the distinction has not proven significant and most recent authors work with closed model categories and simply drop the adjective 'closed'.The definition has been separated to that of a model structure on a category and then further categorical conditions on that category, the necessity of which may seem unmotivated at first but becomes important later. The following definition follows that given by Hovey.
A model structure on a category C consists of three distinguished classes of morphisms (equivalently subcategories): weak equivalence
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
s, fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s, and cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
s, and two functorial factorizations
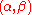 and
and 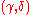 subject to the following axioms. Note that a fibration that is also a weak equivalence is called an acyclic (or trivial) fibration and a cofibration that is also a weak equivalence is called an acyclic (or trivial) cofibration (or sometimes called an anodyne morphism). (Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".)
subject to the following axioms. Note that a fibration that is also a weak equivalence is called an acyclic (or trivial) fibration and a cofibration that is also a weak equivalence is called an acyclic (or trivial) cofibration (or sometimes called an anodyne morphism). (Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".)Axioms:
- Retracts: if g is a morphism belonging to one of the distinguished classes, and f is a retract of g (as objects in the arrow category
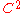 , where 2 is the 2-element ordered set), then f belongs to the same distinguished class. Explicitly, the requirement that f is a retract of g means that there exist i, j, r, and s, such that the following diagram commutes:
, where 2 is the 2-element ordered set), then f belongs to the same distinguished class. Explicitly, the requirement that f is a retract of g means that there exist i, j, r, and s, such that the following diagram commutes:
- 2 of 3: if f and g are maps in C such that f, g, and gf are defined and any two of these are weak equivalences then so is the third.
- Lifting: acyclic cofibrations have the left lifting property with respect to fibrations and cofibrations have the left lifting property with respect to acyclic fibrations. Explicitly, if the outer square of the following diagram commutes, where i is a cofibration and p is a fibration, and i or p is acyclic, then there exists h completing the diagram.
- Factorization:
- every morphism f in C, can be written as
 for a fibration p and an acyclic cofibration i;
for a fibration p and an acyclic cofibration i; - every morphism f in C, can be written as
 for an acyclic fibration p and a cofibration i.
for an acyclic fibration p and a cofibration i.
- every morphism f in C, can be written as
A model category is a category that has a model structure and all (small) limits and colimits, i.e. a complete and cocomplete category
Complete category
In mathematics, a complete category is a category in which all small limits exist. That is, a category C is complete if every diagram F : J → C where J is small has a limit in C. Dually, a cocomplete category is one in which all small colimits exist...
with a model structure.
Examples
The category of topological spacesCategory of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, Top, admits a standard model category structure with the usual (Serre) fibrations
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
and cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
s and with weak equivalences as weak homotopy equivalences. This structure is not unique; in general there can be many model category structures on a given category. For the category of topological spaces, another such structure is given by Hurewicz fibrations and cofibrations.
The category of (nonnegatively graded) chain complexes of R-modules carries at least two model structures, which both feature prominently in homological algebra:
- weak equivalences are maps that induce isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s in homology; - cofibrations are maps that are monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s in each degree with projective cokernelCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
; and - fibrations are maps that are epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s in each nonzero degree
or
- weak equivalences are maps that induce isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s in homology; - fibrations are maps that are epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s in each degree with injective kernelKernel (category theory)In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
; and - cofibrations are maps that are monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s in each nonzero degree.
This explains why Ext-groups of R-modules can be computed by either resolving the source projectively or the target injectively. These are cofibrant or fibrant replacements in the respective model structures.
The category of arbitrary chain-complexes of R-modules has a model structure that is defined by
- weak equivalences are chain homotopy equivalences of chain-complexes;
- cofibrations are monomorphisms that are split as morphisms of underlying R-modules; and
- fibrations are epimorphisms that are split as morphisms of underlying R-modules.
Other examples of categories admitting model structures include the category of all small categories, the category of simplicial set
Simplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s or simplicial presheaves on any small Grothendieck site, the category of topological spectra, and the categories of simplicial spectra or presheaves of simplicial spectra on a small Grothendieck site.
Simplicial objects in a category are a frequent source of model categories; for instance, simplicial commutative rings or simplicial R-modules admit natural model structures. This follows because there is an adjunction between simplicial sets and simplicial commutative rings (given by the forgetful and free functors), and in nice cases one can lift model structures under an adjunction.
Denis-Charles Cisinski has developed a general theory of model structures on presheaf categories (generalizing simplicial sets, which are presheaves on the simplex category).
Some constructions
Every closed model category has a terminal object by completeness and an initial objectInitial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
by cocompleteness, since these objects are the limit and colimit, respectively, of the empty diagram. Given an object X in the model category, if the unique map from the initial object to X is a cofibration, then X is said to be cofibrant. Analogously, if the unique map from X to the terminal object is a fibration then X is said to be fibrant.
If Z and X are objects of a model category such that Z is cofibrant and there is a weak equivalence from Z to X then Z is said to be a cofibrant replacement for X. Similarly, if Z is fibrant and there is a weak equivalence from X to Z then Z is said to be a fibrant
replacement for X. In general, not all objects are fibrant or cofibrant, though this is sometimes the case. For example, all objects are cofibrant in the standard model category of simplicial sets and all objects are fibrant for the standard model category structure given above for topological spaces.
Left homotopy is defined with respect to cylinder objects and right homotopy is defined with respect to path objects. These notions coincide when the domain is cofibrant and the codomain is fibrant. In that case, homotopy defines an equivalence relation on the hom sets in the model category giving rise to homotopy classes.
Characterizations of fibrations and cofibrations by lifting properties
Cofibrations can be characterized as the maps which have the left lifting property with respect to acyclic fibrations, and acyclic cofibrations are characterized as the maps which have the left lifting property with respect to fibrations. Similarly, fibrations can be characterized as the maps which have the right lifting property with respect to acyclic cofibrations, and acyclic fibrations are characterized as the maps which have the rightlifting property with respect to cofibrations.Homotopy and the homotopy category
Given a model category, one can then define an associated homotopy category by localizingLocalization of a category
In mathematics, localization of a category consists of adding to a category inverse morphisms for some collection of morphisms, constraining them to become isomorphisms. This is formally similar to the process of localization of a ring; it in general makes objects isomorphic that were not so before...
with respect to the class of weak equivalences. This suggests that the information regarding homotopy is contained in the class of weak equivalences whereas the classes of fibrations and cofibrations are useful in making constructions within the category. For example, the homotopy category for the model category structure on topological spaces given above is the category of CW-complexes. This is also true for the model category of simplicial sets. Simplicial sets have nice combinatorial properties and are often used as models for topological spaces because of the equivalence of the homotopy categories.
External links
- Model category in ncatlab
- Model category in Joyal's catlab

