
Weyl's lemma (Laplace equation)
Encyclopedia
In mathematics
, Weyl's lemma is a result that provides a "very weak" form of the Laplace equation. It is named after the German
mathematician
Hermann Weyl
.
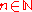 and let
and let  be an open subset
be an open subset
of . Let
. Let  denote the usual Laplace operator
denote the usual Laplace operator
. Suppose that is locally integrable (i.e.,
is locally integrable (i.e.,  ) and that
) and that
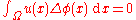
 (Eq. 1)
(Eq. 1)
for every smooth
function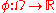 with compact support in
with compact support in  . Then, possibly after redefinition on a set of measure zero,
. Then, possibly after redefinition on a set of measure zero,  is smooth and has
is smooth and has  in
in 
the function with an appropriate mollifier
with an appropriate mollifier
, and then showing that the resulting function satisfies the mean value property, which is equivalent to being harmonic. The nature of the mollifer chosen means that, except on a set of measure zero, the function is equal to its own mollifier.
is equal to its own mollifier.
s. For example, one way to see why the lemma holds is to note that elliptic operators do not shrink singular support and that has no singular support.
has no singular support.
 with
with  in some domain of interest,
in some domain of interest,  . The usual weak formulation is to seek weakly differentiable functions
. The usual weak formulation is to seek weakly differentiable functions  such that
such that

 (Eq. 2)
(Eq. 2)
for every in the Sobolev space
in the Sobolev space
 . A solution of (Eq. 2) will also satisfy (Eq. 1) above, and the converse holds if, in addition,
. A solution of (Eq. 2) will also satisfy (Eq. 1) above, and the converse holds if, in addition, 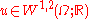 . Consequently, one can view (Eq. 1) as a "very weak" form of the Laplace equation, and a solution of (Eq. 1) as a "very weak" solution of
. Consequently, one can view (Eq. 1) as a "very weak" form of the Laplace equation, and a solution of (Eq. 1) as a "very weak" solution of  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Weyl's lemma is a result that provides a "very weak" form of the Laplace equation. It is named after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
.
Statement of the lemma
Let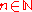 and let
and let  be an open subset
be an open subsetOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of
 . Let
. Let  denote the usual Laplace operator
denote the usual Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
. Suppose that
 is locally integrable (i.e.,
is locally integrable (i.e.,  ) and that
) and that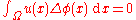
 (Eq. 1)
(Eq. 1)for every smooth
Smooth
Smooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...
function
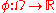 with compact support in
with compact support in  . Then, possibly after redefinition on a set of measure zero,
. Then, possibly after redefinition on a set of measure zero,  is smooth and has
is smooth and has  in
in 
Heuristic of the proof
Weyl's lemma can be proved by convolvingConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
the function
 with an appropriate mollifier
with an appropriate mollifierMollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
, and then showing that the resulting function satisfies the mean value property, which is equivalent to being harmonic. The nature of the mollifer chosen means that, except on a set of measure zero, the function
 is equal to its own mollifier.
is equal to its own mollifier.Generalization
Weyl's lemma follows from more general results concerning regularity properties of elliptic operatorElliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
s. For example, one way to see why the lemma holds is to note that elliptic operators do not shrink singular support and that
 has no singular support.
has no singular support."Weak" and "very weak" forms of the Laplace equation
The strong formulation of the Laplace equation is to seek functions with
with  in some domain of interest,
in some domain of interest,  . The usual weak formulation is to seek weakly differentiable functions
. The usual weak formulation is to seek weakly differentiable functions  such that
such that
 (Eq. 2)
(Eq. 2)for every
 in the Sobolev space
in the Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
 . A solution of (Eq. 2) will also satisfy (Eq. 1) above, and the converse holds if, in addition,
. A solution of (Eq. 2) will also satisfy (Eq. 1) above, and the converse holds if, in addition, 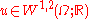 . Consequently, one can view (Eq. 1) as a "very weak" form of the Laplace equation, and a solution of (Eq. 1) as a "very weak" solution of
. Consequently, one can view (Eq. 1) as a "very weak" form of the Laplace equation, and a solution of (Eq. 1) as a "very weak" solution of  .
.

