Waring's problem
Encyclopedia
In number theory
, Waring's problem, proposed in 1770 by Edward Waring
, asks whether for every natural number
k there exists an associated positive integer
s such that every natural number is the sum of at most s kth powers of natural numbers (for example, every number is the sum of at most 4 squares, or 9 cubes, or 19 fourth powers, etc.). The affirmative answer, known as the Hilbert–Waring theorem, was provided by Hilbert
in 1909. Waring's problem has its own Mathematics Subject Classification
, 11P05, "Waring's problem and variants."
Lagrange's four-square theorem
of 1770 states that every natural number is the sum of at most four squares; since three squares are not enough, this theorem establishes g(2) = 4. Lagrange's four-square theorem was conjectured in Bachet
's 1621 edition of Diophantus
; Fermat
claimed to have a proof, but did not publish it.
Over the years various bounds were established, using increasingly sophisticated and complex proof techniques. For example, Liouville
showed that g(4) is at most 53. Hardy
and Littlewood
showed that all sufficiently large numbers are the sum of at most 19 fourth powers.
That g(3) = 9 was established from 1909 to 1912 by Wieferich
and A. J. Kempner, g(4) = 19 in 1986 by R. Balasubramanian
, F. Dress, and J.-M. Deshouillers, g(5) = 37 in 1964 by Chen Jingrun
, and g(6) = 73 in 1940 by Pillai
.
Let [x] and {x} denote the integral and fractional part
of x respectively. Since 2k[(3/2)k]-1<3k only 2k and 1k can be used to represent this number and the most economical representation requires [(3/2)k]-1 2ks and 2k-1 1ks it follows that g(k) is at least as large as 2k + [(3/2)k] − 2. J. A. Euler, the son of Leonard Euler, conjectured about 1772 that, in fact, g(k) = 2k + [(3/2)k] − 2. Later work by Dickson
, Pillai, Rubugunday, Niven
and many others have proved that
No values of k are known for which 2k{(3/2)k} + [(3/2)k] > 2k, Mahler
has proved there can only be a finite number of such k and Kubina and Wunderlich have shown that any such k must satisfy k > 471,600,000. Thus it is conjectured that this never happens, i.e. that g(k) = 2k + [(3/2)k] − 2 for each positive integer k.
The first few values of g(k) are 1, 4, 9, 19
, 37
, 73
, 143
, 279, 548, 1079, 2132, 4223, 8384, 16673, 33203, 66190, 132055 ... .
and Littlewood
, more fundamental than g(k) turned out to be G(k), which is defined to be the least positive integer s such that every sufficiently large integer (i.e. every integer greater than some constant) can be represented as a sum of at most s kth powers of positive integers. Since squares are congruent to 0, 1, or 4 (mod 8), no integer congruent to 7 (mod 8) can be represented as a sum of three squares, implying that G(2) ≥ 4. Since G(k) ≤ g(k) for all k, this shows that G(2) = 4. Davenport
showed that G(4) = 16 in 1939, by demonstrating that any sufficiently large number congruent to 1 through 14 mod 16 could be written as a sum of 14 fourth powers (Vaughan in 1985 and 1989 reduced the 14 successively to 13 and 12). The exact value of G(k) is unknown for any other k, but there exist bounds.
The number G(k) is greater than or equal to
In the absence of congruence restrictions, a density argument suggests that G(k) should equal k + 1.
13792 is the largest number to require seventeen fourth powers (Deshouillers, Hennecart and Landreau showed in 2000 that every number between 13793 and 10245 required at most sixteen, and Kawada, Wooley and Deshouillers extended Davenport's 1939 result to show that every number above 10220 required no more than sixteen). Sixteen fourth powers are always needed to write a number of the form 31·16n.
617597724 is the last number less than 1.3 which requires ten fifth powers, and 51033617 the last number less than 1.3 which requires eleven.
The upper bounds on the right with k=5,...,20 are due to Vaughan and Wooley
[1993], [1994], [1995], [2000] (see Vaughan and Wooley [2002]).
Using his improved Hardy-Littlewood method, I. M. Vinogradov
published numerous refinements leading to
in 1947 and, ultimately,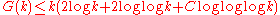
for an unspecified constant C and sufficiently large k in 1959.
Applying his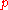 -adic form of the Hardy-Littlewood-Ramanujan-Vinogradov method to estimating trigonometric sums, in which the summation is taken over numbers with small prime divisors, Anatolii Alexeevitch Karatsuba
-adic form of the Hardy-Littlewood-Ramanujan-Vinogradov method to estimating trigonometric sums, in which the summation is taken over numbers with small prime divisors, Anatolii Alexeevitch Karatsuba
obtained (1985) a new estimate of the Hardy
function (for
(for  ):
):
Further in his investigation of the Waring problem Karatsuba obtained the following two-dimensional generalization of that problem:
Consider the system of equations
where are given positive integers with the same order or growth,
are given positive integers with the same order or growth,  , and
, and  are unknowns, which are also positive integers. This system has solutions, if
are unknowns, which are also positive integers. This system has solutions, if  , and if
, and if  ,
,
then there exist such , that the system has no solutions.
, that the system has no solutions.
Further minor refinements were obtained by Vaughan [1989].
Wooley then established that for some constant C (See for a proof.)
(See for a proof.)
Vaughan and Wooley have written a comprehensive survey article [2002].
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Waring's problem, proposed in 1770 by Edward Waring
Edward Waring
Edward Waring was an English mathematician who was born in Old Heath , Shropshire, England and died in Pontesbury, Shropshire, England. He entered Magdalene College, Cambridge as a sizar and became Senior wrangler in 1757. He was elected a Fellow of Magdalene and in 1760 Lucasian Professor of...
, asks whether for every natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
k there exists an associated positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s such that every natural number is the sum of at most s kth powers of natural numbers (for example, every number is the sum of at most 4 squares, or 9 cubes, or 19 fourth powers, etc.). The affirmative answer, known as the Hilbert–Waring theorem, was provided by Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
in 1909. Waring's problem has its own Mathematics Subject Classification
Mathematics Subject Classification
The Mathematics Subject Classification is an alphanumerical classification scheme collaboratively produced by staff of and based on the coverage of the two major mathematical reviewing databases, Mathematical Reviews and Zentralblatt MATH...
, 11P05, "Waring's problem and variants."
The number g(k)
For every k, we denote by g(k) the minimum number s of kth powers needed to represent all integers. Note we have g(1) = 1. Some simple computations show that 7 requires 4 squares, 23 requires 9 cubes, and 79 requires 19 fourth-powers; these examples show that g(2) ≥ 4, g(3) ≥ 9, and g(4) ≥ 19. Waring conjectured that these values were in fact the best possible.Lagrange's four-square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
of 1770 states that every natural number is the sum of at most four squares; since three squares are not enough, this theorem establishes g(2) = 4. Lagrange's four-square theorem was conjectured in Bachet
Claude Gaspard Bachet de Méziriac
Claude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse.Bachet was a pupil of the Jesuit mathematician Jacques de Billy at the Jesuit College in Rheims...
's 1621 edition of Diophantus
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
; Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
claimed to have a proof, but did not publish it.
Over the years various bounds were established, using increasingly sophisticated and complex proof techniques. For example, Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
showed that g(4) is at most 53. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Littlewood
John Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
showed that all sufficiently large numbers are the sum of at most 19 fourth powers.
That g(3) = 9 was established from 1909 to 1912 by Wieferich
Arthur Wieferich
Arthur Josef Alwin Wieferich was a German mathematician and teacher, remembered for his work on number theory....
and A. J. Kempner, g(4) = 19 in 1986 by R. Balasubramanian
Ramachandran Balasubramanian
Ramachandran Balasubramanian is an Indian mathematician and is currently the Director of the Institute of Mathematical Sciences in Chennai, India...
, F. Dress, and J.-M. Deshouillers, g(5) = 37 in 1964 by Chen Jingrun
Chen Jingrun
Chen Jingrun was a Chinese mathematician who made significant contributions to number theory.- Personal life :Chen was the third son in a large family from Fuzhou, Fujian, China. His father was a postal worker. Chen Jingrun graduated from the Mathematics Department of Xiamen University in 1953...
, and g(6) = 73 in 1940 by Pillai
Subbayya Sivasankaranarayana Pillai
Subbayya Sivasankaranarayana Pillai was an Indian mathematician, well known for his work in number theory. He was from Tamil Nadu....
.
Let [x] and {x} denote the integral and fractional part
Fractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
of x respectively. Since 2k[(3/2)k]-1<3k only 2k and 1k can be used to represent this number and the most economical representation requires [(3/2)k]-1 2ks and 2k-1 1ks it follows that g(k) is at least as large as 2k + [(3/2)k] − 2. J. A. Euler, the son of Leonard Euler, conjectured about 1772 that, in fact, g(k) = 2k + [(3/2)k] − 2. Later work by Dickson
Leonard Eugene Dickson
Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory.-Life:Dickson considered himself a Texan by...
, Pillai, Rubugunday, Niven
Ivan M. Niven
Ivan Morton Niven was a Canadian-American mathematician, specializing in number theory. He was born in Vancouver. He did his undergraduate studies at the University of British Columbia and was awarded his doctorate in 1938 from the University of Chicago. He was a member of the University of Oregon...
and many others have proved that
- g(k) = 2k + [(3/2)k] − 2 if 2k{(3/2)k} + [(3/2)k] ≤ 2k
- g(k) = 2k + [(3/2)k] + [(4/3)k] − 2 if 2k{(3/2)k} + [(3/2)k] > 2k and [(4/3)k][(3/2)k] + [(4/3)k] + [(3/2)k] = 2k
- g(k) = 2k + [(3/2)k] + [(4/3)k] − 3 if 2k{(3/2)k} + [(3/2)k] > 2k and [(4/3)k][(3/2)k] + [(4/3)k] + [(3/2)k] > 2k.
No values of k are known for which 2k{(3/2)k} + [(3/2)k] > 2k, Mahler
Kurt Mahler
Kurt Mahler was a mathematician and Fellow of the Royal Society.He was a student at the universities in Frankfurt and Göttingen, graduating with a Ph.D...
has proved there can only be a finite number of such k and Kubina and Wunderlich have shown that any such k must satisfy k > 471,600,000. Thus it is conjectured that this never happens, i.e. that g(k) = 2k + [(3/2)k] − 2 for each positive integer k.
The first few values of g(k) are 1, 4, 9, 19
19 (number)
19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90...
, 37
37 (number)
37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form...
, 73
73 (number)
73 is the natural number following 72 and preceding 74. In English, it is the smallest integer with twelve letters in its spelled out name.- In mathematics :...
, 143
143 (number)
143 is the natural number following 142 and preceding 144.-In mathematics:143 is the sum of three consecutive primes , as well as the sum of seven consecutive primes...
, 279, 548, 1079, 2132, 4223, 8384, 16673, 33203, 66190, 132055 ... .
The number G(k)
From the work of HardyG. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Littlewood
John Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
, more fundamental than g(k) turned out to be G(k), which is defined to be the least positive integer s such that every sufficiently large integer (i.e. every integer greater than some constant) can be represented as a sum of at most s kth powers of positive integers. Since squares are congruent to 0, 1, or 4 (mod 8), no integer congruent to 7 (mod 8) can be represented as a sum of three squares, implying that G(2) ≥ 4. Since G(k) ≤ g(k) for all k, this shows that G(2) = 4. Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
showed that G(4) = 16 in 1939, by demonstrating that any sufficiently large number congruent to 1 through 14 mod 16 could be written as a sum of 14 fourth powers (Vaughan in 1985 and 1989 reduced the 14 successively to 13 and 12). The exact value of G(k) is unknown for any other k, but there exist bounds.
Lower bounds for G(k)
| Bounds |
|---|
| 4 ≤ G(2) ≤ 4 |
| 4 ≤ G(3) ≤ 7 |
| 16 ≤ G(4) ≤ 16 |
| 6 ≤ G(5) ≤ 17 |
| 9 ≤ G(6) ≤ 24 |
| 8 ≤ G(7) ≤ 33 |
| 32 ≤ G(8) ≤ 42 |
| 13 ≤ G(9) ≤ 50 |
| 12 ≤ G(10) ≤ 59 |
| 12 ≤ G(11) ≤ 67 |
| 16 ≤ G(12) ≤ 76 |
| 14 ≤ G(13) ≤ 84 |
| 15 ≤ G(14) ≤ 92 |
| 16 ≤ G(15) ≤ 100 |
| 64 ≤ G(16) ≤ 109 |
| 18 ≤ G(17) ≤ 117 |
| 27 ≤ G(18) ≤ 125 |
| 20 ≤ G(19) ≤ 134 |
| 25 ≤ G(20) ≤ 142 |
The number G(k) is greater than or equal to
- 2r + 2 if k = 2r with r ≥ 2, or k = 3×2r;
- pr + 1 if p is a prime greater than 2 and k = pr(p − 1);/2 if p is a prime greater than 2 and k = pr(p − 1)/2;
- k + 1 for all integers k greater than 1.
In the absence of congruence restrictions, a density argument suggests that G(k) should equal k + 1.
Upper bounds for G(k)
G(3) is at least four (since cubes are congruent to 0, 1 or −1 mod 9); for numbers less than 1.3, 1290740 is the last to require six cubes, and the number of numbers between N and 2N requiring five cubes drops off with increasing N at sufficient speed to have people believe G(3)=4; the largest number now known not to be a sum of four cubes is 7373170279850, and the authors give reasonable arguments there that this may be the largest possible.13792 is the largest number to require seventeen fourth powers (Deshouillers, Hennecart and Landreau showed in 2000 that every number between 13793 and 10245 required at most sixteen, and Kawada, Wooley and Deshouillers extended Davenport's 1939 result to show that every number above 10220 required no more than sixteen). Sixteen fourth powers are always needed to write a number of the form 31·16n.
617597724 is the last number less than 1.3 which requires ten fifth powers, and 51033617 the last number less than 1.3 which requires eleven.
The upper bounds on the right with k=5,...,20 are due to Vaughan and Wooley
Trevor Wooley
Trevor D. Wooley FRS is a British mathematician and currently Professor of Mathematics at the University of Bristol. His fields of interest include analytic number theory, Diophantine equations and Diophantine problems, harmonic analysis,...
[1993], [1994], [1995], [2000] (see Vaughan and Wooley [2002]).
Using his improved Hardy-Littlewood method, I. M. Vinogradov
Ivan Matveyevich Vinogradov
Ivan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
published numerous refinements leading to

in 1947 and, ultimately,
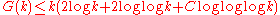
for an unspecified constant C and sufficiently large k in 1959.
Applying his
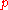 -adic form of the Hardy-Littlewood-Ramanujan-Vinogradov method to estimating trigonometric sums, in which the summation is taken over numbers with small prime divisors, Anatolii Alexeevitch Karatsuba
-adic form of the Hardy-Littlewood-Ramanujan-Vinogradov method to estimating trigonometric sums, in which the summation is taken over numbers with small prime divisors, Anatolii Alexeevitch KaratsubaAnatolii Alexeevitch Karatsuba
Anatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
obtained (1985) a new estimate of the Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
function
 (for
(for  ):
):Further in his investigation of the Waring problem Karatsuba obtained the following two-dimensional generalization of that problem:
Consider the system of equations
-
 ,
,  ,
,
where
 are given positive integers with the same order or growth,
are given positive integers with the same order or growth,  , and
, and  are unknowns, which are also positive integers. This system has solutions, if
are unknowns, which are also positive integers. This system has solutions, if  , and if
, and if  ,
,then there exist such
 , that the system has no solutions.
, that the system has no solutions.Further minor refinements were obtained by Vaughan [1989].
Wooley then established that for some constant C
 (See for a proof.)
(See for a proof.)Vaughan and Wooley have written a comprehensive survey article [2002].
Further reading
- W. J. Ellison: Waring's problem. American Mathematical Monthly, volume 78 (1971), pp. 10–36. Survey, contains the precise formula for g(k), a simplified version of Hilbert's proof and a wealth of references. Has an elementary proof of the existence of G(k) using Schnirelmann densitySchnirelmann densityIn additive number theory, the Schnirelmann density of a sequence of numbers is a way to measure how "dense" the sequence is. It is named after Russian mathematician L.G...
. Has proofs of Lagrange's theorem, the polygonal number theorem, Hilbert's proof of Waring's conjecture and the Hardy-Littlewood proof of the asymptotic formula for the number of ways to represent N as the sum of s kth powers. - Hans RademacherHans RademacherHans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...
and Otto ToeplitzOtto ToeplitzOtto Toeplitz was a German Jewish mathematician working in functional analysis.- Life and work :...
, The Enjoyment of Mathematics (1933) (ISBN 0-691-02351-4). Has a proof of the Lagrange theorem, accessible to high school students.