
Verdier duality
Encyclopedia
In mathematics, Verdier duality is a generalization of the Poincaré duality
of manifold
s to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality
for schemes due to Grothendieck. It plays a role in the theory of perverse sheaves.
The exclamation mark
is often pronounced "shriek
" (slang for exclamation mark), and the maps called "f shriek" or "f lower shriek" and "f upper shriek" – see also shriek map
.
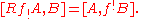
If X is a finite covering space of Y then f! takes sheaves to sheaves and is the same as f∗. If X is a closed subspace of Y then f! again takes sheaves to sheaves, but in general its image on sheaves cannot be represented by a single sheaf, but only by a complex of sheaves on the derived category.
Local Verdier duality states that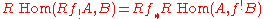
in the right derived category
of sheaves of F modules over X.
Taking homology of both sides gives global Verdier duality.
The dualizing complex DX on X is defined to be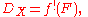
where f is the map from X to a point.
If X is a finite dimensional locally compact space, and Db(X) the bounded derived category
of sheaves of abelian groups over X, then the Verdier dual is a contravariant functor
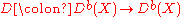
defined by

It has the following properties:
Here Rf∗ denotes the higher direct image, at the derived category level.
In the special case when Y is a point and X is compact this says (roughly) that the cohomologies of dual complexes are dual.
is a special case of Verdier duality; this can be seen as follows.
In the derived category, cohomology can be interpreted as chain homotopy classes of maps
where F[−k] is the complex with the constant sheaf
F concentrated in degree k, and [—, —] denote the chain homotopy classes of maps. The Verdier dual allows us to interpret homology in the derived category as well:
The left hand side is by definition the dual of the cohomology with compact support, so this equation says that homology is dual to cohomology with compact support.
It also follows that for an oriented manifold
M, the Verdier dual is given by
Ordinary Poincaré duality of a manifold can then be interpreted as the perfect pairing
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
of manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality
Coherent duality
In mathematics, coherent duality is any of a number of generalisations of Serre duality, applying to coherent sheaves, in algebraic geometry and complex manifold theory, as well as some aspects of commutative algebra that are part of the 'local' theory....
for schemes due to Grothendieck. It plays a role in the theory of perverse sheaves.
Notation
- F is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. - The dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of a locally compact spaceLocally compact spaceIn topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
is the smallest integer n such that Hcn+1(X,S) = 0 for all abelian sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
S (or infinity if no such integer n exists). - X and Y are finite dimensional locally compact spaces, and f is a continuous map from X to Y.
- [A,B] is the set of morphisms between elements A and B of the derived categoryDerived categoryIn mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of sheaves on a space. - f∗ and f∗ are the usual directDirect image functorIn mathematics, in the field of sheaf theory and especially in algebraic geometry, the direct image functor generalizes the notion of a section of a sheaf to the relative case.-Definition:...
and inverse image functorInverse image functorIn mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
s between sheaves induced by f. The functor f∗ is the left adjoint of f∗. - f! is the direct image with compact supportDirect image with compact supportIn mathematics, in the theory of sheaves the direct image with compact support is an image functor for sheaves.-Definition:Let f: X → Y be a continuous mapping of topological spaces, and Sh the category of sheaves of abelian groups on a topological space...
and Rf! is the exceptional inverse image functorExceptional inverse image functorIn mathematics, more specifically sheaf theory, a branch of topology and algebraic geometry, the exceptional inverse image functor is the fourth and most sophisticated in a series of image functors for sheaves. It is needed to express Verdier duality in its most general form.-Definition:Let f: X →...
.
The exclamation mark
Exclamation mark
The exclamation mark, exclamation point, or bang, or "dembanger" is a punctuation mark usually used after an interjection or exclamation to indicate strong feelings or high volume , and often marks the end of a sentence. Example: “Watch out!” The character is encoded in Unicode at...
is often pronounced "shriek
Shriek
Shriek may refer to:* A kind of vociferation* a slang term for the exclamation mark, used in some computing and mathematical contexts, such as f_! and f^! being called shriek maps....
" (slang for exclamation mark), and the maps called "f shriek" or "f lower shriek" and "f upper shriek" – see also shriek map
Shriek map
In category theory, a branch of mathematics, certain unusual functors are denoted f_! and f^!, with the exclamation mark used to indicate that they are exceptional in some way...
.
Verdier duality
Global Verdier duality states that Rf! has a right adjoint f! in the derived category, in other words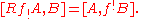
If X is a finite covering space of Y then f! takes sheaves to sheaves and is the same as f∗. If X is a closed subspace of Y then f! again takes sheaves to sheaves, but in general its image on sheaves cannot be represented by a single sheaf, but only by a complex of sheaves on the derived category.
Local Verdier duality states that
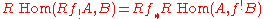
in the right derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of sheaves of F modules over X.
Taking homology of both sides gives global Verdier duality.
The dualizing complex DX on X is defined to be
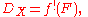
where f is the map from X to a point.
If X is a finite dimensional locally compact space, and Db(X) the bounded derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of sheaves of abelian groups over X, then the Verdier dual is a contravariant functor
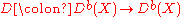
defined by

It has the following properties:
- D2(S) is isomorphic to S when S has constructible cohomology.
- (Verdier duality) If f is a continuous map from X to Y then there is an isomorphism
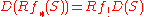
for any S ∈ Db(X).
Here Rf∗ denotes the higher direct image, at the derived category level.
In the special case when Y is a point and X is compact this says (roughly) that the cohomologies of dual complexes are dual.
Poincaré duality
Poincaré dualityPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
is a special case of Verdier duality; this can be seen as follows.
In the derived category, cohomology can be interpreted as chain homotopy classes of maps
- Hk (X, F) = [F[−k],X] = [F, X[k]]
where F[−k] is the complex with the constant sheaf
Constant sheaf
In mathematics, the constant sheaf on a topological space X associated to a set A is a sheaf of sets on X whose stalks are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset of X the value A, and all of whose restriction maps...
F concentrated in degree k, and [—, —] denote the chain homotopy classes of maps. The Verdier dual allows us to interpret homology in the derived category as well:
- [F[−k], DX] = Hk (X, F).
The left hand side is by definition the dual of the cohomology with compact support, so this equation says that homology is dual to cohomology with compact support.
It also follows that for an oriented manifold
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
M, the Verdier dual is given by
- DM = F[−n].
Ordinary Poincaré duality of a manifold can then be interpreted as the perfect pairing
- [F[−k], F] ⊗ [F[k−n], F[−n]] → [F[−n], F[−n]] → F.

