Uniform module
Encyclopedia
In abstract algebra
, a module is called a uniform module if the intersection of any two nonzero submodules is nonzero. This is equivalent to saying that every nonzero submodule of M is an essential submodule. A ring may be called a right (left) uniform ring if it is uniform as a right (left) module over itself.
Alfred Goldie
used the notion of uniform modules to construct a measure of dimension
for modules, now known as the uniform dimension (or Goldie dimension) of a module. Uniform dimension generalizes some, but not all, aspects of the notion of the dimension of a vector space. Finite uniform dimension was a key assumption for several theorems by Goldie, including Goldie's theorem
, which characterizes which rings are right orders in a semisimple ring. Modules of finite uniform dimension generalize both Artinian module
s and Noetherian module
s.
In the literature, uniform dimension is also referred to as simply the dimension of a module or the rank of a module. Uniform dimension should not be confused with the related notion, also due to Goldie, of the reduced rank of a module.
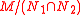fails to be uniform, as
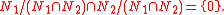
Uniserial modules are uniform, and uniform modules are necessarily directly indecomposable. Any commutative domain is a uniform ring, since if a and b are nonzero elements of two ideals, then the product ab is a nonzero element in the intersection of the ideals.
Theorem: If Ui and Vj are members of a finite collection of uniform submodules of a module M such that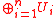
and 
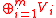are both essential submodules of M, then n = m.
The uniform dimension of a module M, denoted u.dim(M), is defined to be n if there exists a finite set of uniform submodules Ui such that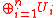
is an essential submodule of M. The preceding theorem ensures that this n is well defined. If no such finite set of submodules exists, then u.dim(M) is defined to be ∞. When speaking of the uniform dimension of a ring, it is necessary to specify whether u.dim(RR) or rather u.dim(RR) is being measured. It is possible to have two different uniform dimensions on the opposite sides of a ring.
If N is a submodule of M, then u.dim(N) ≤ u.dim(M) with equality exactly when N is an essential submodule of M. In particular, M and its injective hull
E(M) always have the same uniform dimension. It is also true that u.dim(M) = n if and only if E(M) is a direct sum of n indecomposable injective module
s.
It can be shown that u.dim(M) = ∞ if and only if M contains an infinite direct sum of nonzero submodules. Thus if M is either Noetherian or Artinian, M has finite uniform dimension. If M has finite composition length
k, then u.dim(M) ≤ k with equality exactly when M is a semisimple module
.
A standard result is that a right Noetherian domain is a right Ore domain. In fact, we can recover this result from another theorem attributed to Goldie, which states that the following three conditions are equivalent for a domain D:
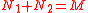, then either N1 = M or N2 = M. Equivalently one could also say that every proper submodule of M is a superfluous submodule.
These modules also admit an analogue of uniform dimension, called co-uniform dimension, corank, hollow dimension or dual Goldie dimension. The earliest studies of hollow modules and co-uniform dimension were initiated in , and . The reader is cautioned that these two authors explore distinct ways of dualizing Goldie dimension. Varadarajan's version of hollow dimension is arguably the more natural one.
It is always the case that a finitely cogenerated module has finite uniform dimension. This raises the question: does a finitely generated module have finite hollow dimension? The answer tunrs out to be no: in "Dual Goldie dimension II", Varadarajan showed that if a module M has finite hollow dimension, then M/J(M) is a semisimple
, Artinian module
. Since there are many rings with unity for which R/J(R) is not semisimple Artinian, we see that R is finitely generated but has infinite hollow dimension.
An additional surprising corollary of Varadarajan's result is that RR has finite hollow dimension exactly when RR does. This contrasts the finite uniform dimension case, since it is known a ring can have finite uniform dimension on one side and infinite uniform dimension on the other.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a module is called a uniform module if the intersection of any two nonzero submodules is nonzero. This is equivalent to saying that every nonzero submodule of M is an essential submodule. A ring may be called a right (left) uniform ring if it is uniform as a right (left) module over itself.
Alfred Goldie
Alfred Goldie
Alfred William Goldie was an English mathematician.Goldie was Assistant Lecturer, Nottingham University 1946-48; Lecturer, then Senior Lecturer, Newcastle University 1948-63; and Professor of Pure Mathematics, Leeds University 1963-86;He won the 1970 Senior Berwick Prize from the London...
used the notion of uniform modules to construct a measure of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
for modules, now known as the uniform dimension (or Goldie dimension) of a module. Uniform dimension generalizes some, but not all, aspects of the notion of the dimension of a vector space. Finite uniform dimension was a key assumption for several theorems by Goldie, including Goldie's theorem
Goldie's theorem
In mathematics, Goldie's theorem is a basic structural result in ring theory, proved by Alfred Goldie during the 1950s. What is now termed a right Goldie ring is a ring R that has finite uniform dimension as a right module over itself, and satisfies the ascending chain condition on right...
, which characterizes which rings are right orders in a semisimple ring. Modules of finite uniform dimension generalize both Artinian module
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
s and Noetherian module
Noetherian module
In abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
s.
In the literature, uniform dimension is also referred to as simply the dimension of a module or the rank of a module. Uniform dimension should not be confused with the related notion, also due to Goldie, of the reduced rank of a module.
Properties and examples of uniform modules
Being a uniform module is not usually preserved by direct products or quotient modules. The direct sum of two nonzero uniform modules always contains two submodules with intersection zero, namely the two original summand modules. If N1 and N2 are proper submodules of a uniform module M and neither submodule contains the other, then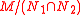 fails to be uniform, as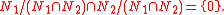Uniserial modules are uniform, and uniform modules are necessarily directly indecomposable. Any commutative domain is a uniform ring, since if a and b are nonzero elements of two ideals, then the product ab is a nonzero element in the intersection of the ideals.
Uniform dimension of a module
The following theorem makes it possible to define a dimension on modules using uniform submodules. It is a module version of a vector space theorem:Theorem: If Ui and Vj are members of a finite collection of uniform submodules of a module M such that
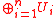and 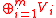are both essential submodules of M, then n = m.The uniform dimension of a module M, denoted u.dim(M), is defined to be n if there exists a finite set of uniform submodules Ui such that
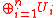is an essential submodule of M. The preceding theorem ensures that this n is well defined. If no such finite set of submodules exists, then u.dim(M) is defined to be ∞. When speaking of the uniform dimension of a ring, it is necessary to specify whether u.dim(RR) or rather u.dim(RR) is being measured. It is possible to have two different uniform dimensions on the opposite sides of a ring.If N is a submodule of M, then u.dim(N) ≤ u.dim(M) with equality exactly when N is an essential submodule of M. In particular, M and its injective hull
Injective hull
In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
E(M) always have the same uniform dimension. It is also true that u.dim(M) = n if and only if E(M) is a direct sum of n indecomposable injective module
Injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
s.
It can be shown that u.dim(M) = ∞ if and only if M contains an infinite direct sum of nonzero submodules. Thus if M is either Noetherian or Artinian, M has finite uniform dimension. If M has finite composition length
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
k, then u.dim(M) ≤ k with equality exactly when M is a semisimple module
Semisimple module
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
.
A standard result is that a right Noetherian domain is a right Ore domain. In fact, we can recover this result from another theorem attributed to Goldie, which states that the following three conditions are equivalent for a domain D:
- D is right Ore
- u.dim(DD) = 1
- u.dim(DD) < ∞
Hollow modules and co-uniform dimension
The dual notion of a uniform module is that of a hollow module: a module M is said to be hollow if when N1 and N2 are submodules of M such that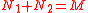, then either N1 = M or N2 = M. Equivalently one could also say that every proper submodule of M is a superfluous submodule.These modules also admit an analogue of uniform dimension, called co-uniform dimension, corank, hollow dimension or dual Goldie dimension. The earliest studies of hollow modules and co-uniform dimension were initiated in , and . The reader is cautioned that these two authors explore distinct ways of dualizing Goldie dimension. Varadarajan's version of hollow dimension is arguably the more natural one.
It is always the case that a finitely cogenerated module has finite uniform dimension. This raises the question: does a finitely generated module have finite hollow dimension? The answer tunrs out to be no: in "Dual Goldie dimension II", Varadarajan showed that if a module M has finite hollow dimension, then M/J(M) is a semisimple
Semisimple module
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
, Artinian module
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
. Since there are many rings with unity for which R/J(R) is not semisimple Artinian, we see that R is finitely generated but has infinite hollow dimension.
An additional surprising corollary of Varadarajan's result is that RR has finite hollow dimension exactly when RR does. This contrasts the finite uniform dimension case, since it is known a ring can have finite uniform dimension on one side and infinite uniform dimension on the other.