Ugly duckling theorem
Encyclopedia
The Ugly Duckling theorem is an argument
asserting that classification is impossible without some sort of bias
. It is named for Hans Christian Andersen
's famous story of "The Ugly Duckling
." It gets its name because it shows that, all things being equal, an ugly duckling is just as similar to a swan
as two swans are to each other, although it is only a theorem
in a very informal sense. It was proposed by Satosi Watanabe in 1969.
es about what sorts of categories are "natural" or "normal" and what are not. So one has to consider all the possible classes that could be, all the possible ways of making sets out of the n objects. There are
such ways, the size of the power set of n objects. One can use that to measure the similarity between two objects: and one would see how many sets they have in common. However one can not. Any two objects have exactly the same number of classes in common if they are only distinguished by their names with one another, namely 
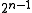(half the total number of classes there are). To see this is so, one may imagine each class is a represented by an n-bit string (or binary encoded
integer), with a zero for each element not in the class and a one for each element in the class. As one finds, there are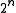
such strings.
As all possible choices of zeros and ones are there, any two bit-positions will agree exactly half the time. One may pick two elements and reorder the bits so they are the first two, and imagine the numbers sorted lexicographically. The first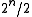
numbers will have bit #1 set to zero, and the second 
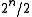will have it set to one. Within each of those blocks, the top 
will have bit #2 set to zero and the other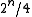 
will have it as one, so they agree on two blocks of 
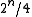or on half of all the cases. No matter which two elements one picks. So if we have no preconceived bias about which categories are better, everything is then equally similar (or equally dissimilar). The number of predicates
simultaneously satisfied by two non-identical elements is constant over all such pairs and is the same as the number of those satisfied by one. Thus, some kind of inductive bias is needed to make judgements; i.e. to prefer certain categories over others.
(A possible way to proceed is however correspondence analysis
).
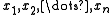be a set of vectors of 
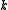booleans each. The ugly duckling is the vector which is least like the others. Given the booleans, this can be computed using Hamming distance.
However, the choice of boolean features to consider could have been somewhat arbitrary. Perhaps there were features derivable from the original features that were important for identifying the ugly duckling. The set of booleans in the vector can be extended with new features computed as boolean functions of the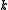
original features. The only canonical way to do this is to extend it with all possible Boolean functions. The resulting completed vectors have 
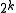features. The Ugly Duckling Theorem states that there is no ugly duckling because any two completed vectors will either be equal or differ in exactly half of the features.
Proof. Let x and y be two vectors. If they are the same, then their completed vectors must also be the same because any Boolean function of x will agree with the same Boolean function of y. If x and y are different, then there exists a coordinate
where the 
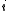-th coordinate of 
differs from the 
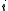-th coordinate of 
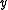. Now the completed features contain every Boolean function on 
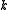Boolean variables, with each one exactly once. Viewing these Boolean functions as polynomials in 
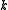variables over GF(2), segregate the functions into pairs 
where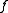 
contains the 
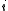-th coordinate as a linear term and 
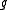is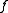 
without that linear term. Now, for every such pair 
, 
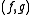and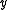 
will agree on exactly one of the two functions. If they agree on one, they must disagree on the other and vice versa. (This proof is believed to be due to Watanabe.)
Argument
In philosophy and logic, an argument is an attempt to persuade someone of something, or give evidence or reasons for accepting a particular conclusion.Argument may also refer to:-Mathematics and computer science:...
asserting that classification is impossible without some sort of bias
Bias (statistics)
A statistic is biased if it is calculated in such a way that it is systematically different from the population parameter of interest. The following lists some types of, or aspects of, bias which should not be considered mutually exclusive:...
. It is named for Hans Christian Andersen
Hans Christian Andersen
Hans Christian Andersen was a Danish author, fairy tale writer, and poet noted for his children's stories. These include "The Steadfast Tin Soldier," "The Snow Queen," "The Little Mermaid," "Thumbelina," "The Little Match Girl," and "The Ugly Duckling."...
's famous story of "The Ugly Duckling
The Ugly Duckling
"The Ugly Duckling" is a literary fairy tale by Danish poet and author Hans Christian Andersen . The story tells of a homely little bird born in a barnyard who suffers abuse from his neighbors until, much to his delight , he matures into a beautiful swan, the most beautiful bird of all...
." It gets its name because it shows that, all things being equal, an ugly duckling is just as similar to a swan
Swan
Swans, genus Cygnus, are birds of the family Anatidae, which also includes geese and ducks. Swans are grouped with the closely related geese in the subfamily Anserinae where they form the tribe Cygnini. Sometimes, they are considered a distinct subfamily, Cygninae...
as two swans are to each other, although it is only a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in a very informal sense. It was proposed by Satosi Watanabe in 1969.
Basic idea
Suppose there are n things in the universe, and one wants to put them into classes or categories. One has no preconceived ideas or biasBias
Bias is an inclination to present or hold a partial perspective at the expense of alternatives. Bias can come in many forms.-In judgement and decision making:...
es about what sorts of categories are "natural" or "normal" and what are not. So one has to consider all the possible classes that could be, all the possible ways of making sets out of the n objects. There are
such ways, the size of the power set of n objects. One can use that to measure the similarity between two objects: and one would see how many sets they have in common. However one can not. Any two objects have exactly the same number of classes in common if they are only distinguished by their names with one another, namely 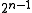(half the total number of classes there are). To see this is so, one may imagine each class is a represented by an n-bit string (or binary encodedBinary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
integer), with a zero for each element not in the class and a one for each element in the class. As one finds, there are
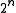such strings.As all possible choices of zeros and ones are there, any two bit-positions will agree exactly half the time. One may pick two elements and reorder the bits so they are the first two, and imagine the numbers sorted lexicographically. The first
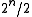numbers will have bit #1 set to zero, and the second 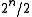will have it set to one. Within each of those blocks, the top will have bit #2 set to zero and the other 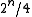will have it as one, so they agree on two blocks of 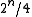or on half of all the cases. No matter which two elements one picks. So if we have no preconceived bias about which categories are better, everything is then equally similar (or equally dissimilar). The number of predicatesPropositional function
A propositional function in logic, is a statement expressed in a way that would assume the value of true or false, except that within the statement is a variable that is not defined or specified, which leaves the statement undetermined...
simultaneously satisfied by two non-identical elements is constant over all such pairs and is the same as the number of those satisfied by one. Thus, some kind of inductive bias is needed to make judgements; i.e. to prefer certain categories over others.
(A possible way to proceed is however correspondence analysis
Correspondence analysis
Correspondence analysis is a multivariate statistical technique proposed by Hirschfeld and later developed by Jean-Paul Benzécri. It is conceptually similar to principal component analysis, but applies to categorical rather than continuous data...
).
As a statement about Boolean functions
Let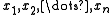 be a set of vectors of 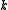booleans each. The ugly duckling is the vector which is least like the others. Given the booleans, this can be computed using Hamming distance.However, the choice of boolean features to consider could have been somewhat arbitrary. Perhaps there were features derivable from the original features that were important for identifying the ugly duckling. The set of booleans in the vector can be extended with new features computed as boolean functions of the
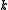original features. The only canonical way to do this is to extend it with all possible Boolean functions. The resulting completed vectors have 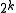features. The Ugly Duckling Theorem states that there is no ugly duckling because any two completed vectors will either be equal or differ in exactly half of the features.Proof. Let x and y be two vectors. If they are the same, then their completed vectors must also be the same because any Boolean function of x will agree with the same Boolean function of y. If x and y are different, then there exists a coordinate
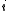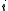where the -th coordinate of differs from the -th coordinate of 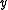. Now the completed features contain every Boolean function on 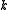Boolean variables, with each one exactly once. Viewing these Boolean functions as polynomials in 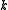variables over GF(2), segregate the functions into pairs where 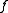contains the 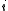-th coordinate as a linear term and 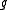is 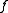without that linear term. Now, for every such pair 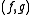, and 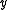will agree on exactly one of the two functions. If they agree on one, they must disagree on the other and vice versa. (This proof is believed to be due to Watanabe.)