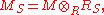Torsion (abstract algebra)
Encyclopedia
In abstract algebra
, the term torsion refers to a number of concepts related to elements of finite order in groups
and to the failure of modules
to be free
.
. An element g of G is called a torsion element if g has finite order
. If all elements of G are torsion elements, then G is called a torsion group. If the only torsion element is the identity element
, then the group G is called torsion-free.
Let M be a module over a ring
R without zero divisor
s. An element m of M is called a torsion element if the cyclic submodule of M generated by m is not free
. Equivalently, m is torsion if and only if it has a non-zero annihilator
in R. If the ring R is an integral domain, then the set of all torsion elements forms a submodule of M, called the torsion submodule of M, sometimes denoted T(M). The module M is called a torsion module if T(M) = M, and is called torsion-free if T(M) = 0. Note that when R is only a commutative ring, torsion elements of M might not form a submodule.
If the ring R is non-commutative then the situation is more complicated, and the set of torsion elements need not be a submodule. Nevertheless, it is a submodule given the assumption that the ring R satisfies the Ore condition
. This covers the case when R is a Noetherian
domain
.
Any abelian group
may be viewed as a module over the ring Z of integer
s, and in this case the two notions of torsion coincide.
More generally, let R be an arbitrary ring and S ⊂ R be a multiplicatively closed subset. Then one defines the notion of S-torsion as follows. An element m of an R-module M is called an S-torsion element if there exists s in S such that s annihilates
m, i.e., sm = 0. In particular, one can take for S to be the set of all non-zero divisors of the ring R. In this case, S-torsion is frequently called simply torsion, extending the definition above from the case of domains
to general rings.
over any ring R. Then it follows immediately from the definitions that M is torsion-free (if the ring R is not a domain then torsion is considered with respect to the set S of non-zero divisors of R). In particular, any free abelian group
is torsion-free and any vector space
over a field K is torsion-free when viewed as the module over K.
2. By contrast with Example 1, any finite group
(abelian or not) is periodic and finitely generated.
Burnside's problem
asks whether, conversely, any finitely generated periodic group must be finite.
(The answer is "no" in general, even if the period is fixed.)
3. In the modular group
, Γ obtained from the group SL(2,Z) of two by two integer matrices with unit determinant by factoring out its center, any nontrivial torsion element either has order two and is conjugate to the element S or has order three and is conjugate to the element ST. In this case, torsion elements do not form a subgroup, for example, S · ST = T, which has infinite order.
4. The abelian group Q/Z, consisting of the rational numbers (mod 1), is periodic, i.e. every element has finite order. Analogously, the module K(t)/K[t] over the ring R = K[t] of polynomial
s in one variable is pure torsion. Both these examples can be generalized as follows: if R is a commutative domain and Q is its field of fractions, then Q/R is a torsion R-module.
5. The torsion subgroup of (R/Z,+) is (Q/Z,+) while the groups (R,+),(Z,+) are torsion-free. The quotient of a torsion-free abelian group by a subgroup is torsion-free exactly when the subgroup is a pure subgroup
.
and M is a finitely-generated R-module
. Then the structure theorem for finitely generated modules over a principal ideal domain
gives a detailed description of the module M up to isomorphism. In particular, it claims that
where F is a free R-module of finite rank (depending only on M) and T(M) is the torsion submodule of M. As a corollary, any finitely-generated torsion-free module over R is free. This corollary does not hold for more general commutative domains, even for R = K[x,y], the ring of polynomials in two variables.
For non-finitely generated modules, the above direct decomposition is not true. The torsion subgroup of an abelian group may not be a direct summand of it.
obtained from M by extension of scalars
. Since Q is a field
, a module over Q is a vector space
, possibly, infinite-dimensional. There is a canonical homomorphism of abelian groups from M to MQ, and the kernel
of this homomorphism is precisely the torsion submodule T(M). More generally, if S is a multiplicatively closed subset of the ring R, then we may consider localization of the R-module M,
which is a module over the localization
RS. There is a canonical map from M to MS, whose kernel is precisely the S-torsion submodule of M.
Thus the torsion submodule of M can be interpreted as the set of the elements that 'vanish in the localization'. The same interpretation continues to hold in the non-commutative setting for rings satisfying the Ore condition, or more generally for any right denominator set S and right R-module M.
. If M and N are two modules over a commutative ring R (for example, two abelian groups, when R = Z), Tor functor
s yield a family of R-modules Tori(M,N). The S-torsion of an R-module M is canonically isomorphic to Tor1(M, RS/R). The symbol Tor denoting the functors reflects this relation with the algebraic torsion. This same result holds for non-commutative rings as well as long as the set S is a right denominator set.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the term torsion refers to a number of concepts related to elements of finite order in groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and to the failure of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
to be free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
.
Definition
Let G be a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. An element g of G is called a torsion element if g has finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
. If all elements of G are torsion elements, then G is called a torsion group. If the only torsion element is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, then the group G is called torsion-free.
Let M be a module over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R without zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s. An element m of M is called a torsion element if the cyclic submodule of M generated by m is not free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
. Equivalently, m is torsion if and only if it has a non-zero annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
in R. If the ring R is an integral domain, then the set of all torsion elements forms a submodule of M, called the torsion submodule of M, sometimes denoted T(M). The module M is called a torsion module if T(M) = M, and is called torsion-free if T(M) = 0. Note that when R is only a commutative ring, torsion elements of M might not form a submodule.
If the ring R is non-commutative then the situation is more complicated, and the set of torsion elements need not be a submodule. Nevertheless, it is a submodule given the assumption that the ring R satisfies the Ore condition
Ore condition
In mathematics, especially in the area of algebra known as ring theory, the Ore condition is a condition introduced by Øystein Ore, in connection with the question of extending beyond commutative rings the construction of a field of fractions, or more generally localization of a ring...
. This covers the case when R is a Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
.
Any abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
may be viewed as a module over the ring Z of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, and in this case the two notions of torsion coincide.
More generally, let R be an arbitrary ring and S ⊂ R be a multiplicatively closed subset. Then one defines the notion of S-torsion as follows. An element m of an R-module M is called an S-torsion element if there exists s in S such that s annihilates
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
m, i.e., sm = 0. In particular, one can take for S to be the set of all non-zero divisors of the ring R. In this case, S-torsion is frequently called simply torsion, extending the definition above from the case of domains
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
to general rings.
Examples
1. Let M be a free moduleFree module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
over any ring R. Then it follows immediately from the definitions that M is torsion-free (if the ring R is not a domain then torsion is considered with respect to the set S of non-zero divisors of R). In particular, any free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
is torsion-free and any vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field K is torsion-free when viewed as the module over K.
2. By contrast with Example 1, any finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
(abelian or not) is periodic and finitely generated.
Burnside's problem
Burnside's problem
The Burnside problem, posed by William Burnside in 1902 and one of the oldest and most influential questions in group theory, asks whether a finitely generated group in which every element has finite order must necessarily be a finite group...
asks whether, conversely, any finitely generated periodic group must be finite.
(The answer is "no" in general, even if the period is fixed.)
3. In the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, Γ obtained from the group SL(2,Z) of two by two integer matrices with unit determinant by factoring out its center, any nontrivial torsion element either has order two and is conjugate to the element S or has order three and is conjugate to the element ST. In this case, torsion elements do not form a subgroup, for example, S · ST = T, which has infinite order.
4. The abelian group Q/Z, consisting of the rational numbers (mod 1), is periodic, i.e. every element has finite order. Analogously, the module K(t)/K[t] over the ring R = K[t] of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in one variable is pure torsion. Both these examples can be generalized as follows: if R is a commutative domain and Q is its field of fractions, then Q/R is a torsion R-module.
5. The torsion subgroup of (R/Z,+) is (Q/Z,+) while the groups (R,+),(Z,+) are torsion-free. The quotient of a torsion-free abelian group by a subgroup is torsion-free exactly when the subgroup is a pure subgroup
Pure subgroup
In mathematics, especially in the area of algebra studying the theory of abelian groups, a pure subgroup is a generalization of direct summand. It has found many uses in abelian group theory and related areas.-Definition:...
.
Case of a principal ideal domain
Suppose that R is a (commutative) principal ideal domainPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
and M is a finitely-generated R-module
Finitely-generated module
In mathematics, a finitely generated module is a module that has a finite generating set. A finitely generated R-module also may be called a finite R-module or finite over R....
. Then the structure theorem for finitely generated modules over a principal ideal domain
Structure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
gives a detailed description of the module M up to isomorphism. In particular, it claims that
where F is a free R-module of finite rank (depending only on M) and T(M) is the torsion submodule of M. As a corollary, any finitely-generated torsion-free module over R is free. This corollary does not hold for more general commutative domains, even for R = K[x,y], the ring of polynomials in two variables.
For non-finitely generated modules, the above direct decomposition is not true. The torsion subgroup of an abelian group may not be a direct summand of it.
Torsion and localization
Assume that R is a commutative domain and M is an R-module. Let Q be the quotient field of the ring R. Then one can consider the Q-moduleobtained from M by extension of scalars
Extension of scalars
In abstract algebra, extension of scalars is a means of producing a module over a ring S from a module over another ring R, given a homomorphism f : R \to S between them...
. Since Q is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, a module over Q is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, possibly, infinite-dimensional. There is a canonical homomorphism of abelian groups from M to MQ, and the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of this homomorphism is precisely the torsion submodule T(M). More generally, if S is a multiplicatively closed subset of the ring R, then we may consider localization of the R-module M,
which is a module over the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
RS. There is a canonical map from M to MS, whose kernel is precisely the S-torsion submodule of M.
Thus the torsion submodule of M can be interpreted as the set of the elements that 'vanish in the localization'. The same interpretation continues to hold in the non-commutative setting for rings satisfying the Ore condition, or more generally for any right denominator set S and right R-module M.
Torsion in homological algebra
The concept of torsion plays an important role in homological algebraHomological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
. If M and N are two modules over a commutative ring R (for example, two abelian groups, when R = Z), Tor functor
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
s yield a family of R-modules Tori(M,N). The S-torsion of an R-module M is canonically isomorphic to Tor1(M, RS/R). The symbol Tor denoting the functors reflects this relation with the algebraic torsion. This same result holds for non-commutative rings as well as long as the set S is a right denominator set.
See also
- Analytic torsionAnalytic torsionIn mathematics, Reidemeister torsion is a topological invariant of manifolds introduced by Kurt Reidemeister for 3-manifolds and generalized to higher dimensions by and ....
- Arithmetic dynamicsArithmetic dynamicsArithmetic dynamicsis a field that amalgamates two areas of mathematics, dynamical systems and number theory.Classically, discrete dynamics refers to the study of the iteration of self-maps of the complex plane or real line...
- Flat moduleFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
- Localization of a module
- Rank of an abelian groupRank of an abelian groupIn mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
- Ray-Singer torsion
- Universal coefficient theoremUniversal coefficient theoremIn mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...