
Tent map
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
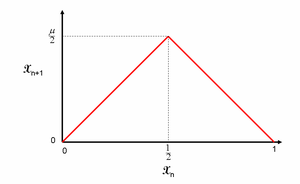
, the tent map with parameter μ is the real-valued function fμ defined by

the name being due to the tent
Tent
A tent is a shelter consisting of sheets of fabric or other material draped over or attached to a frame of poles or attached to a supporting rope. While smaller tents may be free-standing or attached to the ground, large tents are usually anchored using guy ropes tied to stakes or tent pegs...
-like shape of the graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
of fμ. For the values of the parameter μ within 0 and 2, fμ maps
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1] into itself, thus
defining a discrete-time dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
on it (equivalently, a recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
). In particular, iterating
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
a point x0 in [0, 1] gives rise to a sequence
 :
:
where μ is a positive real constant. Choosing for instance the parameter μ=2 , the effect of the function fμ may be viewed as the result of the operation of folding the unit interval in two, then stretching the resulting interval [0,1/2] to get again the interval [0,1]. Iterating the procedure, any point x0 of the interval assumes new subsequent positions as described above, generating a sequence xn in [0,1].
The
 case of the tent map is a non-linear transformation of both the bit shift map and the r=4 case of the logistic map
case of the tent map is a non-linear transformation of both the bit shift map and the r=4 case of the logistic mapLogistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
.
Behaviour
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
are topologically conjugate , and thus the behaviours of the two maps are in this sense identical under iteration.
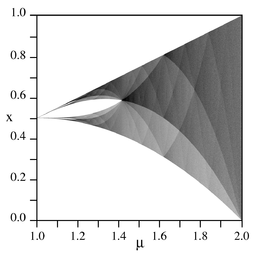
Depending on the value of μ, the tent map demonstrates a range of dynamical behaviour ranging from predictable to chaotic.
- If μ is less than 1 the point x = 0 is an attractiveAttractorAn attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of the system for all initial values of x i.e. the system will converge towards x = 0 from any initial value of x.
- If μ is 1 all values of x less than or equal to 1/2 are fixed points of the system.
- If μ is greater than 1 the system has two fixed points, one at 0, and the other at μ/(μ + 1). Both fixed points are unstable i.e. a value of x close to either fixed point will move away from it, rather than towards it. For example, when μ is 1.5 there is a fixed point at x = 0.6 (because 1.5(1 − 0.6) = 0.6) but starting at x = 0.61 we get
- If μ is between 1 and the square root of 2 the system maps a set of intervals between μ − μ2/2 and μ/2 to themselves. This set of intervals is the Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
of the map i.e. it is the smallest invariant sub-set of the real line under this map. If μ is greater than the square root of 2, these intervals merge, and the Julia set is the whole interval from μ − μ2/2 to μ/2 (see bifurcation diagram).
- If μ is between 1 and 2 the interval [μ − μ2/2, μ/2]contains both periodic and non-periodic points, although all of the orbitOrbit (dynamics)In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
s are unstable (i.e. nearby points move away from the orbits rather than towards them). Orbits with longer lengths appear as μ increases. For example:
- If μ equals 2 the system maps the interval [0,1] onto itself. There are now periodic points with every orbit length within this interval, as well as non-periodic points. The periodic points are denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in [0,1], so the map has become chaoticChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
. In fact, the dynamics will be non-periodic if and only if is irrational. This can be seen by noting what the map does when
is irrational. This can be seen by noting what the map does when  is expressed in binary notation: It shifts the binary point one place to the right; then, if what appears to the left of the binary point is a "one" it changes all ones to zeroes and vice versa (with the exception of the final bit "one" in the case of a finite binary expansion); starting from an irrational number, this process goes on forever without repeating itself. The invariant measure for x is the uniform density over the unit interval. The autocorrelation function for a sufficiently long sequence {
is expressed in binary notation: It shifts the binary point one place to the right; then, if what appears to the left of the binary point is a "one" it changes all ones to zeroes and vice versa (with the exception of the final bit "one" in the case of a finite binary expansion); starting from an irrational number, this process goes on forever without repeating itself. The invariant measure for x is the uniform density over the unit interval. The autocorrelation function for a sufficiently long sequence { } will show zero autocorrelation at all non-zero lags. Thus
} will show zero autocorrelation at all non-zero lags. Thus  cannot be distinguished from white noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
cannot be distinguished from white noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
using the autocorrelation function. Note that the r=4 case of the logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
and the case of the tent map are transformations of each other: Denoting the logistically evolving variable as
case of the tent map are transformations of each other: Denoting the logistically evolving variable as  , we have
, we have  .
.
- If μ is greater than 2 the map's Julia set becomes disconnected, and breaks up into a Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
within the interval [0,1]. The Julia set still contains an infinite number of both non-periodic and periodic points (including orbits for any orbit length) but almost everyAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
point within [0,1] will now eventually diverge towards infinity. The canonical Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
(obtained by successively deleting middle thirds from subsets of the unit line) is the Julia set of the tent map for μ = 3.
Magnifying the orbit diagram
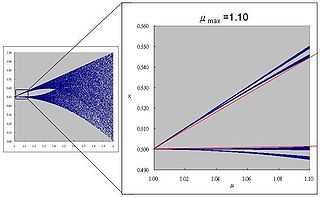
- A closer look at the orbit diagram shows that there are 4 separated regions at μ ≈ 1. For further magnification, 2 reference lines (red) are drawn from the tip to suitable x at certain μ (e.g., 1.10) as shown.
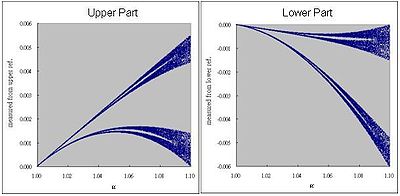
- With distance measured from the corresponding reference lines, further detail appears in the upper and lower part of the map. (total 8 separated regions at some μ)
Asymmetric tent map
The asymmetric tent map is essentially a distorted, but still piecewise linear, version of the case of the tent map. It is defined by
case of the tent map. It is defined by
for parameter
 . The
. The  case of the tent map is the present case of
case of the tent map is the present case of  . A sequence {
. A sequence { } will have the same autocorrelation function as will data from the first-order autoregressive process
} will have the same autocorrelation function as will data from the first-order autoregressive process  with {
with { } independently and identically distributed. Thus data from an asymmetric tent map cannot be distinguished, using the autocorrelation function, from data generated by a first-order autoregressive process.
} independently and identically distributed. Thus data from an asymmetric tent map cannot be distinguished, using the autocorrelation function, from data generated by a first-order autoregressive process.





