Sylvester–Gallai theorem
Encyclopedia
The Sylvester–Gallai theorem asserts that given a finite number of points in the Euclidean plane, either
This claim was posed as a problem by . suggests that Sylvester may have been motivated by a related phenomenon in algebraic geometry
, in which the inflection point
s of a cubic curve in the complex projective plane form a configuration
of nine points and twelve lines in which each line determined by two of the points contains a third point. The Sylvester–Gallai theorem implies that it is impossible for all nine of these points to have real coordinates. proved the projective dual of this theorem, (actually, of a slightly stronger result). Unaware of Melchior's proof, again stated the conjecture, which was proved first by Tibor Gallai
, and soon afterwards by other authors.
A line that contains exactly two of a set of points is known as an ordinary line. There is an algorithm
that finds an ordinary line in a set of n points in time proportional to n log n in the worst case.
The Sylvester–Gallai theorem does not apply to sets of infinitely many points: all points in the plane or in the unit disk are obvious counterexample
s. For countable
counterexamples, consider for instance the lattice of integer points
, or all rational points in the unit disc. As the example of the inflection points of a cubic curve shows, the Sylvester–Gallai theorem also does not apply to the complex projective plane.
RP2 instead of the Euclidean plane. This provides no additional generality, as any finite set of projective points can be transformed into a Euclidean point set preserving all ordinary lines; but the projective viewpoint allows certain configurations to be described more easily.
By projective duality, the existence of an ordinary line in a set of non-collinear points in RP2 is equivalent to the existence of an ordinary point in a nontrivial arrangement
of finitely many lines. An arrangement is said to be trivial when all its lines pass through a common point, and nontrivial otherwise; an ordinary point is a point that belongs to exactly two lines.
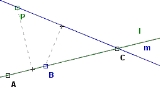
For a description of Gallai's original proof of the theorem, see e.g. . The proof below is instead due to Kelly.
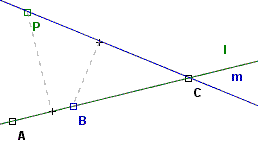
Suppose for contradiction that we have a finite set of points not all collinear but with at least three points on each line. Call it S. Define a connecting line to be a line which contains at least two points in the collection. Let (P,l) be the point and connecting line that are the smallest positive distance apart among all point-line pairs.
By the supposition, the connecting line l goes through at least three points of S, so dropping a perpendicular from P to l there must be at least two points on one side of the perpendicular (one might be exactly on the intersection of the perpendicular with l). Call the point closer to the perpendicular B, and the farther point C. Draw the line m connecting P to C. Then the distance from B to m is smaller than the distance from P to l, contradicting the original definition of P and l. One way to see this is to notice that the right triangle with hypotenuse BC is similar to and contained in the right triangle with hypotenuse PC.
Thus there cannot be a smallest positive distance between point-line pairs—every point must be distance 0 from every line. In other words, every point must lie on the same line if each connecting line has at least three points.
Melchior observed that, for any graph embedded
in RP2, the formula V − E + F must equal 1, the Euler characteristic
of RP2; where V, E, and F, are the number of vertices, edges, and faces of the graph, respectively. Any nontrivial line arrangement on RP2 defines a graph in which each face is bounded by at least three edges, and each edge bounds two faces; so, double counting
gives the additional inequality F ≤ 2E/3. Using this inequality to eliminate F from the Euler characteristic leads to the inequality E ≤ 3V − 3. But if every vertex in the arrangement were the crossing point of three or more lines, then the total number of edges would be at least 3V, contradicting this inequality. Therefore, some vertices must be the crossing point of only two lines, and as Melchior's more careful analysis shows, at least three ordinary vertices are needed in order to satisfy the inequality E ≤ 3V − 3.

Equivalently,
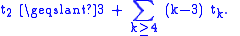
This is often referred to as Melchior's inequality.
, an axiomatization of geometry that includes not only Euclidean geometry but several other related geometries. See for minimal axiom systems inside which the Sylvester–Gallai theorem can be proved.
 While the Sylvester–Gallai theorem tells us that an arrangement of points, not all collinear, must determine an ordinary line, it does not say how many must be determined.
While the Sylvester–Gallai theorem tells us that an arrangement of points, not all collinear, must determine an ordinary line, it does not say how many must be determined.
Let be the minimum number of ordinary lines determined over every set of n non-collinear points. Melchior's proof showed that raised the question of whether approaches infinity with n. confirmed this conjecture by proving that conjectured that for all values of n, a conjecture that still stands . This is often referred to as the Dirac-Motzkin conjecture, see for example . proved that t2(n) ≥ 3n/7.
Dirac's conjectured lower bound is asymptotically the best possible, since there is a proven matching upper bound for even n greater than four. The construction, due to Károly Böröczky, that achieves this bound consists of the vertices of a regular m-gon in the real projective plane
and another m points (thus) on the line at infinity corresponding to each of the directions determined by pairs of vertices; although there are pairs, they determine only m distinct directions. This arrangement has only m ordinary lines, namely those that connect a vertex v with the point at infinity corresponding to the line determined by vs two neighboring vertices. Note that, as with any finite configuration in the real projective plane, this construction can be perturbed so that all points are finite, without changing the number of ordinary lines.
For odd n, only two examples are known that match Dirac's lower bound conjecture, that is, with One example, by , consists of the vertices, edge midpoints, and centroid of an equilateral triangle; these seven points determine only three ordinary lines. The configuration in which these three ordinary lines are replaced by a single line cannot be realized in the Euclidean plane, but forms a finite projective space
known as the Fano plane
. The other counterexample, due to McKee, consists of two regular pentagons joined edge-to-edge together with the midpoint of the shared edge and four points on the line at infinity in the projective plane
; these 13 points have among them 6 ordinary lines.
, the best proven lower bound for t2(n) was obtained by who proved that except when n is seven. Asymptotically, this formula is already 12/13 ~ 92.3% of the proven n/2 upper bound. The n = 7 case is an exception because otherwise the Kelly–Moser construction would be a counterexample; their construction shows that t2(7) ≤ 3. However, were the Csima–Sawyer bound valid for n = 7, it would claim that t2(7) ≥ 4.
A closely related result is Beck's theorem
, stating a tradeoff between the number of lines with few points and the number of points on a single line.
- all the points are collinearLine (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
; or - there is a line which contains exactly two of the points.
This claim was posed as a problem by . suggests that Sylvester may have been motivated by a related phenomenon in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, in which the inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s of a cubic curve in the complex projective plane form a configuration
Configuration (geometry)
In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.Although certain specific...
of nine points and twelve lines in which each line determined by two of the points contains a third point. The Sylvester–Gallai theorem implies that it is impossible for all nine of these points to have real coordinates. proved the projective dual of this theorem, (actually, of a slightly stronger result). Unaware of Melchior's proof, again stated the conjecture, which was proved first by Tibor Gallai
Tibor Gallai
Tibor Gallai was a Hungarian mathematician. He worked in combinatorics, especially in graph theory, and was a lifelong friend and collaborator of Paul Erdős. He was a student of Dénes König and an advisor of László Lovász...
, and soon afterwards by other authors.
A line that contains exactly two of a set of points is known as an ordinary line. There is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that finds an ordinary line in a set of n points in time proportional to n log n in the worst case.
The Sylvester–Gallai theorem does not apply to sets of infinitely many points: all points in the plane or in the unit disk are obvious counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
s. For countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
counterexamples, consider for instance the lattice of integer points
Square lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
, or all rational points in the unit disc. As the example of the inflection points of a cubic curve shows, the Sylvester–Gallai theorem also does not apply to the complex projective plane.
Projective and dual versions
The question of the existence of an ordinary line can also be posed for points in the real projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
RP2 instead of the Euclidean plane. This provides no additional generality, as any finite set of projective points can be transformed into a Euclidean point set preserving all ordinary lines; but the projective viewpoint allows certain configurations to be described more easily.
By projective duality, the existence of an ordinary line in a set of non-collinear points in RP2 is equivalent to the existence of an ordinary point in a nontrivial arrangement
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
of finitely many lines. An arrangement is said to be trivial when all its lines pass through a common point, and nontrivial otherwise; an ordinary point is a point that belongs to exactly two lines.
Kelly's proof

For a description of Gallai's original proof of the theorem, see e.g. . The proof below is instead due to Kelly.
Suppose for contradiction that we have a finite set of points not all collinear but with at least three points on each line. Call it S. Define a connecting line to be a line which contains at least two points in the collection. Let (P,l) be the point and connecting line that are the smallest positive distance apart among all point-line pairs.
By the supposition, the connecting line l goes through at least three points of S, so dropping a perpendicular from P to l there must be at least two points on one side of the perpendicular (one might be exactly on the intersection of the perpendicular with l). Call the point closer to the perpendicular B, and the farther point C. Draw the line m connecting P to C. Then the distance from B to m is smaller than the distance from P to l, contradicting the original definition of P and l. One way to see this is to notice that the right triangle with hypotenuse BC is similar to and contained in the right triangle with hypotenuse PC.
Thus there cannot be a smallest positive distance between point-line pairs—every point must be distance 0 from every line. In other words, every point must lie on the same line if each connecting line has at least three points.
Melchior's proof
In 1940, therefore prior to Gallai's proof, Melchior showed that any nontrivial finite arrangement of lines in the projective plane has at least three ordinary points. By duality, this results also says that any finite nontrvial set of points on the plane has at least three ordinary lines.Melchior observed that, for any graph embedded
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
in RP2, the formula V − E + F must equal 1, the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of RP2; where V, E, and F, are the number of vertices, edges, and faces of the graph, respectively. Any nontrivial line arrangement on RP2 defines a graph in which each face is bounded by at least three edges, and each edge bounds two faces; so, double counting
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
gives the additional inequality F ≤ 2E/3. Using this inequality to eliminate F from the Euler characteristic leads to the inequality E ≤ 3V − 3. But if every vertex in the arrangement were the crossing point of three or more lines, then the total number of edges would be at least 3V, contradicting this inequality. Therefore, some vertices must be the crossing point of only two lines, and as Melchior's more careful analysis shows, at least three ordinary vertices are needed in order to satisfy the inequality E ≤ 3V − 3.
Melchior's inequality
By a similar argument, Melchior was able to prove a more general result. For every k ≥ 2, let tk be the number of points to which k lines are incident. Then
Equivalently,
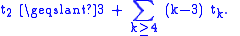
This is often referred to as Melchior's inequality.
Coxeter's proof
gave another proof of the Sylvester–Gallai theorem within ordered geometryOrdered geometry
Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement...
, an axiomatization of geometry that includes not only Euclidean geometry but several other related geometries. See for minimal axiom systems inside which the Sylvester–Gallai theorem can be proved.
The number of ordinary lines

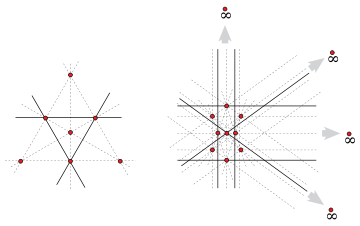
Let be the minimum number of ordinary lines determined over every set of n non-collinear points. Melchior's proof showed that raised the question of whether approaches infinity with n. confirmed this conjecture by proving that conjectured that for all values of n, a conjecture that still stands . This is often referred to as the Dirac-Motzkin conjecture, see for example . proved that t2(n) ≥ 3n/7.
Dirac's conjectured lower bound is asymptotically the best possible, since there is a proven matching upper bound for even n greater than four. The construction, due to Károly Böröczky, that achieves this bound consists of the vertices of a regular m-gon in the real projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
and another m points (thus) on the line at infinity corresponding to each of the directions determined by pairs of vertices; although there are pairs, they determine only m distinct directions. This arrangement has only m ordinary lines, namely those that connect a vertex v with the point at infinity corresponding to the line determined by vs two neighboring vertices. Note that, as with any finite configuration in the real projective plane, this construction can be perturbed so that all points are finite, without changing the number of ordinary lines.
For odd n, only two examples are known that match Dirac's lower bound conjecture, that is, with One example, by , consists of the vertices, edge midpoints, and centroid of an equilateral triangle; these seven points determine only three ordinary lines. The configuration in which these three ordinary lines are replaced by a single line cannot be realized in the Euclidean plane, but forms a finite projective space
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
known as the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
. The other counterexample, due to McKee, consists of two regular pentagons joined edge-to-edge together with the midpoint of the shared edge and four points on the line at infinity in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
; these 13 points have among them 6 ordinary lines.
, the best proven lower bound for t2(n) was obtained by who proved that except when n is seven. Asymptotically, this formula is already 12/13 ~ 92.3% of the proven n/2 upper bound. The n = 7 case is an exception because otherwise the Kelly–Moser construction would be a counterexample; their construction shows that t2(7) ≤ 3. However, were the Csima–Sawyer bound valid for n = 7, it would claim that t2(7) ≥ 4.
A closely related result is Beck's theorem
Beck's theorem (geometry)
In the context of discrete geometry, Beck's theorem may refer to several different results, two of which are given below. Both appeared, alongside several other important theorems, in a well-known paper by József Beck. The two results described below primarily concern lower bounds on the number of...
, stating a tradeoff between the number of lines with few points and the number of points on a single line.
See also
- Sylvester's theoremSylvester's theoremSylvester's theorem or Sylvester theorem may refer to any of several theorems named after James Joseph Sylvester:* The Sylvester–Gallai theorem, on the existence of a line with only two of n given points....
(disambiguation page) - List of topics named after James Joseph Sylvester
- The de Bruijn–Erdős theoremDe Bruijn–Erdős theorem (incidence geometry)In incidence geometry, the De Bruijn–Erdős theorem, originally published by Nicolaas Govert de Bruijn and Paul Erdős, states a lower bound on the number of lines determined by n points in a projective plane...
, a consequence of this theorem, states that a set of n noncollinear points determines n lines. - Orchard-planting problemOrchard-planting problemIn discrete geometry, the original orchard-planting problem asks for the maximum number of 3-point lines attainable by a configuration of points in the plane. Also called the Tree-planting problem, there are investigations into how many 4-, 5- & 6-point lines can be made...

