
Supersymmetry algebra
Encyclopedia
In theoretical physics
, a super-Poincaré algebra is an extension of the Poincaré algebra to incorporate supersymmetry
, a relation between boson
s and fermion
s. They are examples of supersymmetry algebra
s, and hence are Lie superalgebra
s. Thus a super-Poincaré algebra is a Z2 graded vector space with a graded Lie bracket such that the even part is a Lie algebra
containing the Poincaré algebra, and the odd part is built from spinor
s on which there is an anticommutation relation with values in the even part.
The simplest supersymmetric extension of the Poincaré algebra contains two Weyl spinors with the following anti-commutation relation: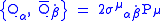
and all other anti-commutation relations between the Qs and Ps vanish. In the above expression are the generators of translation and
are the generators of translation and  are the Pauli matrices
are the Pauli matrices
.
To do this in full form it is easy to introduce the General Relativity metric. The Pauli and Dirac matrices should then depend on the metric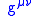 as:
as:

and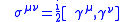
This then gives the full algebra
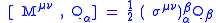

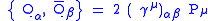
with the addition of the normal Poincaré algebra. It is a closed algebra since all Jacobi identities are satisfied and can have since explicit matrix representations. Following this line of reasoning will lead to Supergravity
.
states that the SUSY algebra with N spinor generators is as follows.
The even part of the star Lie superalgebra is the direct sum of the Poincaré algebra and a reductive Lie algebra B (such that its self-adjoint part is the tangent space of a real compact Lie group). The odd part of the algebra would be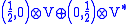
where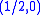 and
and 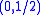 are specific representations of the Poincaré algebra. Both components are conjugate to each other under the * conjugation. V is an N-dimensional complex representation of B and V* is its dual representation
are specific representations of the Poincaré algebra. Both components are conjugate to each other under the * conjugation. V is an N-dimensional complex representation of B and V* is its dual representation
. The Lie bracket for the odd part is given by a symmetric equivariant
pairing {.,.} on the odd part with values in the even part. In particular, its reduced intertwiner from to the ideal
to the ideal
of the Poincaré algebra generated by translations is given as the product of a nonzero intertwiner from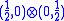 to (1/2,1/2). The "contraction intertwiner" from
to (1/2,1/2). The "contraction intertwiner" from 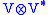 to the trivial representation
to the trivial representation
and the reduced intertwiner from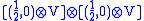 is the product of a (antisymmetric) intertwiner from (1/2,0) squared to (0,0) and an antisymmetric intertwiner A from
is the product of a (antisymmetric) intertwiner from (1/2,0) squared to (0,0) and an antisymmetric intertwiner A from 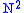 to B. * conjugate it to get the corresponding case for the other half.
to B. * conjugate it to get the corresponding case for the other half.
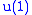 (called R-symmetry) and V is the 1D representation of
(called R-symmetry) and V is the 1D representation of 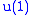 with "charge" 1. A (the intertwiner defined above) would have to be zero since it is antisymmetric.
with "charge" 1. A (the intertwiner defined above) would have to be zero since it is antisymmetric.
Actually, there are two versions of N=1 SUSY, one without the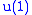 (i.e. B is zero dimensional) and the other with
(i.e. B is zero dimensional) and the other with 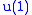 .
.
 and V is the 2D doublet representation of
and V is the 2D doublet representation of 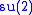 with a zero
with a zero 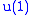 "charge". Now, A is a nonzero intertwiner to the
"charge". Now, A is a nonzero intertwiner to the 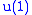 part of B.
part of B.
Alternatively, V could be a 2D doublet with a nonzero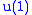 "charge". In this case, A would have to be zero.
"charge". In this case, A would have to be zero.
Yet another possibility would be to let B be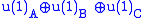 . V is invariant under
. V is invariant under 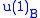 and
and 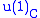 and decomposes into a 1D rep with
and decomposes into a 1D rep with  charge 1 and another 1D rep with charge -1. The intertwiner A would be complex with the real part mapping to
charge 1 and another 1D rep with charge -1. The intertwiner A would be complex with the real part mapping to 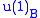 and the imaginary part mapping to
and the imaginary part mapping to 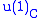 .
.
Or we could have B being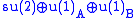 with V being the doublet rep of
with V being the doublet rep of 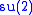 with zero
with zero 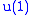 charges and A being a complex intertwiner with the real part mapping to
charges and A being a complex intertwiner with the real part mapping to  and the imaginary part to
and the imaginary part to 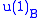 .
.
This doesn't even exhaust all the possibilities. We see that there is more than one N = 2 supersymmetry; likewise, the SUSYs for N > 2 are also not unique (in fact, it only gets worse).
that of an N=4 supersymmetric theory. So it is less often discussed compared to N=1,2,4 versions.
In 1 + 1, 5 + 1, 9 + 1 dimensions, etc., a SUSY algebra is classified by two nonnegative integers (M, N), at least one of which is nonzero. M represents the number of left-handed SUSYs and N represents the number of right-handed SUSYs.
The reason of this has to do with the reality conditions of the spinor
s.
Hereafter d = 9 means d = 8 + 1 in Minkowski signature, etc. The structure of supersymmetry algebra is mainly determined by the number of the fermionic generators, that is the number N times the real dimension of the spinor in d dimensions. It is because one can obtain a supersymmetry algebra of lower dimension easily from that of higher dimensionality by the use of dimensional reduction.
N = (1, 0) susy algebra with 16 supercharges is the minimal susy algebra in 10 dimensions.
It is also called the type I supersymmetry. Type IIA / IIB / I Superstring theory
has the susy algebra
of the corresponding name. The supersymmetry algebra for the heterotic superstrings is that of type I .
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, a super-Poincaré algebra is an extension of the Poincaré algebra to incorporate supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
, a relation between boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s. They are examples of supersymmetry algebra
Supersymmetry algebra
In theoretical physics, a super-Poincaré algebra is an extension of the Poincaré algebra to incorporate supersymmetry, a relation between bosons and fermions. They are examples of supersymmetry algebras, and hence are Lie superalgebras...
s, and hence are Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
s. Thus a super-Poincaré algebra is a Z2 graded vector space with a graded Lie bracket such that the even part is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
containing the Poincaré algebra, and the odd part is built from spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s on which there is an anticommutation relation with values in the even part.
The simplest supersymmetric extension of the Poincaré algebra contains two Weyl spinors with the following anti-commutation relation:
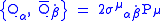
and all other anti-commutation relations between the Qs and Ps vanish. In the above expression
 are the generators of translation and
are the generators of translation and  are the Pauli matrices
are the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
.
To do this in full form it is easy to introduce the General Relativity metric. The Pauli and Dirac matrices should then depend on the metric
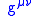 as:
as:
and
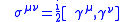
This then gives the full algebra
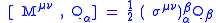

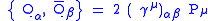
with the addition of the normal Poincaré algebra. It is a closed algebra since all Jacobi identities are satisfied and can have since explicit matrix representations. Following this line of reasoning will lead to Supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
.
SUSY in 3 + 1 Minkowski spacetime
In 3+1 Minkowski spacetime, the Haag-Lopuszanski-Sohnius theoremHaag-Lopuszanski-Sohnius theorem
In theoretical physics, the Haag–Lopuszanski–Sohnius theorem shows that the possible symmetries of a consistent 4-dimensional quantum field theory do not only consist of internal symmetries and Poincaré symmetry, but can also include supersymmetry as a nontrivial extension of the Poincaré algebra...
states that the SUSY algebra with N spinor generators is as follows.
The even part of the star Lie superalgebra is the direct sum of the Poincaré algebra and a reductive Lie algebra B (such that its self-adjoint part is the tangent space of a real compact Lie group). The odd part of the algebra would be
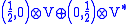
where
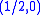 and
and 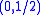 are specific representations of the Poincaré algebra. Both components are conjugate to each other under the * conjugation. V is an N-dimensional complex representation of B and V* is its dual representation
are specific representations of the Poincaré algebra. Both components are conjugate to each other under the * conjugation. V is an N-dimensional complex representation of B and V* is its dual representationDual representation
In mathematics, if G is a group and ρ is a linear representation of it on the vector space V, then the dual representation is defined over the dual vector space as follows:...
. The Lie bracket for the odd part is given by a symmetric equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
pairing {.,.} on the odd part with values in the even part. In particular, its reduced intertwiner from
 to the ideal
to the idealIdeal
-In philosophy:* Ideal , values that one actively pursues as goals* Platonic ideal, a philosophical idea of trueness of form, associated with Plato-In mathematics:* Ideal , special subsets of a ring considered in abstract algebra...
of the Poincaré algebra generated by translations is given as the product of a nonzero intertwiner from
 to (1/2,1/2). The "contraction intertwiner" from
to (1/2,1/2). The "contraction intertwiner" from 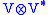 to the trivial representation
to the trivial representationTrivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
and the reduced intertwiner from
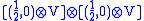 is the product of a (antisymmetric) intertwiner from (1/2,0) squared to (0,0) and an antisymmetric intertwiner A from
is the product of a (antisymmetric) intertwiner from (1/2,0) squared to (0,0) and an antisymmetric intertwiner A from 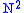 to B. * conjugate it to get the corresponding case for the other half.
to B. * conjugate it to get the corresponding case for the other half.N = 1
B is now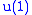 (called R-symmetry) and V is the 1D representation of
(called R-symmetry) and V is the 1D representation of 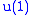 with "charge" 1. A (the intertwiner defined above) would have to be zero since it is antisymmetric.
with "charge" 1. A (the intertwiner defined above) would have to be zero since it is antisymmetric.Actually, there are two versions of N=1 SUSY, one without the
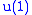 (i.e. B is zero dimensional) and the other with
(i.e. B is zero dimensional) and the other with 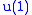 .
.N = 2
B is now and V is the 2D doublet representation of
and V is the 2D doublet representation of 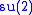 with a zero
with a zero 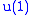 "charge". Now, A is a nonzero intertwiner to the
"charge". Now, A is a nonzero intertwiner to the 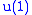 part of B.
part of B.Alternatively, V could be a 2D doublet with a nonzero
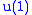 "charge". In this case, A would have to be zero.
"charge". In this case, A would have to be zero.Yet another possibility would be to let B be
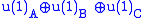 . V is invariant under
. V is invariant under 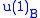 and
and 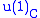 and decomposes into a 1D rep with
and decomposes into a 1D rep with  charge 1 and another 1D rep with charge -1. The intertwiner A would be complex with the real part mapping to
charge 1 and another 1D rep with charge -1. The intertwiner A would be complex with the real part mapping to 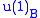 and the imaginary part mapping to
and the imaginary part mapping to 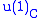 .
.Or we could have B being
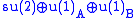 with V being the doublet rep of
with V being the doublet rep of 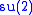 with zero
with zero 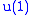 charges and A being a complex intertwiner with the real part mapping to
charges and A being a complex intertwiner with the real part mapping to  and the imaginary part to
and the imaginary part to 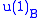 .
.This doesn't even exhaust all the possibilities. We see that there is more than one N = 2 supersymmetry; likewise, the SUSYs for N > 2 are also not unique (in fact, it only gets worse).
N = 3
It is theoretically allowed, but the multiplet structure becomes automatically the same withthat of an N=4 supersymmetric theory. So it is less often discussed compared to N=1,2,4 versions.
SUSY in various dimensions
In 0 + 1, 2 + 1, 3 + 1, 4 + 1, 6 + 1, 7 + 1, 8 + 1, 10 + 1 dimensions, etc., a SUSY algebra is classified by a positive integer N.In 1 + 1, 5 + 1, 9 + 1 dimensions, etc., a SUSY algebra is classified by two nonnegative integers (M, N), at least one of which is nonzero. M represents the number of left-handed SUSYs and N represents the number of right-handed SUSYs.
The reason of this has to do with the reality conditions of the spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s.
Hereafter d = 9 means d = 8 + 1 in Minkowski signature, etc. The structure of supersymmetry algebra is mainly determined by the number of the fermionic generators, that is the number N times the real dimension of the spinor in d dimensions. It is because one can obtain a supersymmetry algebra of lower dimension easily from that of higher dimensionality by the use of dimensional reduction.
d = 11
The only example is the N = 1 supersymmetry with 32 supercharges.d = 10
From d = 11, N = 1 susy, one obtains N = (1, 1) nonchiral susy algebra, which is also called the type IIA supersymmetry. There is also N = (2, 0) susy algebra, which is called the type IIB supersymmetry. Both of them have 32 supercharges.N = (1, 0) susy algebra with 16 supercharges is the minimal susy algebra in 10 dimensions.
It is also called the type I supersymmetry. Type IIA / IIB / I Superstring theory
Superstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
has the susy algebra
of the corresponding name. The supersymmetry algebra for the heterotic superstrings is that of type I .

