
Supersingular K3 surface
Encyclopedia
In algebraic geometry
, a supersingular K3 surface is a K3 surface
whose l-adic cohomology is generated by algebraic cycle
s; in other words, since the second Betti number
of a K3 surface is always 22, such a surface must possess 22 independent elements in its Picard group (ρ = 22).
Such surfaces can exist only in positive characteristic
, since in characteristic zero Hodge theory
gives an upper bound of 20 independent elements in the Picard group. In fact the Hodge diamond for any complex K3 surface is the same (see classification) and the middle row reads 1, 20, 1. In other words h2,0 and h0,2 both take the value 1, with h1,1 = 20. Therefore the dimension of the space spanned by the algebraic cycles is at most 20 in characteristic zero; surfaces with this maximum value are called singular K3 surfaces.
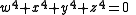
is a supersingular K3 surface over fields of characteristic 3 mod 4. Their theory was developed by and Tetsuji Shioda
.
Artin conjectured that every supersingular K3 surface is unirational; this conjecture remains open . has shown that supersingular K3 surfaces are double covers of the projective plane
. In the case of characteristic 2 the double cover may need to be an inseparable covering.
Artin's conjecture has been shown to be true in characteristic two by and more recently by Shimada.
The conjecture remains open in characteristic three; several families of examples have been constructed, showing that it is at least plausible.
The discriminant
of the intersection form
on the Picard group of a supersingular K3 surface is an even power
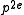
of the characteristic p, as was shown by Michael Artin and James S. Milne. Here e is defined to be the Artin invariant. We have
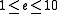
as was also shown by Michael Artin. There is a corresponding Artin stratification.
In characteristic two,
for a sufficiently general polynomial f(x, y) of degree six, defines a surface with twenty-one isolated singularities. It can be shown that the smooth projective minimal
model of the function field of such a surface is a supersingular K3 surface.
The largest Artin invariant here is ten.
Similarly, in characteristic three,
for a sufficiently general polynomial g(x, y) of degree four, defines a surface with nine isolated singularities. It can be shown that the smooth projective minimal
model of the function field of such a surface is again a supersingular K3 surface.
The highest Artin invariant in this family is six.
In characteristic five, demonstrated that every supersingular K3 surface with Artin invariant less than four is birationally equivalent to a surface with equation
and thus every such surface is unirational.
A by the mapping x → − x. More precisely, A should be a supersingular abelian surface, isogenous
to a product of two supersingular elliptic curves. showed that the Kummer surface is singular; the construction of S is as a minimal resolution
. made an extension to p = 2 with a group scheme
quotient.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a supersingular K3 surface is a K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
whose l-adic cohomology is generated by algebraic cycle
Algebraic cycle
In mathematics, an algebraic cycle on an algebraic variety V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology of V that is directly accessible in algebraic geometry...
s; in other words, since the second Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
of a K3 surface is always 22, such a surface must possess 22 independent elements in its Picard group (ρ = 22).
Such surfaces can exist only in positive characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
, since in characteristic zero Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
gives an upper bound of 20 independent elements in the Picard group. In fact the Hodge diamond for any complex K3 surface is the same (see classification) and the middle row reads 1, 20, 1. In other words h2,0 and h0,2 both take the value 1, with h1,1 = 20. Therefore the dimension of the space spanned by the algebraic cycles is at most 20 in characteristic zero; surfaces with this maximum value are called singular K3 surfaces.
History
The first example was given by , who observed that the Fermat quartic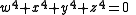
is a supersingular K3 surface over fields of characteristic 3 mod 4. Their theory was developed by and Tetsuji Shioda
Tetsuji Shioda
Tetsuji Shioda is a Japanese mathematician who introduced Shioda modular surfaces and who used Mordell–Weil lattices to give examples of dense sphere packings.-References:** in the Oberwolfach photo collection...
.
Artin conjectured that every supersingular K3 surface is unirational; this conjecture remains open . has shown that supersingular K3 surfaces are double covers of the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. In the case of characteristic 2 the double cover may need to be an inseparable covering.
Artin's conjecture has been shown to be true in characteristic two by and more recently by Shimada.
The conjecture remains open in characteristic three; several families of examples have been constructed, showing that it is at least plausible.
The discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of the intersection form
Intersection form
Intersection form may refer to:*Intersection theory *intersection form...
on the Picard group of a supersingular K3 surface is an even power
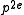
of the characteristic p, as was shown by Michael Artin and James S. Milne. Here e is defined to be the Artin invariant. We have
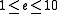
as was also shown by Michael Artin. There is a corresponding Artin stratification.
Examples
The elliptic modular surface of level 4 for characteristic 3 mod 4 is supersingular, as is the Kummer surface of a product of 2 supersingular elliptic curves in odd characteristic.In characteristic two,
- z2 = f(x, y) ,
for a sufficiently general polynomial f(x, y) of degree six, defines a surface with twenty-one isolated singularities. It can be shown that the smooth projective minimal
model of the function field of such a surface is a supersingular K3 surface.
The largest Artin invariant here is ten.
Similarly, in characteristic three,
- z3 = g(x, y) ,
for a sufficiently general polynomial g(x, y) of degree four, defines a surface with nine isolated singularities. It can be shown that the smooth projective minimal
model of the function field of such a surface is again a supersingular K3 surface.
The highest Artin invariant in this family is six.
In characteristic five, demonstrated that every supersingular K3 surface with Artin invariant less than four is birationally equivalent to a surface with equation
- z5 = h(x, y) ,
and thus every such surface is unirational.
Kummer surfaces
If the characteristic p is greater than 2, all supersingular K3 surfaces S with Artin invariant 0, 1 and 2 are birationally Kummer surfaces, in other words quotients of an abelian surfaceAbelian surface
In mathematics, an abelian surface is 2-dimensional abelian variety.One dimensional complex tori are just elliptic curves and are all algebraic, but Riemann discovered that most complex tori of dimension 2 are not algebraic...
A by the mapping x → − x. More precisely, A should be a supersingular abelian surface, isogenous
Isogeny
In mathematics, an isogeny is a morphism of varieties between two abelian varieties that is surjective and has a finite kernel....
to a product of two supersingular elliptic curves. showed that the Kummer surface is singular; the construction of S is as a minimal resolution
Resolution of singularities
In algebraic geometry, the problem of resolution of singularities asks whether every algebraic variety V has a resolution, a non-singular variety W with a proper birational map W→V...
. made an extension to p = 2 with a group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
quotient.

