
Stone duality
Encyclopedia
In mathematics
, there is an ample supply of categorical dualities between certain categories
of topological space
s and categories of partially ordered set
s. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation theorem for Boolean algebras
. These concepts are named in honor of Marshall Stone. Stone-type dualities also provide the foundation for pointless topology
and are exploited in theoretical computer science
for the study of formal semantics.
This article gives pointers to special cases of Stone duality and explains a very general instance thereof in detail.
s with continuous function
s and the category SFrm of spatial frames
with appropriate frame homomorphisms. The dual category
of SFrm is the category of locales
denoted by SLoc. The categorical equivalence
of Sob and SLoc is the basis for the mathematical area of pointless topology
, that is devoted to the study of Loc - the category of all locales of which SLoc is a full subcategory. The involved constructions are characteristic for this kind of duality, and are detailed below.
Now one can easily obtain a number of other dualities by restricting to certain special classes of sober spaces:
Many other Stone-type dualities could be added to these basic dualities.
s) which are spatial. This classical piece of mathematics requires a substantial amount of abstraction that usually tends to puzzle beginners. It should therefore be considered as graduate level mathematics. Some prior exposure to the basics of category theory
is recommended, although a deep understanding of the concepts of adjunction and duality may well arise from examples such as the result below. Furthermore, concepts of topology
and order theory
are naturally involved as well, where the later is probably more important for a thorough understanding.
s of elements from X, i.e. a subset of the powerset of X. It is known that Ω(X) has certain special properties: it is a complete lattice
within which suprema
and infima
of finite sets are given by set unions and finite set intersections, respectively. Furthermore, it contains both X and the empty set
. Since the embedding of Ω(X) into the powerset lattice of X preserves finite infima and arbitrary suprema, Ω(X) inherits the following distributivity law:
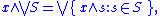
for every element (open set) x and every subset S of Ω(X). Hence Ω(X) is not an arbitrary complete lattice but a complete Heyting algebra (also called frame or locale - the various names are primarily used to distinguish several categories that have the same class of objects but different morphisms: frame morphisms, locale morphisms and homomorphisms of complete Heyting algebras). Now an obvious question is: To what extent is a topological space characterized by its locale of open sets?
As already hinted at above, one can go even further. The category Top of topological spaces has as morphisms the continuous functions, where a function f is continuous if the inverse image f −1(O) of any open set in the codomain
of f is open in the domain of f. Thus any continuous function f from a space X to a space Y defines an inverse mapping f −1 from Ω(Y) to Ω(X). Furthermore, it is easy to check that f −1 (like any inverse image map) preserves finite intersections and arbitrary unions and therefore is a morphism of frames. If we define Ω(f) = f −1 then Ω becomes a contravariant functor from the category Top to the category Frm of frames and frame morphisms. Using the tools of category theory, the task of finding a characterization of topological spaces in terms of their open set lattices is equivalent to finding a functor from Frm to Top which is adjoint
to Ω.
Let us first look at the points of a topological space X. One is usually tempted to consider a point of X as an element x of the set X, but there is in fact a more useful description for our current investigation. Any point x gives rise to a continuous function px from the one element topological space 1 (all subsets of which are open) to the space X by defining px(1) = x. Conversely, any function from 1 to X clearly determines one point: the element that it "points" to. Therefore the set of points of a topological space is equivalently characterized as the set of functions from 1 to X.
When using the functor Ω to pass from Top to Frm, all set-theoretic elements of a space are lost, but - using a fundamental idea of category theory - one can as well work on the function space
s. Indeed, any "point" px: 1 → X in Top is mapped to a morphism Ω(px): Ω(X) → Ω(1). The open set lattice of the one-element topological space Ω(1) is just (isomorphic to) the two-element locale 2 = { 0, 1 } with 0 < 1. After these observations it appears reasonable to define the set of points of a locale L to be the set of frame morphisms from L to 2. Yet, there is no guarantee that every point of the locale Ω(X) is in one-to-one correspondence to a point of the topological space X (consider again the indiscrete topology, for which the open set lattice has only one "point").
Before defining the required topology on pt(X), it is worthwhile to clarify the concept of a point of a locale further. The perspective motivated above suggests to consider a point of a locale L as a frame morphism p from L to 2. But these morphisms are characterized equivalently by the inverse images of the two elements of 2. From the properties of frame morphisms, one can derive that p −1(0) is a lower set (since p is monotone
), which contains a greatest element ap = V p −1(0) (since p preserves arbitrary suprema). In addition, the principal ideal
p −1(0) is a prime ideal
since p preserves finite infima and thus the principal ap is a meet-prime element. Now the set-inverse of p −1(0) given by p −1(1) is a completely prime filter
because p −1(0) is a principal prime ideal. It turns out that all of these descriptions uniquely determine the initial frame morphism. We sum up:
A point of a locale L is equivalently described as:
All of these descriptions have their place within the theory and it is convenient to switch between them as needed.
for every element a of L. Here we viewed the points of L as morphisms, but one can of course state a similar definition for all of the other equivalent characterizations. It can be shown that setting Ω(pt(L)) = {φ(a) | a ∈ L} does really yield a topological space (pt(L), Ω(pt(L))). It is common to abbreviate this space as pt(L).
Finally pt can be defined on morphisms of Frm rather canonically by defining, for a frame morphism g from L to M, pt(g): pt(M) → pt(L) as pt(g)(p) = p o g. In words, we obtain a morphism from L to 2 (a point of L) by applying the morphism g to get from L to M before applying the morphism p that maps from M to 2. Again, this can be formalized using the other descriptions of points of a locale as well - for example just calculate (p o g) −1(0).
to pt(Ω(X)) nor is L order-isomorphic
to Ω(pt(L)). However, when introducing the topology of pt(L) above, a mapping φ from L to Ω(pt(L)) was applied. This mapping is indeed a frame morphism. Conversely, we can define a continuous function ψ from X to pt(Ω(X)) by setting ψ(x) = Ω(px), where px is just the characteristic function for the point x from 1 to X as described above. Another convenient description is given by viewing points of a locale as meet-prime elements. In this case we have ψ(x) = X \ Cl{x}, where Cl{x} denotes the topological closure of the set {x} and \ is just set-difference.
At this point we already have more than enough data to obtain the desired result: the functors Ω and pt define an adjunction between the categories Top and Loc = Frmop, where pt is right adjoint to Ω and the natural transformation
s ψ and φop provide the required unit and counit, respectively.
For a space X, ψ: X → pt(Ω(X)) is a homeomorphism if and only if
it is bijective. Using the characterization via meet-prime elements of the open set lattice, one sees that this is the case if and only if every meet-prime open set is of the form X \ Cl{x} for a unique x. Alternatively, every join-prime closed set is the closure of a unique point, where "join-prime" can be replaced by (join-) irreducible since we are in a distributive lattice. Spaces with this property are called sober.
Conversely, for a locale L, φ: L → Ω(pt(L)) is always surjective. It is additionally injective if and only if any two elements a and b of L for which a is not less-or-equal to b can be separated by points of the locale, formally:
If this condition is satisfied for all elements of the locale, then the locale is spatial, or said to have enough points.
Finally, one can verify that for every space X, Ω(X) is spatial and for every locale L, pt(L) is sober. Hence, it follows that the above adjunction of Top and Loc restricts to an equivalence of the full subcategories Sob of sober spaces and SLoc of spatial locales. This main result is completed by the observation that for the functor pt o Ω, sending each space to the points of its open set lattice is right adjoint to the inclusion functor from Sob to Top. For a space X, pt(Ω(X)) is called its soberification. The case of the functor Ω o pt is symmetric but a special name for this operation is not commonly used.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, there is an ample supply of categorical dualities between certain categories
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and categories of partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation theorem for Boolean algebras
Stone's representation theorem for Boolean algebras
In mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
. These concepts are named in honor of Marshall Stone. Stone-type dualities also provide the foundation for pointless topology
Pointless topology
In mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
and are exploited in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
for the study of formal semantics.
This article gives pointers to special cases of Stone duality and explains a very general instance thereof in detail.
Overview of Stone-type dualities
Probably the most general duality which is classically referred to as "Stone duality" is the duality between the category Sob of sober spaceSober space
In mathematics, a sober space is a topological spacesuch that every irreducible closed subset of X is the closure of exactly one point of X: that is, has a unique generic point.-Properties and examples :...
s with continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s and the category SFrm of spatial frames
Complete Heyting algebra
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra which is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames...
with appropriate frame homomorphisms. The dual category
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of SFrm is the category of locales
Complete Heyting algebra
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra which is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames...
denoted by SLoc. The categorical equivalence
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
of Sob and SLoc is the basis for the mathematical area of pointless topology
Pointless topology
In mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
, that is devoted to the study of Loc - the category of all locales of which SLoc is a full subcategory. The involved constructions are characteristic for this kind of duality, and are detailed below.
Now one can easily obtain a number of other dualities by restricting to certain special classes of sober spaces:
- The category CohSp of coherentCoherent spaceIn proof theory, a coherent space is a concept introduced in the semantic study of linear logic.Let a set C be given. Two subsets S,T ⊆ C are said to be orthogonal, written S ⊥ T, if S ∩ T is ∅ or a singleton...
sober spaces (and coherent maps) is equivalent to the category CohLoc of coherent (or spectral) locales (and coherent maps), on the assumption of the Boolean prime ideal theoremBoolean prime ideal theoremIn mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
(in fact, this statement is equivalent to that assumption). The significance of this result stems from the fact that CohLoc in turn is dual to the category DLat of distributiveDistributivity (order theory)In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima...
latticesLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
. Hence, DLat is dual to CohSp - one obtains Stone's representation theorem for distributive lattices.
- When restricting further to coherent sober spaces which are HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, one obtains the category Stone of so-called Stone spaces. On the side of DLat, the restriction yields the subcategory Bool of Boolean algebras. Thus one obtains Stone's representation theorem for Boolean algebrasStone's representation theorem for Boolean algebrasIn mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
.
- Stone's representation for distributive lattices can be extended via an equivalence of coherent spaces and Priestley spacePriestley spaceIn mathematics, a Priestley space is an ordered topological space with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them. Priestley spaces play a fundamental role in the study of distributive lattices...
s (ordered topological spaces, that are compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and totally order-disconnected). One obtains a representation of distributive lattices via ordered topologies: Priestley's representation theorem for distributive lattices.
Many other Stone-type dualities could be added to these basic dualities.
Duality of sober spaces and spatial locales
This section motivates and explains one of the most basic constructions of Stone duality: the duality between topological spaces which are sober and frames (i.e. complete Heyting algebraComplete Heyting algebra
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra which is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames...
s) which are spatial. This classical piece of mathematics requires a substantial amount of abstraction that usually tends to puzzle beginners. It should therefore be considered as graduate level mathematics. Some prior exposure to the basics of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
is recommended, although a deep understanding of the concepts of adjunction and duality may well arise from examples such as the result below. Furthermore, concepts of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
are naturally involved as well, where the later is probably more important for a thorough understanding.
The lattice of open sets
The starting point for the theory is the fact that every topological space is characterized by a set of points X and a system Ω(X) of open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of elements from X, i.e. a subset of the powerset of X. It is known that Ω(X) has certain special properties: it is a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
within which suprema
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
and infima
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of finite sets are given by set unions and finite set intersections, respectively. Furthermore, it contains both X and the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. Since the embedding of Ω(X) into the powerset lattice of X preserves finite infima and arbitrary suprema, Ω(X) inherits the following distributivity law:
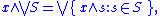
for every element (open set) x and every subset S of Ω(X). Hence Ω(X) is not an arbitrary complete lattice but a complete Heyting algebra (also called frame or locale - the various names are primarily used to distinguish several categories that have the same class of objects but different morphisms: frame morphisms, locale morphisms and homomorphisms of complete Heyting algebras). Now an obvious question is: To what extent is a topological space characterized by its locale of open sets?
As already hinted at above, one can go even further. The category Top of topological spaces has as morphisms the continuous functions, where a function f is continuous if the inverse image f −1(O) of any open set in the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
of f is open in the domain of f. Thus any continuous function f from a space X to a space Y defines an inverse mapping f −1 from Ω(Y) to Ω(X). Furthermore, it is easy to check that f −1 (like any inverse image map) preserves finite intersections and arbitrary unions and therefore is a morphism of frames. If we define Ω(f) = f −1 then Ω becomes a contravariant functor from the category Top to the category Frm of frames and frame morphisms. Using the tools of category theory, the task of finding a characterization of topological spaces in terms of their open set lattices is equivalent to finding a functor from Frm to Top which is adjoint
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
to Ω.
Points of a locale
The goal of this section is to define a functor pt from Frm to Top that in a certain sense "inverts" the operation of Ω by assigning to each locale L a set of points pt(L) (hence the notation pt) with a suitable topology. But how can we recover the set of points just from the locale, though it is not given as a lattice of sets? It is certain that one cannot expect in general that pt can reproduce all of the original elements of a topological space just from its lattice of open sets - for example all sets with the indiscrete topology yield (up to isomorphism) the same locale, such that the information on the specific set is no longer present. However, there is still a reasonable technique for obtaining "points" from a locale, which indeed gives an example of a central construction for Stone-type duality theorems.Let us first look at the points of a topological space X. One is usually tempted to consider a point of X as an element x of the set X, but there is in fact a more useful description for our current investigation. Any point x gives rise to a continuous function px from the one element topological space 1 (all subsets of which are open) to the space X by defining px(1) = x. Conversely, any function from 1 to X clearly determines one point: the element that it "points" to. Therefore the set of points of a topological space is equivalently characterized as the set of functions from 1 to X.
When using the functor Ω to pass from Top to Frm, all set-theoretic elements of a space are lost, but - using a fundamental idea of category theory - one can as well work on the function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s. Indeed, any "point" px: 1 → X in Top is mapped to a morphism Ω(px): Ω(X) → Ω(1). The open set lattice of the one-element topological space Ω(1) is just (isomorphic to) the two-element locale 2 = { 0, 1 } with 0 < 1. After these observations it appears reasonable to define the set of points of a locale L to be the set of frame morphisms from L to 2. Yet, there is no guarantee that every point of the locale Ω(X) is in one-to-one correspondence to a point of the topological space X (consider again the indiscrete topology, for which the open set lattice has only one "point").
Before defining the required topology on pt(X), it is worthwhile to clarify the concept of a point of a locale further. The perspective motivated above suggests to consider a point of a locale L as a frame morphism p from L to 2. But these morphisms are characterized equivalently by the inverse images of the two elements of 2. From the properties of frame morphisms, one can derive that p −1(0) is a lower set (since p is monotone
Monotone
Monotone refers to a sound, for example speech or music, that has a single unvaried tone.Monotone or monotonicity may also refer to:*Monotone , an open source revision control system*Monotone class theorem, in measure theory...
), which contains a greatest element ap = V p −1(0) (since p preserves arbitrary suprema). In addition, the principal ideal
Ideal (order theory)
In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
p −1(0) is a prime ideal
Ideal (order theory)
In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
since p preserves finite infima and thus the principal ap is a meet-prime element. Now the set-inverse of p −1(0) given by p −1(1) is a completely prime filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
because p −1(0) is a principal prime ideal. It turns out that all of these descriptions uniquely determine the initial frame morphism. We sum up:
A point of a locale L is equivalently described as:
- a frame morphism from L to 2
- a principal prime ideal of L
- a meet-prime element of L
- a completely prime filter of L.
All of these descriptions have their place within the theory and it is convenient to switch between them as needed.
The functor pt
Now that a set of points is available for any locale, it remains to equip this set with an appropriate topology in order to define the object part of the functor pt. This is done by defining the open sets of pt(L) as- φ(a) = { p ∈ pt(L) | p(a) = 1 },
for every element a of L. Here we viewed the points of L as morphisms, but one can of course state a similar definition for all of the other equivalent characterizations. It can be shown that setting Ω(pt(L)) = {φ(a) | a ∈ L} does really yield a topological space (pt(L), Ω(pt(L))). It is common to abbreviate this space as pt(L).
Finally pt can be defined on morphisms of Frm rather canonically by defining, for a frame morphism g from L to M, pt(g): pt(M) → pt(L) as pt(g)(p) = p o g. In words, we obtain a morphism from L to 2 (a point of L) by applying the morphism g to get from L to M before applying the morphism p that maps from M to 2. Again, this can be formalized using the other descriptions of points of a locale as well - for example just calculate (p o g) −1(0).
The adjunction of Top and Loc
As noted several times before, pt and Ω usually are not inverses. In general neither is X homeomorphicHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to pt(Ω(X)) nor is L order-isomorphic
Order isomorphism
In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...
to Ω(pt(L)). However, when introducing the topology of pt(L) above, a mapping φ from L to Ω(pt(L)) was applied. This mapping is indeed a frame morphism. Conversely, we can define a continuous function ψ from X to pt(Ω(X)) by setting ψ(x) = Ω(px), where px is just the characteristic function for the point x from 1 to X as described above. Another convenient description is given by viewing points of a locale as meet-prime elements. In this case we have ψ(x) = X \ Cl{x}, where Cl{x} denotes the topological closure of the set {x} and \ is just set-difference.
At this point we already have more than enough data to obtain the desired result: the functors Ω and pt define an adjunction between the categories Top and Loc = Frmop, where pt is right adjoint to Ω and the natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s ψ and φop provide the required unit and counit, respectively.
The duality theorem
The above adjunction is not an equivalence of the categories Top and Loc (or, equivalently, a duality of Top and Frm). For this it is necessary that both ψ and φ are isomorphisms in their respective categories.For a space X, ψ: X → pt(Ω(X)) is a homeomorphism if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is bijective. Using the characterization via meet-prime elements of the open set lattice, one sees that this is the case if and only if every meet-prime open set is of the form X \ Cl{x} for a unique x. Alternatively, every join-prime closed set is the closure of a unique point, where "join-prime" can be replaced by (join-) irreducible since we are in a distributive lattice. Spaces with this property are called sober.
Conversely, for a locale L, φ: L → Ω(pt(L)) is always surjective. It is additionally injective if and only if any two elements a and b of L for which a is not less-or-equal to b can be separated by points of the locale, formally:
- if not a ≤ b, then there is a point p in pt(L) such that p(a) = 1 and p(b) = 0.
If this condition is satisfied for all elements of the locale, then the locale is spatial, or said to have enough points.
Finally, one can verify that for every space X, Ω(X) is spatial and for every locale L, pt(L) is sober. Hence, it follows that the above adjunction of Top and Loc restricts to an equivalence of the full subcategories Sob of sober spaces and SLoc of spatial locales. This main result is completed by the observation that for the functor pt o Ω, sending each space to the points of its open set lattice is right adjoint to the inclusion functor from Sob to Top. For a space X, pt(Ω(X)) is called its soberification. The case of the functor Ω o pt is symmetric but a special name for this operation is not commonly used.

