
Ideal (order theory)
Encyclopedia
In mathematical
order theory
, an ideal is a special subset of a partially ordered set
(poset). Although this term historically was derived from the notion of a ring ideal of abstract algebra
, it has subsequently been generalized to a different notion. Ideals are of great importance for many constructions in order and lattice theory.
While this is the most general way to define an ideal for arbitrary posets, it was originally defined for lattice
s only. In this case, the following equivalent definition can be given:
a subset I of a lattice (P,≤) is an ideal if and only if
it is a lower set that is closed under finite joins (suprema), i.e., it is nonempty and for all x, y in I, the element x y of P is also in I.
y of P is also in I.
The dual
notion of an ideal, i.e. the concept obtained by reversing all ≤ and exchanging with
with  , is a filter
, is a filter
. The terms order ideal, order filter, semi-ideal, down-set and decreasing subset are sometimes used for arbitrary lower or upper sets. Wikipedia uses only "ideal/filter (of order theory)" and "lower/upper set" to avoid confusion.
Frink ideal
s, pseudoideal
s and Doyle pseudoideals
are different generalizations of the notion of a lattice ideal.
An ideal or filter is said to be proper if it is not equal to the whole set P.
The smallest ideal that contains a given element p is a principal ideal and p is said to be a principal element of the ideal in this situation. The principal ideal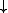 p for a principal p is thus given by
p for a principal p is thus given by 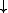 p = {x in P | x ≤ p}.
p = {x in P | x ≤ p}.
A subset I of a lattice (P,≤) is a prime ideal, if and only if
It is easily checked that this indeed is equivalent to stating that P\I is a filter (which is then also prime, in the dual sense).
For a complete lattice
the further notion of a completely prime ideal
is meaningful. It is defined to be a proper ideal I with the additional
property that, whenever the meet (infimum
) of some arbitrary set A
is in I, some element of A is also in I. So this is just a
specific prime ideal that extends the above conditions to infinite meets.
The existence of prime ideals is in general not obvious, and often a satisfactory amount of prime ideals cannot be derived within Zermelo–Fraenkel set theory
. This issue is discussed in various prime ideal theorem
s, which are necessary for many applications that require prime ideals.
When a poset is a distributive lattice
, maximal ideals and filters are necessarily prime, while the converse of this statement is false in general.
Maximal filters are sometimes called ultrafilter
s, but this terminology is often reserved for Boolean algebras, where a maximal filter (ideal) is a filter (ideal) that contains exactly one of the elements {a, ¬a}, for each element a of the Boolean algebra. In Boolean algebras, the terms prime ideal and maximal ideal coincide, as do the terms prime filter and maximal filter.
There is another interesting notion of maximality of ideals: Consider an ideal I and a filter F such that I is disjoint from F. We are interested in an ideal M which is maximal among all ideals that contain I and are disjoint from F. In the case of distributive lattices such an M is always a prime ideal. A proof of this statement follows.
However, in general it is not clear whether there exists any ideal M that is maximal in this sense. Yet, if we assume the Axiom of Choice in our set theory, then the existence of M for every disjoint filter–ideal-pair can be shown. In the special case that the considered order is a Boolean algebra, this theorem is called the Boolean prime ideal theorem
. It is strictly weaker than the Axiom of Choice and it turns out that nothing more is needed for many order theoretic applications of ideals.
of Boolean algebras and of Boolean ring
s, both notions do indeed coincide.
and lattice theory, and the literature on the Boolean prime ideal theorem
.
A monograph available free online:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, an ideal is a special subset of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(poset). Although this term historically was derived from the notion of a ring ideal of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, it has subsequently been generalized to a different notion. Ideals are of great importance for many constructions in order and lattice theory.
Basic definitions
A non-empty subset I of a partially ordered set (P,≤) is an ideal, if the following conditions hold:- For every x in I, y ≤ x implies that y is in I. (I is a lower set)
- For every x, y in I, there is some element z in I, such that x ≤ z and y ≤ z. (I is a directed setDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
)
While this is the most general way to define an ideal for arbitrary posets, it was originally defined for lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
s only. In this case, the following equivalent definition can be given:
a subset I of a lattice (P,≤) is an ideal if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is a lower set that is closed under finite joins (suprema), i.e., it is nonempty and for all x, y in I, the element x
 y of P is also in I.
y of P is also in I.The dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
notion of an ideal, i.e. the concept obtained by reversing all ≤ and exchanging
 with
with  , is a filter
, is a filterFilter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
. The terms order ideal, order filter, semi-ideal, down-set and decreasing subset are sometimes used for arbitrary lower or upper sets. Wikipedia uses only "ideal/filter (of order theory)" and "lower/upper set" to avoid confusion.
Frink ideal
Frink ideal
In mathematics, a Frink ideal, introduced by Orrin Frink, is a certain kind of subset of a partially ordered set.- Basic definitions :LU is the set of all lower bounds of the set of all upper bounds of the subset A of a partially ordered set....
s, pseudoideal
Pseudoideal
- Basic definitions :LU is the set of all lower bounds of the set of all upper bounds of the subset A of a partially ordered set.A subset I of a partially ordered set is a Doyle pseudoideal, if the following condition holds:...
s and Doyle pseudoideals
Pseudoideal
- Basic definitions :LU is the set of all lower bounds of the set of all upper bounds of the subset A of a partially ordered set.A subset I of a partially ordered set is a Doyle pseudoideal, if the following condition holds:...
are different generalizations of the notion of a lattice ideal.
An ideal or filter is said to be proper if it is not equal to the whole set P.
The smallest ideal that contains a given element p is a principal ideal and p is said to be a principal element of the ideal in this situation. The principal ideal
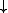 p for a principal p is thus given by
p for a principal p is thus given by 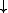 p = {x in P | x ≤ p}.
p = {x in P | x ≤ p}.Prime ideals
An important special case of an ideal is constituted by those ideals whose set-theoretic complements are filters, i.e. ideals in the inverse order. Such ideals are called prime ideals. Also note that, since we require ideals and filters to be non-empty, every prime filter is necessarily proper. For lattices, prime ideals can be characterized as follows:A subset I of a lattice (P,≤) is a prime ideal, if and only if
- I is an ideal of P, and
- for every elements x and y of P, x
 y in I implies that x is in I or y is in I.
y in I implies that x is in I or y is in I.
It is easily checked that this indeed is equivalent to stating that P\I is a filter (which is then also prime, in the dual sense).
For a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
the further notion of a completely prime ideal
is meaningful. It is defined to be a proper ideal I with the additional
property that, whenever the meet (infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
) of some arbitrary set A
is in I, some element of A is also in I. So this is just a
specific prime ideal that extends the above conditions to infinite meets.
The existence of prime ideals is in general not obvious, and often a satisfactory amount of prime ideals cannot be derived within Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
. This issue is discussed in various prime ideal theorem
Prime ideal theorem
In mathematics, the prime ideal theorem may be* the Boolean prime ideal theorem* the Landau prime ideal theorem on number fields...
s, which are necessary for many applications that require prime ideals.
Maximal ideals
An ideal I is maximal if it is proper and there is no proper ideal J which is a strictly greater set than I. Likewise, a filter F is maximal if it is proper and there is no proper filter which is strictly greater.When a poset is a distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
, maximal ideals and filters are necessarily prime, while the converse of this statement is false in general.
Maximal filters are sometimes called ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s, but this terminology is often reserved for Boolean algebras, where a maximal filter (ideal) is a filter (ideal) that contains exactly one of the elements {a, ¬a}, for each element a of the Boolean algebra. In Boolean algebras, the terms prime ideal and maximal ideal coincide, as do the terms prime filter and maximal filter.
There is another interesting notion of maximality of ideals: Consider an ideal I and a filter F such that I is disjoint from F. We are interested in an ideal M which is maximal among all ideals that contain I and are disjoint from F. In the case of distributive lattices such an M is always a prime ideal. A proof of this statement follows.
-
- Proof. Assume the ideal M is maximal with respect to disjointness from the filter F. Suppose for a contradiction that M is not prime, i.e. there exists a pair of elements a and b such that a
 b in M but neither a nor b are in M. Consider the case that for all m in M, m
b in M but neither a nor b are in M. Consider the case that for all m in M, m a is not in F. One can construct an ideal N by taking the downward closure of the set of all binary joins of this form, i.e. N = { x | x≤ m
a is not in F. One can construct an ideal N by taking the downward closure of the set of all binary joins of this form, i.e. N = { x | x≤ m a for some m in M}. It is readily checked that N is indeed an ideal disjoint from F which is strictly greater than M. But this contradicts the maximality of M and thus the assumption that M is not prime.
a for some m in M}. It is readily checked that N is indeed an ideal disjoint from F which is strictly greater than M. But this contradicts the maximality of M and thus the assumption that M is not prime. - For the other case, assume that there is some m in M with m
 a in F. Now if any element n in M is such that n
a in F. Now if any element n in M is such that n b is in F, one finds that (m
b is in F, one finds that (m n)
n) b and (m
b and (m n)
n) a are both in F. But then their meet is in F and, by distributivity, (m
a are both in F. But then their meet is in F and, by distributivity, (m n)
n)  (a
(a b) is in F too. On the other hand, this finite join of elements of M is clearly in M, such that the assumed existence of n contradicts the disjointness of the two sets. Hence all elements n of M have a join with b that is not in F. Consequently one can apply the above construction with b in place of a to obtain an ideal that is strictly greater than M while being disjoint from F. This finishes the proof.
b) is in F too. On the other hand, this finite join of elements of M is clearly in M, such that the assumed existence of n contradicts the disjointness of the two sets. Hence all elements n of M have a join with b that is not in F. Consequently one can apply the above construction with b in place of a to obtain an ideal that is strictly greater than M while being disjoint from F. This finishes the proof.
- Proof. Assume the ideal M is maximal with respect to disjointness from the filter F. Suppose for a contradiction that M is not prime, i.e. there exists a pair of elements a and b such that a
However, in general it is not clear whether there exists any ideal M that is maximal in this sense. Yet, if we assume the Axiom of Choice in our set theory, then the existence of M for every disjoint filter–ideal-pair can be shown. In the special case that the considered order is a Boolean algebra, this theorem is called the Boolean prime ideal theorem
Boolean prime ideal theorem
In mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
. It is strictly weaker than the Axiom of Choice and it turns out that nothing more is needed for many order theoretic applications of ideals.
Applications
The construction of ideals and filters is an important tool in many applications of order theory.- In Stone's representation theorem for Boolean algebrasStone's representation theorem for Boolean algebrasIn mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
, the maximal ideals (or, equivalently via the negation map, ultrafilters) are used to obtain the set of points of a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, whose clopen setClopen setIn topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
s are isomorphicIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the original Boolean algebra.
- Order theory knows many completion procedures, to turn posets into posets with additional completenessCompleteness (order theory)In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
properties. For example, the ideal completion of a given partial order P is the set of all ideals of P ordered by subset inclusion. This construction yields the freeFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
dcpo generated by P. Furthermore the ideal completion serves to reconstruct any algebraic dcpo from its set of compact elementCompact elementIn the mathematical area of order theory, the compact or finite elements of a partially ordered set are those elements that cannot be subsumed by a supremum of any non-empty directed set that does not already contain members above the compact element....
s.
History
Ideals were introduced first by Marshall H. Stone, who derived their name from the ring ideals of abstract algebra. He adopted this terminology because, using the isomorphism of the categoriesIsomorphism of categories
In category theory, two categories C and D are isomorphic if there exist functors F : C → D and G : D → C which are mutually inverse to each other, i.e. FG = 1D and GF = 1C. This means that both the objects and the morphisms of C and D stand in a one to one correspondence to each other...
of Boolean algebras and of Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
s, both notions do indeed coincide.
Literature
Ideals and filters are among the most basic concepts of order theory. See the introductory books given for order theoryOrder theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
and lattice theory, and the literature on the Boolean prime ideal theorem
Boolean prime ideal theorem
In mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
.
A monograph available free online:
- Burris, Stanley N.; and Sankappanavar, Hanamantagouda P.; 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.

