Stinespring factorization theorem
Encyclopedia
In mathematics
, Stinespring's dilation theorem, also called Stinespring's factorization theorem, named after W. Forrest Stinespring, is a result from operator theory
that represents any completely positive map
on a C*-algebra as a composition of two completely positive maps each of which has a special form:
Theorem. Let A be a unital C*-algebra, H be a Hilbert space, and B(H) be the bounded operators on H. For every completely positive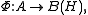
there exists a Hilbert space K and a unital *-homomorphism
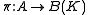
such that
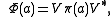
where
is a bounded operator. Furthermore, we have
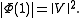
Informally, one can say that every completely positive map Φ can be "lifted" up to a map of the form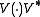
.
The converse of the theorem is true trivially. So Stinespring's result classifies completely positive maps.
.
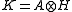For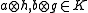
, define
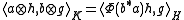
and extend by linearity to all of K. We see that this is a bilinear form by definition. By the completely positivity of Φ, it is also positive. The assumption that Φ preserves positivity means Φ commutes with the * operation in A, which can be used to show that
is conjugate-symmetric. Therefore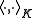 
is a, possibly degenerate, Hermitian bilinear form. Since Hermitian bilinear forms satisfy the Cauchy Schwarz inequality, the subset
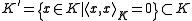
is a subspace. We can remove degeneracy by considering the quotient space
K / K' . The completion of this quotient space is then a Hilbert space, also denoted by K. Next define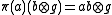
and 
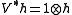, where 1 is the unit in A. One can check that π and V have the desired properties.
Notice that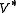
is just the natural algebraic embedding of H into K. Direct calculation shows that, in the finite dimensional case, 
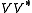can be identified with the algebraic identity map on H. The definitions of 
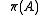and K are also rather natural. Thus the key element of the proof is the introduction of 
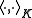. In particular, after the algebraic embedding, H is "re-normed" in the following sense: If h is identified with 
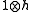, then
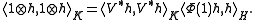
This can be viewed as the restriction of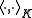
to H.
When Φ is unital, i.e.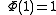
, we see that 
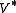is an isometry and H can be embedded, in the Hilbert space sense, into K. V, acting on K, becomes the projection onto H. Symbolically, we can write
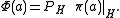
In the language of dilation theory, this is to say that Φ(a) is a compression of π(a). It is therefore a corollary of Stinespring's theorem that every unital completely positive map is the compression of some *-homomorphism.
Let K1 be the closed linear span of π(A) V*H. By property of *-representations in general, K1 is an invariant subspace of π(a) for all a. Also, K1 contains V*H. Define
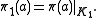
We can compute directly
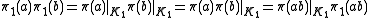
and if k and l lie in K1
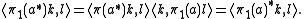
So (π1, V, K1) is also a Stinespring representation of Φ and has the additional property that K1 is the closed linear span of π(A) V*H. Such a representation is called a minimal Stinespring representation.
W : K1 → K2 by
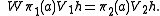
On V1H ⊂ K1, this gives the interwining relation
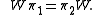
In particular, when both Stinespring representations are minimal, W is unitary. Thus minimal Stinespring representations are unique up to a unitary transformation.
, that is, Φ has norm 1, then the isometry
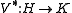is determined by
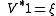
for some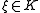
of unit norm. So
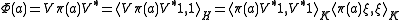
and we have recovered the GNS representation of states.
This is one way to see that completely positive maps, rather than merely positive ones, are the true generalizations of positive functionals.
A linear positive functional on a C*-algebra is absolutely continuous with respect to another such (called reference) functional if it is zero on any positive element on which the reference positive functional is zero. This leads to a noncommutative generalization of Radon-Nikodym theorem. The usual density operator of states on the matrix algebras with respect to the standard trace is nothing but the Radon-Nikodym derivative when the reference functional is chosen to be trace. Belavkin
introduced the notion of complete absolute continuity of one completely positive map with respect to another (reference) map and proved an operator variant of the noncommutative Radon-Nikodym theorem for completely positive maps. A particular case of this theorem corresponding to a tracial completely positive reference map on the matrix algebras leads to the Choi operator as a Radon-Nikodym derivative of a CP map with respect to the standard trace (see Choi's Theorem).
Choi's theorem
It was shown by Choi that if 
is completely positive, where G and H are finite dimensional Hilbert spaces of dimensions n and m respectively, then Φ takes the form:
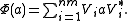
Choi proved this using linear algebra techniques, but his result can also be viewed as a special case of Stinespring's theorem: Let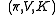
be a minimal Stinespring representation of Φ. By minimality, K has dimension less than that of 
. So without loss of generality, K can be identified with
.
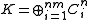Each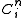
is a copy of the n-dimensional Hilbert space. From 
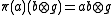, we see that the above identification of K can be arranged so 
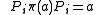, where 
is the projection from K to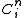 
. Let 
. We have
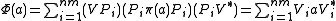
and Choi's result is proved.
Choi's result is a particular case of noncommutative Radon-Nikodym theorem for completely positive (CP) maps corresponding to a tracial completely positive reference map on the matrix algebras. In strong operator form this general theorem was proven by Belavkin in 1985 who showed the existence of the positive density operator representing a CP map which is completely absolutely continuous with respect to a reference CP map. The uniqueness of this density operator in the reference Steinspring representation simply follows from the minimality of this representation. Thus, Choi's operator is the Radon-Nikodym derivative of a finite-dimensional CP map with respect to the standard trace.
Notice that, in proving Choi's theorem, as well as Belavkin's theorem from Stinespring's formulation, the argument does not give the Kraus operators Vi explicitly, unless one makes the various identification of spaces explicit. On the other hand, Choi's original proof involves direct calculation of those operators.
Naimark's dilation theorem
Naimark's theorem says that every B(H)-valued, weakly countably-additive measure on some compact Hausdorff space X can be "lifted" so that the measure becomes a spectral measure. It can be proved by combining the fact that C(X) is a commutative C*-algebra and Stinespring's theorem.
Sz.-Nagy's dilation theorem
This result states that every contraction on a Hilbert space has a unitary dilation
with the minimality property.
s, or quantum operation
s, are defined to be completely positive maps between C*-algebras. Being a classification for all such maps, Stinespring's theorem is important in that context. For example, the uniqueness part of the theorem has been used to classify certain classes of quantum channels.
For the comparison of different channels and computation of their mutual fidelities and information another representation of the channels by their "Radon-Nikodym" derivatives introduced by Belavkin is useful. In the finite dimensional case, Choi's theorem as the tracial variant of the Belavkin's Radon-Nikodym theorem for completely positive maps is also relevant. The operators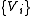
from the expression
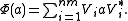
are called the Kraus operators of Φ. The expression
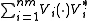
is sometimes called the operator sum representation of Φ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Stinespring's dilation theorem, also called Stinespring's factorization theorem, named after W. Forrest Stinespring, is a result from operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
that represents any completely positive map
Choi's theorem on completely positive maps
In mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
on a C*-algebra as a composition of two completely positive maps each of which has a special form:
- A *-representation of A on some auxiliary Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
K followed by - An operator map of the form T → V T V*.
Formulation
In the case of a unital C*-algebra, the result is as follows:Theorem. Let A be a unital C*-algebra, H be a Hilbert space, and B(H) be the bounded operators on H. For every completely positive
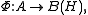
there exists a Hilbert space K and a unital *-homomorphism
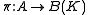
such that
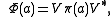
where
is a bounded operator. Furthermore, we have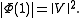Informally, one can say that every completely positive map Φ can be "lifted" up to a map of the form
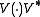.The converse of the theorem is true trivially. So Stinespring's result classifies completely positive maps.
Sketch of proof
We now briefly sketch the proof. Let.For
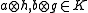, define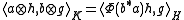and extend by linearity to all of K. We see that this is a bilinear form by definition. By the completely positivity of Φ, it is also positive. The assumption that Φ preserves positivity means Φ commutes with the * operation in A, which can be used to show that
is conjugate-symmetric. Therefore 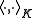is a, possibly degenerate, Hermitian bilinear form. Since Hermitian bilinear forms satisfy the Cauchy Schwarz inequality, the subset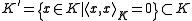is a subspace. We can remove degeneracy by considering the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
K / K' . The completion of this quotient space is then a Hilbert space, also denoted by K. Next define
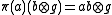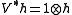and , where 1 is the unit in A. One can check that π and V have the desired properties.Notice that
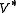is just the natural algebraic embedding of H into K. Direct calculation shows that, in the finite dimensional case, 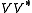can be identified with the algebraic identity map on H. The definitions of 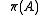and K are also rather natural. Thus the key element of the proof is the introduction of 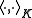. In particular, after the algebraic embedding, H is "re-normed" in the following sense: If h is identified with 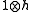, then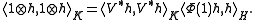This can be viewed as the restriction of
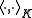to H.When Φ is unital, i.e.
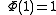, we see that 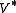is an isometry and H can be embedded, in the Hilbert space sense, into K. V, acting on K, becomes the projection onto H. Symbolically, we can write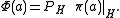In the language of dilation theory, this is to say that Φ(a) is a compression of π(a). It is therefore a corollary of Stinespring's theorem that every unital completely positive map is the compression of some *-homomorphism.
Minimality
The triple (π, V, K) is called a Stinespring representation of Φ. A natural question is now whether one can reduce a given Stinespring representation in some sense.Let K1 be the closed linear span of π(A) V*H. By property of *-representations in general, K1 is an invariant subspace of π(a) for all a. Also, K1 contains V*H. Define
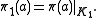
We can compute directly
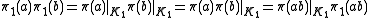
and if k and l lie in K1
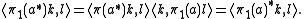
So (π1, V, K1) is also a Stinespring representation of Φ and has the additional property that K1 is the closed linear span of π(A) V*H. Such a representation is called a minimal Stinespring representation.
Uniqueness
Let (π1, V1, K1) and (π2, V2, K2) be two Stinespring representations of a given Φ. Define a partial isometryPartial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
W : K1 → K2 by
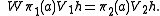
On V1H ⊂ K1, this gives the interwining relation
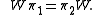
In particular, when both Stinespring representations are minimal, W is unitary. Thus minimal Stinespring representations are unique up to a unitary transformation.
Some consequences
We mention a few of the results which can be viewed as consequences of Stinespring's theorem. Historically, some of the results below preceded Stinespring's theorem.GNS construction
Let H in Stinespring's theorem be 1-dimensional, i.e. the complex numbers. So Φ now is a positive linear functional on A. If we assume Φ is a stateState (functional analysis)
In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
, that is, Φ has norm 1, then the isometry
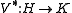is determined by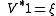for some
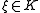of unit norm. So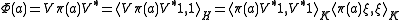and we have recovered the GNS representation of states.
This is one way to see that completely positive maps, rather than merely positive ones, are the true generalizations of positive functionals.
A linear positive functional on a C*-algebra is absolutely continuous with respect to another such (called reference) functional if it is zero on any positive element on which the reference positive functional is zero. This leads to a noncommutative generalization of Radon-Nikodym theorem. The usual density operator of states on the matrix algebras with respect to the standard trace is nothing but the Radon-Nikodym derivative when the reference functional is chosen to be trace. Belavkin
Viacheslav Belavkin
Viacheslav Pavlovich Belavkin is a professor in applied mathematics at the University of Nottingham. He was born in Lwów, and graduated from Moscow State University in 1970. In 1996, he and Ruslan L. Stratonovich were awarded the Main State Prize of the Russian Federation for outstanding...
introduced the notion of complete absolute continuity of one completely positive map with respect to another (reference) map and proved an operator variant of the noncommutative Radon-Nikodym theorem for completely positive maps. A particular case of this theorem corresponding to a tracial completely positive reference map on the matrix algebras leads to the Choi operator as a Radon-Nikodym derivative of a CP map with respect to the standard trace (see Choi's Theorem).
Choi's theoremChoi's theorem on completely positive mapsIn mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
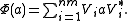
It was shown by Choi that if is completely positive, where G and H are finite dimensional Hilbert spaces of dimensions n and m respectively, then Φ takes the form:Choi proved this using linear algebra techniques, but his result can also be viewed as a special case of Stinespring's theorem: Let
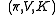be a minimal Stinespring representation of Φ. By minimality, K has dimension less than that of . So without loss of generality, K can be identified with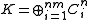.Each
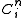is a copy of the n-dimensional Hilbert space. From 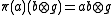, we see that the above identification of K can be arranged so 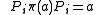, where is the projection from K to 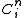. Let . We have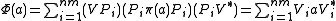and Choi's result is proved.
Choi's result is a particular case of noncommutative Radon-Nikodym theorem for completely positive (CP) maps corresponding to a tracial completely positive reference map on the matrix algebras. In strong operator form this general theorem was proven by Belavkin in 1985 who showed the existence of the positive density operator representing a CP map which is completely absolutely continuous with respect to a reference CP map. The uniqueness of this density operator in the reference Steinspring representation simply follows from the minimality of this representation. Thus, Choi's operator is the Radon-Nikodym derivative of a finite-dimensional CP map with respect to the standard trace.
Notice that, in proving Choi's theorem, as well as Belavkin's theorem from Stinespring's formulation, the argument does not give the Kraus operators Vi explicitly, unless one makes the various identification of spaces explicit. On the other hand, Choi's original proof involves direct calculation of those operators.
Naimark's dilation theoremNaimark's dilation theoremIn operator theory, Naimark's dilation theorem is a result that characterizes positive operator valued measures. It can be viewed as a consequence of Stinespring's dilation theorem.- Note :...
Naimark's theorem says that every B(H)-valued, weakly countably-additive measure on some compact Hausdorff space X can be "lifted" so that the measure becomes a spectral measure. It can be proved by combining the fact that C(X) is a commutative C*-algebra and Stinespring's theorem. Sz.-Nagy's dilation theoremSz.-Nagy's dilation theoremThe Sz.-Nagy dilation theorem states that every contraction T on a Hilbert space H has a unitary dilation U to a Hilbert space K, containing H, withT^n = P_H U^n \vert_H,\quad n\ge 0....
This result states that every contraction on a Hilbert space has a unitary dilationUnitary dilation
In operator theory, a dilation of an operator T on a Hilbert space H is an operator on a larger Hilbert space K , whose restriction to H is T....
with the minimality property.
Application
In quantum information theory, quantum channelQuantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
s, or quantum operation
Quantum operation
In quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
s, are defined to be completely positive maps between C*-algebras. Being a classification for all such maps, Stinespring's theorem is important in that context. For example, the uniqueness part of the theorem has been used to classify certain classes of quantum channels.
For the comparison of different channels and computation of their mutual fidelities and information another representation of the channels by their "Radon-Nikodym" derivatives introduced by Belavkin is useful. In the finite dimensional case, Choi's theorem as the tracial variant of the Belavkin's Radon-Nikodym theorem for completely positive maps is also relevant. The operators
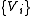from the expression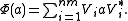are called the Kraus operators of Φ. The expression
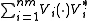
is sometimes called the operator sum representation of Φ.