Unitary dilation
Encyclopedia
In operator theory
, a dilation of an operator T on a Hilbert space
H is an operator on a larger Hilbert space K , whose restriction to H is T.
More formally, let T be a bounded operator on some Hilbert space H, and H be a subspace of a larger Hilbert space H' . A bounded operator V on H' is a dilation of T if
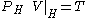
where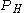
is projection on H.
V is said to be a unitary dilation (respectively, normal, isometric, etc) if V is unitary (respectively, normal, isometric, etc). T is said to be a compression of V. If an operator T has a spectral set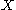
, we say that V is a normal boundary dilation or a normal 
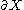dilation if V is a normal dilation of T and 
.
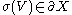Some texts impose an additional condition. Namely, that a dilation satisfy the following (calculus) property:
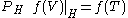
where f(T) is some specified functional calculus
(for example, the polynomial or H∞ calculus). The utility of a dilation is that it allows the "lifting" of objects associated to T to the level of V, where the lifted objects may have nicer properties. See, for example, the commutant lifting theorem
.
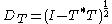
is positive, where the continuous functional calculus
is used to define the square root. The operator DT is called the defect operator of T. Let V be the operator on
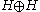
defined by the matrix
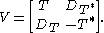
V is clearly a dilation of T. Also, T(I - T*T) = (I - TT*)T implies
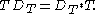
Using this one can show, by calculating directly, that V is unitary, therefore an unitary dilation of T. This operator V is sometimes called the Julia operator of T.
Notice that when T is a real scalar, say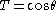
, we have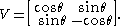
which is just the unitary matrix describing rotation by θ. For this reason, the Julia operator V(T) is sometimes called the elementary rotation of T.
We note here that in the above discussion we have not required the calculus property for a dilation. Indeed, direct calculation shows the Julia operator fails to be a "degree-2" dilation in general, i.e. it need not be true that
.
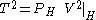However, it can also be shown that any contraction has a unitary dilation which does have the calculus property above. This is Sz.-Nagy's dilation theorem
. More generally, if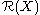
is a Dirichlet algebra
, any operator T with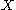
as a spectral set will have a normal 
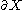dilation with this property. This generalises Sz.-Nagy's dilation theorem as all contractions have the unit disc as a spectral set.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a dilation of an operator T on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H is an operator on a larger Hilbert space K , whose restriction to H is T.
More formally, let T be a bounded operator on some Hilbert space H, and H be a subspace of a larger Hilbert space H' . A bounded operator V on H' is a dilation of T if
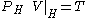
where
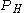is projection on H.V is said to be a unitary dilation (respectively, normal, isometric, etc) if V is unitary (respectively, normal, isometric, etc). T is said to be a compression of V. If an operator T has a spectral set
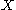, we say that V is a normal boundary dilation or a normal 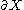dilation if V is a normal dilation of T and 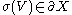.Some texts impose an additional condition. Namely, that a dilation satisfy the following (calculus) property:
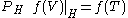
where f(T) is some specified functional calculus
Functional calculus
In mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
(for example, the polynomial or H∞ calculus). The utility of a dilation is that it allows the "lifting" of objects associated to T to the level of V, where the lifted objects may have nicer properties. See, for example, the commutant lifting theorem
Commutant lifting theorem
In operator theory, the commutant lifting theorem, due to Sz.-Nagy and Foias, states that if T is a contraction on a Hilbert space H, U is its minimal unitary dilation acting on some Hilbert space K , and R is an operator on H commuting with T, then there is an operator S on K commuting with...
.
Applications
We can show that every contraction on Hilbert spaces has a unitary dilation. A possible construction of this dilation is as follows. For a contraction T, the operator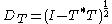is positive, where the continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
is used to define the square root. The operator DT is called the defect operator of T. Let V be the operator on
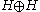
defined by the matrix
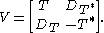
V is clearly a dilation of T. Also, T(I - T*T) = (I - TT*)T implies
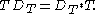
Using this one can show, by calculating directly, that V is unitary, therefore an unitary dilation of T. This operator V is sometimes called the Julia operator of T.
Notice that when T is a real scalar, say
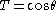, we have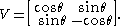which is just the unitary matrix describing rotation by θ. For this reason, the Julia operator V(T) is sometimes called the elementary rotation of T.
We note here that in the above discussion we have not required the calculus property for a dilation. Indeed, direct calculation shows the Julia operator fails to be a "degree-2" dilation in general, i.e. it need not be true that
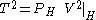.However, it can also be shown that any contraction has a unitary dilation which does have the calculus property above. This is Sz.-Nagy's dilation theorem
Sz.-Nagy's dilation theorem
The Sz.-Nagy dilation theorem states that every contraction T on a Hilbert space H has a unitary dilation U to a Hilbert space K, containing H, withT^n = P_H U^n \vert_H,\quad n\ge 0....
. More generally, if
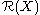is a Dirichlet algebraDirichlet algebra
In mathematics, a Dirichlet algebra is a particular type of algebra associated to a compact Hausdorff space X. It is a closed subalgebra of C, the uniform algebra of bounded continuous functions on X, whose real parts are dense in the algebra of bounded continuous real functions on X...
, any operator T with
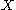as a spectral set will have a normal 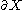dilation with this property. This generalises Sz.-Nagy's dilation theorem as all contractions have the unit disc as a spectral set.