In combinatorial

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

 mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a Steiner system (named after Jakob Steiner

Jakob Steiner

Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...

) is a type of block design. Specifically, S(l,m,n) is a -design.

A Steiner system with parameters l, m, n, written S(l,m,n), is an n-element set S together with a set of m-element subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

s of S (called blocks) with the property that each l-element subset of S is contained in exactly one block. A Steiner system with parameters l, m, n is often called simply "an S(l,m,n)".

An S(2,3,n) is called a Steiner triple system, and its blocks are called triples.
The number of triples is n(n−1)/6.
We can define a multiplication on a Steiner triple system by setting aa = a for all a in S, and ab = c if {a,b,c} is a triple. This makes S into an idempotent commutative quasigroup

Quasigroup

In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...

.

An S(3,4,n) is sometimes called a Steiner quadruple system. Systems with higher values of m are not usually called by special names.

Finite projective planes

A finite projective plane

Projective plane

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

 of order q, with the lines as blocks, is an S(2, q+1, q²+q+1), since it has q²+q+1 points, each line passes through q+1 points, and each pair of distinct points lies on exactly one line.

Properties

It is clear from the definition of S(l,m,n) that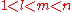 . (Equalities, while technically possible, lead to trivial systems.)

If S(l,m,n) exists, then taking all blocks containing a specific element and discarding that element gives a derived system S(l−1,m−1,n−1). Therefore the existence of S(l−1,m−1,n−1) is a necessary condition for the existence of S(l,m,n).

The number of l-element subsets in S is , while the number of l-element subsets in each block is . Since every l-element subset is contained in exactly one block, we have , or , where b is the number of blocks. Similar reasoning about l-element subsets containing a particular element gives us 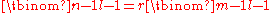, or 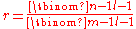, where r is the number of blocks containing any given element. From these definitions follows the equation . It is a necessary condition for the existence of S(l,m,n) that b and r are integers. As with any block design, Fisher's inequality

Fisher's inequality

In combinatorial mathematics, Fisher's inequality, named after Ronald Fisher, is a necessary condition for the existence of a balanced incomplete block design satisfying certain prescribed conditions....

  is true in Steiner systems.

It can be shown that if there is a Steiner system S(2,m,n), where m is a prime power greater than 1, then n = 1 or m (mod m(m−1)). In particular, a Steiner triple system S(2,3,n) must have n = 6k+1 or 6k+3. It is known that this is the only restriction on Steiner triple systems, that is, for each natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

 k, systems S(2,3,6k+1) and S(2,3,6k+3) exist.

History

Steiner systems were introduced in , in the form of Kirkman's schoolgirl problem

Kirkman's schoolgirl problem

Kirkman's schoolgirl problem is a problem in combinatorics proposed by Thomas Kirkman in 1850 as Query VI in The Lady's and Gentleman's Diary...

, which treats triple systems. Triple systems were introduced and further studied independently in , whence the name.

Mathieu groups

Several examples of Steiner systems are closely related to group theory

Group theory

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...

. In particular, the finite simple groups called Mathieu group

Mathieu group

In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...

s arise as automorphism groups of Steiner systems:

• The Mathieu group M₁₁ is the automorphism group of a S(4,5,11) Steiner system
• The Mathieu group M₁₂ is the automorphism group of a S(5,6,12) Steiner system
• The Mathieu group M₂₂ is the unique index 2 subgroup of the automorphism group of a S(3,6,22) Steiner system
• The Mathieu group M₂₃ is the automorphism group of a S(4,7,23) Steiner system
• The Mathieu group M₂₄ is the automorphism group of a S(5,8,24) Steiner system.

The Steiner system S(5, 6, 12)

There is a unique S(5,6,12) Steiner system; its automorphism group is the Mathieu group

Mathieu group

In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...

 M₁₂, and in that context it is denoted by W₁₂.

Constructions

To construct it, take a 12-point set and think of it as the projective line

Projective line

In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...

 over F₁₁ — in other words, the integers mod 11 together with a point called infinity. Among the integers mod 11, six are perfect squares:


Call this set a "block". From this, we may obtain other blocks by applying fractional linear transformations:


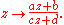
These blocks then form a (5,6,12) Steiner system.

W₁₂ can also constructed from the affine geometry

Affine geometry

In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...

 on the vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 F₃xF₃, an S(2,3,9) system.

An alternative construction of W₁₂ is the 'Kitten' of R.T. Curtis.

The Steiner system S(5, 8, 24)

Particularly remarkable is the Steiner system S(5, 8, 24), also known as the Witt design or Witt geometry. It was described in a 1931 paper by R.D. Carmichael

Robert Daniel Carmichael

Robert Daniel Carmichael was a leading American mathematician. Carmichael was born in Goodwater, Alabama. He attended Lineville College, briefly, and he earned his bachelor's degree in 1898, while he was studying towards his Ph.D. degree at Princeton University. Carmichael completed the...

 and rediscovered by Ernst Witt

Ernst Witt

Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....

, who published a paper on the subject in 1938: . This system is connected with many of the sporadic simple groups and with the exceptional

Exceptional object

Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...

 24-dimensional lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

 known as the Leech lattice

Leech lattice

In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...

.

The automorphism group of S(5, 8, 24) is the Mathieu group

Mathieu group

In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...

 M₂₄, and in that context the design is denoted W₂₄ ("W" for "Witt")

Constructions

There are many ways to construct the S(5,8,24). The method given here is perhaps the simplest to describe, and is easy to convert into a computer program. It uses sequences of 24 bits. The idea is to write these down in lexicographic order, missing out any one which differs from some earlier one in fewer than 8 positions. The result looks like this:

000000000000000000000000
000000000000000011111111
000000000000111100001111
000000000000111111110000
000000000011001100110011
000000000011001111001100
000000000011110000111100
000000000011110011000011
000000000101010101010101
000000000101010110101010
.
. (next 4083 omitted)
.
111111111111000011110000
111111111111111100000000
111111111111111111111111

The list contains 4096 items, which are each code words of the extended binary Golay code

Binary Golay code

In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....

. They form a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

under the XOR operation. One of them has zero 1-bits, 759 of them have eight 1-bits, 2576 of them have twelve 1-bits, 759 of them have sixteen 1-bits, and one has twenty-four 1-bits. The 759 8-element blocks of the S(5,8,24) (called octads) are given by the patterns of 1's in the code words with eight 1-bits.

A still more direct approach is taken by running through all 8-element subsets of a 24-element set and skipping any such subset which differs from some octad already found in fewer than four positions.

Departing from 01, 02, 03, ..., 22, 23, 24 one obtains

01 02 03 04 05 06 07 08
01 02 03 04 09 10 11 12
01 02 03 04 13 14 15 16
.
. (next 753 octads omitted)
.
13 14 15 16 17 18 19 20
13 14 15 16 21 22 23 24
17 18 19 20 21 22 23 24

Each single element occurs 253 times somewhere in some octad. Each pair occurs 77 times. Each triple occurs 21 times. Each quadruple (tetrad) occurs 5 times. Each quintuple (pentad) occurs once. Not every hexad, heptad or octad occurs.

External links

• Steiner systems by Andries E. Brouwer
• Implementation of S(5,8,24) by Dr. Alberto Delgado, Gabe Hart, and Michael Kolkebeck
• S(5, 8, 24) Software and Listing by Johan E. Mebius
• The Witt Design computed by Ashay Dharwadker