Sion's minimax theorem
Encyclopedia
In mathematics
, and in particular game theory
, Sion's minimax theorem is a generalization of John von Neumann
's minimax theorem.
It states:
Let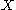
be a compact
convex
subset of a linear topological space and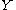
a convex subset of a linear topological space. If 
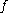is a real-valued function
on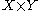
with
then,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, Sion's minimax theorem is a generalization of John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
's minimax theorem.
It states:
Let
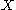be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset of a linear topological space and
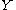a convex subset of a linear topological space. If 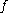is a real-valued functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on
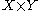with-
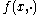upper semicontinuous and quasiconcaveQuasiconvex functionIn mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set...
on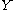
, 
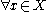, and -
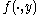is lower semicontinuous and quasi-convex on 
, 
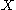then,
