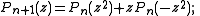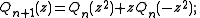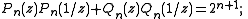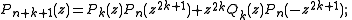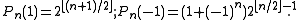Shapiro polynomials
Encyclopedia
In mathematics, the Shapiro polynomials are a sequence of polynomials
which were first studied by Harold S. Shapiro
in 1951 when considering the magnitude of specific trigonometric sums. In signal processing
, the Shapiro polynomials have good autocorrelation
properties and their values on the unit circle
are small. The first few members of the sequence are:
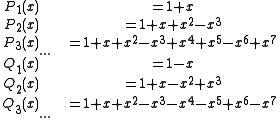
where the second sequence, indicated by Q, is said to be complementary to the first sequence, indicated by P.
The first Shapiro Pn(z) is the partial sum of order 2n − 1 (where n = 0, 1, 2, ...) of the power series
The Golay-Rudin-Shapiro sequence {an} has a fractal-like structure – for example, an = a2n – which implies that the subsequence (a0, a2, a4, ...) replicates the original sequence {an}. This in turn leads to remarkable
functional equations satisfied by f(z).
The second or complementary Shapiro polynomials Qn(z) may be defined in terms of this sequence, or by the relation Qn(z) = (1-)nz2n-1Pn(-1/z), or by the recursions
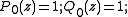
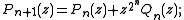
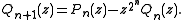
The most interesting property of the {Pn} is that the absolute value of Pn(z) is bounded on the unit circle by the square root of 2(n + 1), which is on the order
of the L2 norm of Pn. Polynomials with coefficients from the set {−1, 1} whose maximum modulus on the unit circle is close to their mean modulus are useful for various applications in communication theory (e.g., antenna design and data compression
). Property (iii) shows that (P, Q) form a Golay pair.
These polynomials have further properties: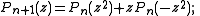
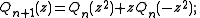
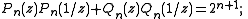
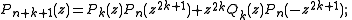
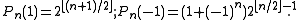
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
which were first studied by Harold S. Shapiro
Harold S. Shapiro
Harold Seymour Shapiro is a professor emeritus of mathematics at the Royal Institute of Technology in Stockholm, Sweden, best...
in 1951 when considering the magnitude of specific trigonometric sums. In signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, the Shapiro polynomials have good autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
properties and their values on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
are small. The first few members of the sequence are:
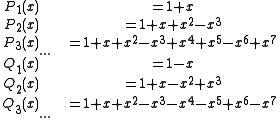
where the second sequence, indicated by Q, is said to be complementary to the first sequence, indicated by P.
Construction
The Shapiro polynomials Pn(z) may be constructed from the Golay-Rudin-Shapiro sequence an, which equals 1 if the number of pairs of consecutive ones in the binary expansion of n is even, and −1 otherwise. Thus a0 = 1, a1 = 1, a2 = 1, a3 = −1, etc.The first Shapiro Pn(z) is the partial sum of order 2n − 1 (where n = 0, 1, 2, ...) of the power series
- f(z) := a0 + a1 z + a2 z2 + ...
The Golay-Rudin-Shapiro sequence {an} has a fractal-like structure – for example, an = a2n – which implies that the subsequence (a0, a2, a4, ...) replicates the original sequence {an}. This in turn leads to remarkable
functional equations satisfied by f(z).
The second or complementary Shapiro polynomials Qn(z) may be defined in terms of this sequence, or by the relation Qn(z) = (1-)nz2n-1Pn(-1/z), or by the recursions
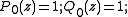
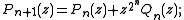
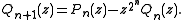
Properties
The sequence of complementary polynomials Qn corresponding to the Pn is uniquely characterized by the following properties:- (i) Qn is of degree 2n − 1;
- (ii) the coefficients of Qn are all 1 or −1 , and its constant term equals 1; and
- (iii) the identity |Pn(z)|2 + |Qn(z)|2 = 2(n + 1) holds on the unit circle, where the complex variable z has absolute value one.
The most interesting property of the {Pn} is that the absolute value of Pn(z) is bounded on the unit circle by the square root of 2(n + 1), which is on the order
of the L2 norm of Pn. Polynomials with coefficients from the set {−1, 1} whose maximum modulus on the unit circle is close to their mean modulus are useful for various applications in communication theory (e.g., antenna design and data compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
). Property (iii) shows that (P, Q) form a Golay pair.
These polynomials have further properties: