Series acceleration
Encyclopedia
In mathematics
, series acceleration is one of a collection of sequence transformations for improving the rate of convergence
of a series
. Techniques for series acceleration are often applied in numerical analysis
, where they are used to improve the speed of numerical integration
. Series acceleration techniques may also be used, for example, to obtain a variety of identities on special functions
. Thus, the Euler transform applied to the hypergeometric series
gives some of the classic, well-known hypergeometric series identities.
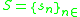
having a limit
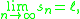
an accelerated series is a second sequence
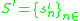
which converges faster to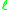
than the original sequence, in the sense that
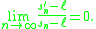
If the original sequence is divergent
, the sequence transformation acts as an extrapolation method to the antilimit
.
The mappings from the original to the transformed series may be linear (as defined in the article sequence transformations), or non-linear. In general, the non-linear sequence transformations tend to be more powerful.
, introduced by Lewis Fry Richardson
in the early 20th century but also known and used by Katahiro Takebe
in 1722, the Aitken delta-squared process, introduced by Alexander Aitken
in 1926 but also known and used by Takakazu Seki in the 18th century, the epsilon algorithm given by Peter Wynn
in 1956, the Levin u-transform, and the Wilf-Zeilberger-Ekhad method or WZ method.
For alternating series, several powerful techniques, offering convergence rates from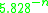
all the way to 
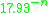for a summation of 
terms, are described by Cohen et al.. .
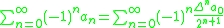
where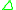
is the forward difference operator:
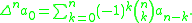
If the original series, on the left hand side, is only slowly converging, the forward differences will tend to become small quite rapidly; the additional power of two further improves the rate at which the right hand side converges.
A particularly efficient numerical implementation of the Euler transform is the van Wijngaarden transformation.
can be written as f(1), where the function f(z) is defined as
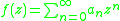
The function f(z) can have singularities in the complex plane (branch point singularities, poles or essential singularities), which limit the radius of convergence of the series. If the point z = 1 is close to or on the boundary of the disk of convergence, the series for S will converge very slowly. One can then improve the convergence of the series by means of a conformal mapping that moves the singularities such that the point that is mapped to z = 1, ends up deeper in the new disk of convergence.
The conformal transform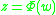
needs to be chosen such that 
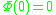, and one usually chooses a function that has a finite derivative at w = 0. One can assume that 
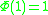without loss of generality, as one can always rescale w to redefine 
. We then consider the function
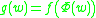
Since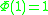
, we have f(1) = g(1). We can obtain the series expansion of g(w) by putting 
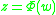in the series expansion of f(z) because 
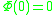; the first n terms of the series expansion for f(z) will yield the first n terms of the series expansion for g(w) if 
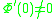. Putting w = 1 in that series expansion will thus yield a series such that if it converges, it will converge to the same value as the original series.
s and Levin-type sequence transformations.
Especially nonlinear sequence transformations often provide powerful numerical methods for the summation
of divergent series
or asymptotic series that arise for instance in perturbation theory
, and may be used as highly effective extrapolation methods.
A simple nonlinear sequence transformation is the Aitken extrapolation or delta-squared method,
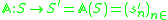
defined by
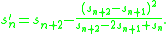
This transformation is commonly used to improve the rate of convergence
of a slowly converging sequence; heuristically, it eliminates the largest part of the absolute error.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, series acceleration is one of a collection of sequence transformations for improving the rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. Techniques for series acceleration are often applied in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, where they are used to improve the speed of numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
. Series acceleration techniques may also be used, for example, to obtain a variety of identities on special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
. Thus, the Euler transform applied to the hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
gives some of the classic, well-known hypergeometric series identities.
Definition
Given a sequence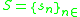having a limit
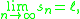
an accelerated series is a second sequence
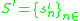
which converges faster to
than the original sequence, in the sense that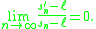If the original sequence is divergent
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, the sequence transformation acts as an extrapolation method to the antilimit
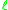.The mappings from the original to the transformed series may be linear (as defined in the article sequence transformations), or non-linear. In general, the non-linear sequence transformations tend to be more powerful.
Overview
Two classical techniques for series acceleration are Euler's transformation of series and Kummer's transformation of series. A variety of much more rapidly convergent and special-case tools have been developed in the 20th century, including Richardson extrapolationRichardson extrapolation
In numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....
, introduced by Lewis Fry Richardson
Lewis Fry Richardson
Lewis Fry Richardson, FRS was an English mathematician, physicist, meteorologist, psychologist and pacifist who pioneered modern mathematical techniques of weather forecasting, and the application of similar techniques to studying the causes of wars and how to prevent them...
in the early 20th century but also known and used by Katahiro Takebe
Takebe Kenko
, also known as Takebe Kenkō, was a Japanese mathematician in the Edo period.-Biography:Takebe was the favorite student of Seki Takakazu Takebe is considered to have extended and disseminated Seki's work....
in 1722, the Aitken delta-squared process, introduced by Alexander Aitken
Alexander Aitken
Alexander Craig Aitken was one of New Zealand's greatest mathematicians. He studied for a PhD at the University of Edinburgh, where his dissertation, "Smoothing of Data", was considered so impressive that he was awarded a DSc in 1926, and was elected a fellow of the Royal Society of Edinburgh...
in 1926 but also known and used by Takakazu Seki in the 18th century, the epsilon algorithm given by Peter Wynn
Peter Wynn (mathematician)
Peter Wynn is a mathematician. His main achievements concern approximation theory – in particular the theory of Padé approximants – and its application in numerical methods for improving the rate of convergence of sequences of real numbers....
in 1956, the Levin u-transform, and the Wilf-Zeilberger-Ekhad method or WZ method.
For alternating series, several powerful techniques, offering convergence rates from
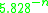all the way to 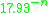for a summation of terms, are described by Cohen et al.. .Euler's transform
A basic example of a linear sequence transformation, offering improved convergence, is Euler's transform. It is intended to be applied to an alternating series; it is given by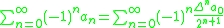where
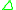is the forward difference operator: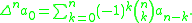If the original series, on the left hand side, is only slowly converging, the forward differences will tend to become small quite rapidly; the additional power of two further improves the rate at which the right hand side converges.
A particularly efficient numerical implementation of the Euler transform is the van Wijngaarden transformation.
Conformal mappings
A series- S =
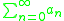
can be written as f(1), where the function f(z) is defined as
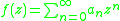
The function f(z) can have singularities in the complex plane (branch point singularities, poles or essential singularities), which limit the radius of convergence of the series. If the point z = 1 is close to or on the boundary of the disk of convergence, the series for S will converge very slowly. One can then improve the convergence of the series by means of a conformal mapping that moves the singularities such that the point that is mapped to z = 1, ends up deeper in the new disk of convergence.
The conformal transform
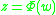needs to be chosen such that 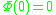, and one usually chooses a function that has a finite derivative at w = 0. One can assume that 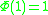without loss of generality, as one can always rescale w to redefine . We then consider the function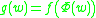Since
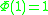, we have f(1) = g(1). We can obtain the series expansion of g(w) by putting 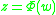in the series expansion of f(z) because 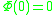; the first n terms of the series expansion for f(z) will yield the first n terms of the series expansion for g(w) if 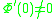. Putting w = 1 in that series expansion will thus yield a series such that if it converges, it will converge to the same value as the original series.Non-linear sequence transformations
Examples of such nonlinear sequence transformations are Padé approximantPadé approximant
Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....
s and Levin-type sequence transformations.
Especially nonlinear sequence transformations often provide powerful numerical methods for the summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
of divergent series
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
or asymptotic series that arise for instance in perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, and may be used as highly effective extrapolation methods.
Aitken method
-
- Main article: Aitken's delta-squared processAitken's delta-squared processIn numerical analysis, Aitken's delta-squared process is a series acceleration method, used for accelerating the rate of convergence of a sequence. It is named after Alexander Aitken, who introduced this method in 1926. Its early form was known to Seki Kōwa and was found for rectification of the...
- Main article: Aitken's delta-squared process
A simple nonlinear sequence transformation is the Aitken extrapolation or delta-squared method,
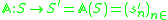
defined by
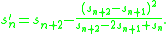
This transformation is commonly used to improve the rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
of a slowly converging sequence; heuristically, it eliminates the largest part of the absolute error.