
Semi-elliptic operator
Encyclopedia
In mathematics
— specifically, in the theory of partial differential equation
s — a semi-elliptic operator is a partial differential operator satisfying a positivity condition slightly weaker than that of being an elliptic operator
. Every elliptic operator is also semi-elliptic, and semi-elliptic operators share many of the nice properties of elliptic operators: for example, much of the same existence and uniqueness theory is applicable, and semi-elliptic Dirichlet problem
s can be solved using the methods of stochastic analysis
.
al Euclidean space
Rn, acting on suitable functions f by
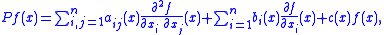
is said to be semi-elliptic if all the eigenvalues λi(x), 1 ≤ i ≤ n, of the matrix
a(x) = (aij(x)) are non-negative. (By way of contrast, P is said to be elliptic if λi(x) > 0 for all x ∈ Ω and 1 ≤ i ≤ n, and uniformly elliptic if the eigenvalues are uniformly bounded away from zero, uniformly in i and x.) Equivalently, P is semi-elliptic if the matrix a(x) is positive semi-definite
for each x ∈ Ω.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in the theory of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s — a semi-elliptic operator is a partial differential operator satisfying a positivity condition slightly weaker than that of being an elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
. Every elliptic operator is also semi-elliptic, and semi-elliptic operators share many of the nice properties of elliptic operators: for example, much of the same existence and uniqueness theory is applicable, and semi-elliptic Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
s can be solved using the methods of stochastic analysis
Stochastic processes and boundary value problems
In mathematics, some boundary value problems can be solved using the methods of stochastic analysis. Perhaps the most celebrated example is Shizuo Kakutani's 1944 solution of the Dirichlet problem for the Laplace operator using Brownian motion...
.
Definition
A second-order partial differential operator P defined on an open subset Ω of n-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, acting on suitable functions f by
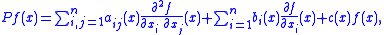
is said to be semi-elliptic if all the eigenvalues λi(x), 1 ≤ i ≤ n, of the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
a(x) = (aij(x)) are non-negative. (By way of contrast, P is said to be elliptic if λi(x) > 0 for all x ∈ Ω and 1 ≤ i ≤ n, and uniformly elliptic if the eigenvalues are uniformly bounded away from zero, uniformly in i and x.) Equivalently, P is semi-elliptic if the matrix a(x) is positive semi-definite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
for each x ∈ Ω.

