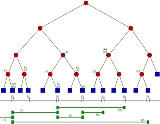
Segment tree
Encyclopedia
In computer science
, a segment tree is a tree
data structure
for storing intervals
, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, its content cannot be modified once the structure is built. A similar data structure is the interval tree
.
A segment tree for a set I of n intervals uses O
(n log n) storage and can be built in O(n log n) time. Segment trees support searching for all the intervals that contain a query point in O(log n + k), k being the number of retrieved intervals or segments.
Applications of the segment tree are in the areas of computational geometry
, and geographic information systems.
The segment tree can be generalized to higher dimension
spaces as well.
Let S be a set of intervals, or segments. Let p1, p2, ..., pm be the list of distinct interval endpoints, sorted from left to right. Consider the partitioning of the real line induced by those points. The regions of this partitioning are called elementary intervals. Thus, the elementary intervals are, from left to right:
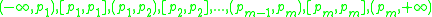
That is, the list of elementary intervals consists of open intervals between two consecutive endpoints pi and pi+1, alternated with closed intervals consisting of a single endpoint. Single points are treated themselves as intervals because the answer to a query is not necessarily the same at the interior of an elementary interval and its endpoints.
 Given a set I of intervals, or segments, a segment tree T for I is structured as follows:
Given a set I of intervals, or segments, a segment tree T for I is structured as follows:
A segment tree T on a set I of n intervals uses O(nlogn) storage.
A segment tree from the set of segments I, can be built as follows. First, the endpoints of the intervals in I are sorted. The elementary intervals are obtained from that. Then, a balanced binary tree is built on the elementary intervals, and for each node v it is determined the interval Int(v) it represents. It remains to compute the canonical subsets for the nodes. To achieve this, the intervals in I are inserted one by one into the segment tree. An interval X = [x, x′] can be inserted in a subtree rooted at T, using the following procedure :
The complete construction operation takes O(nlogn) time, being n the amount of segments in I.
A query for a segment tree, receives a point qx, and retrieves a list of all the segments stored which contain the point qx.
Formally stated; given a node (subtree) v and a query point qx, the query can be done using the following algorithm:
In a segment tree that contains n intervals, those containing a given query point can be reported in O(logn + k) time, where k is the number of reported intervals.
The use of fractional cascading
lowers the query time bound by a logarithmic factor. The use of the interval tree
on the deepest level of associated structures lowers the storage bound with a logarithmic factor.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a segment tree is a tree
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
for storing intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, its content cannot be modified once the structure is built. A similar data structure is the interval tree
Interval tree
In computer science, an interval tree is an ordered tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for example, to find all roads on a computerized map inside...
.
A segment tree for a set I of n intervals uses O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n log n) storage and can be built in O(n log n) time. Segment trees support searching for all the intervals that contain a query point in O(log n + k), k being the number of retrieved intervals or segments.
Applications of the segment tree are in the areas of computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, and geographic information systems.
The segment tree can be generalized to higher dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
spaces as well.
Structure description
This section describes the structure of a segment tree in a one-dimensional space.Let S be a set of intervals, or segments. Let p1, p2, ..., pm be the list of distinct interval endpoints, sorted from left to right. Consider the partitioning of the real line induced by those points. The regions of this partitioning are called elementary intervals. Thus, the elementary intervals are, from left to right:
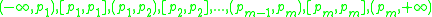
That is, the list of elementary intervals consists of open intervals between two consecutive endpoints pi and pi+1, alternated with closed intervals consisting of a single endpoint. Single points are treated themselves as intervals because the answer to a query is not necessarily the same at the interior of an elementary interval and its endpoints.

- T is a binary treeBinary treeIn computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
. - Its leafs correspond to the elementary intervals induced by the endpoints in I, in an ordered way: the leftmost leaf corresponds to the leftmost interval, and so on. The elementary interval corresponding to a leaf v is denoted Int(v).
- The internal nodes of T corresponds to intervals that are the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of elementary intervals: the interval Int(N) corresponding to node N is the union of the intervals corresponding to the leafs of the tree rooted at N. That implies that Int(N) is the union of the intervals of its two children. - Each node or leaf v in T stores the interval Int(v) and a set of intervals, in some data structure. This canonical subset of node v contains the intervals [x, x′] from I such that [x, x′] contains Int(v) and does not contain Int(parent(v)). That is, each segment in I stores the segments that span through its interval, but do not span through the interval of its parent.
Storage requirements
This section analyzes the storage cost of a segment tree in a one-dimensional space.A segment tree T on a set I of n intervals uses O(nlogn) storage.
- Proof:
- Lemma: Any interval [x, x′] of I is stored in the canonical set for at most two nodes at the same depth.
-
- Proof: Let v1, v2, v3 be the three nodes at the same depth, numbered from left to right; and let w be the parent node of v2. Suppose [x, x′] is stored at v1 and v3. This means that [x, x′] spans the whole interval from the left endpoint of Int(v1) to the right endpoint of Int(v3). Because v2 lies between v1 and v3, Int(w) must be contained in [x, x′]. Hence, [x, x′] will not be stored at v2.
- The set I has at most 4n + 1 elementary intervals. Because T is a binary balanced tree with at most 4n + 1 leaves, its height is O(logn). Since any interval is stored at most twice at a given depth of the tree, that the total amount of storage is O(nlogn).
Construction
This section describes the construction of a segment tree in a one-dimensional space.A segment tree from the set of segments I, can be built as follows. First, the endpoints of the intervals in I are sorted. The elementary intervals are obtained from that. Then, a balanced binary tree is built on the elementary intervals, and for each node v it is determined the interval Int(v) it represents. It remains to compute the canonical subsets for the nodes. To achieve this, the intervals in I are inserted one by one into the segment tree. An interval X = [x, x′] can be inserted in a subtree rooted at T, using the following procedure :
- If Int(T) is contained in X then store X at T, and finish.
- Else:
- If X intersects the canonical subset of the left child of T, then insert X in that child, recursively.
- If X intersects the canonical subset of the right child of T, then insert X in that child, recursively.
The complete construction operation takes O(nlogn) time, being n the amount of segments in I.
- Proof
- Sorting the endpoints takes O(nlogn). Building a balanced binary tree from the sorted endpoints, takes linear time on n.
- The insertion of an interval X = [x, x′] into the tree, costs O(logn).
- Proof: Visiting every node takes constant time (assuming that canonical subsets are stored in a simple data structure like a linked listLinked listIn computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...
). When we visit node v, we either store X at v, or Int(v) contains an endpoint of X. As proved above, an interval is stored at most twice at each level of the tree. There is also at most one node at every level whose corresponding interval contains x, and one node whose interval contains x′. So, at most four nodes per level are visited. Since there are O(logn) levels, the total cost of the insertion is O(logn).
- Proof: Visiting every node takes constant time (assuming that canonical subsets are stored in a simple data structure like a linked list
Query
This section describes the query operation of a segment tree in a one-dimensional space.A query for a segment tree, receives a point qx, and retrieves a list of all the segments stored which contain the point qx.
Formally stated; given a node (subtree) v and a query point qx, the query can be done using the following algorithm:
- Report all the intervals in I(v).
- If v is not a leaf:
- If qx is in Int(left child of v) then
- Perform a query in the left child of v.
- Else
- Perform a query in the right child of v.
- If qx is in Int(left child of v) then
In a segment tree that contains n intervals, those containing a given query point can be reported in O(logn + k) time, where k is the number of reported intervals.
- Proof: The query algorithm visits one node per level of the tree, so O(logn) nodes in total. In the other hand, at a node v, the segments in I are reported in O(1 + kv) time, where kv is the number of intervals at node v, reported. The sum of all the kv for all nodes v visited, is k, the number of reported segments.
Generalization for higher dimensions
The segment tree can be generalized to higher dimension spaces, in the form of multi-level segment trees. In higher dimension versions, the segment tree stores a collection of axis-parallel (hyper-)rectangles, and can retrieve the rectangles that contain a given query point. The structure uses O(nlogd-1n) storage, and answers queries in O(logdn).The use of fractional cascading
Fractional cascading
In computer science, fractional cascading is a technique to speed up a sequence of binary searches for the same value in a sequence of related data structures. The first binary search in the sequence takes a logarithmic amount of time, as is standard for binary searches, but successive searches in...
lowers the query time bound by a logarithmic factor. The use of the interval tree
Interval tree
In computer science, an interval tree is an ordered tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for example, to find all roads on a computerized map inside...
on the deepest level of associated structures lowers the storage bound with a logarithmic factor.

