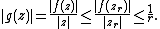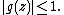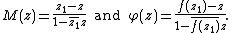Schwarz lemma
Encyclopedia
In mathematics
, the Schwarz lemma, named after Hermann Amandus Schwarz, is a result in complex analysis
about holomorphic functions from the open
unit disk to itself. The lemma is less celebrated than stronger theorems, such as the Riemann mapping theorem, which it helps to prove. It is however one of the simplest results capturing the rigidity of holomorphic functions.
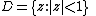be the open unit disk in the complex plane
C centered at the origin
and let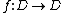
be a holomorphic map such that 
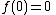and 
for all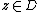 
.
Then,
for all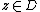 
and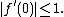 
Moreover, if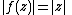
for some 
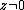or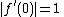 
then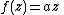
for some 
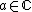with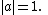 
on the function
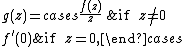
which is holomorphic on the whole of D, including at the origin (because f is differentiable at the origin and fixes zero). Now if
denotes the closed disk of radius r centered at the origin, then the maximum modulus principle implies that, for r < 1, given any z in Dr, there exists zr on the boundary of Dr such that
As r approaches 1 we get
Moreover, suppose that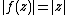
for some nonzero 
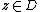, or 
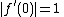. Then, 
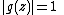at some point of 
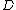. So by the maximum modulus principle, 
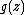is equal to a constant 
such that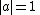 
. Therefore, 
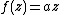, as desired.
Let ƒ : D → D be holomorphic. Then, for all z1, z2 ∈ D,
and, for all z ∈ D,
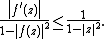
The expression
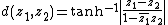
is the distance of the points z1, z2 in the Poincaré metric
, i.e. the metric in the Poincaré disc model for hyperbolic geometry
in dimension two. The Schwarz–Pick theorem then essentially states that a holomorphic map of the unit disk into itself decreases the distance of points in the Poincaré metric. If equality holds throughout in one of the two inequalities above (which is equivalent to saying that the holomorphic map preserves the distance in the Poincaré metric) , then ƒ must be an analytic automorphism of the unit disc, given by a Möbius transformation mapping the unit disc to itself.
An analogous statement on the upper half-plane H can be made as follows:
Let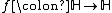
be holomorphic. Then, for all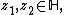 
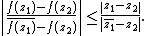
This is an easy consequence of the Schwarz–Pick theorem mentioned above: One just needs to remember that the Cayley transform
W(z) = (z − i)/(z + i) maps the upper half-plane H conformally onto the unit disc D. Then, the map W o ƒ o W−1 is a holomorphic map from D onto D. Using the Schwarz–Pick theorem on this map, and finally simplifying the results by using the formula for W, we get the desired result. Also, for all z ∈ H,
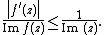
If equality holds for either the one or the other expressions, then ƒ must be a Möbius transformation with real coefficients. That is, if equality holds, then
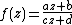
with a, b, c, d being real numbers, and ad − bc > 0.
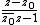where |z0| < 1 maps the unit circle to itself. Fix z1 and define the Möbius transformations
Since M(z1) = 0 and the Möbius transformation is invertible, the composition φ(ƒ(M −1(z))) maps 0 to 0 and the unit disk is mapped into itself. Thus we can apply Schwarz's lemma, which is to say
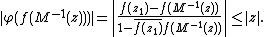
Now calling z2 = M −1(z) (which will still be in the unit disk) yields the desired conclusion
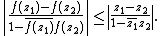
To prove the second part of the theorem, we just let z2 tend to z1.
provides an analogous theorem for hyperbolic manifolds.
De Branges' theorem
, formerly known as the Bieberbach Conjecture, is an important extension of the lemma, giving restrictions on the higher derivatives of ƒ at 0 in case ƒ is injective; that is, univalent.
The Koebe 1/4 theorem
provides a related estimate in the case that ƒ is univalent.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Schwarz lemma, named after Hermann Amandus Schwarz, is a result in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
about holomorphic functions from the open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
unit disk to itself. The lemma is less celebrated than stronger theorems, such as the Riemann mapping theorem, which it helps to prove. It is however one of the simplest results capturing the rigidity of holomorphic functions.
Statement
Let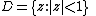 be the open unit disk in the complex planeComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
C centered at the origin
Origin
Origin, origins, or original may refer to:- Beginning of the universe and life :* Abiogenesis, the study of how life on Earth arose from inanimate matter* Cosmogony, any theory concerning the origin of the universe...
and let
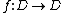be a holomorphic map such that 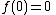and for all 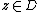.Then,
for all 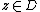and 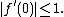Moreover, if
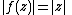for some 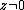or 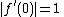then
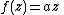for some 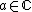with 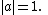Proof
The proof is a straightforward application of the maximum modulus principleMaximum modulus principle
In mathematics, the maximum modulus principle in complex analysis states that if f is a holomorphic function, then the modulus |f| cannot exhibit a true local maximum that is properly within the domain of f....
on the function
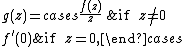
which is holomorphic on the whole of D, including at the origin (because f is differentiable at the origin and fixes zero). Now if
denotes the closed disk of radius r centered at the origin, then the maximum modulus principle implies that, for r < 1, given any z in Dr, there exists zr on the boundary of Dr such that
As r approaches 1 we get
Moreover, suppose that
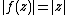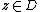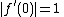for some nonzero , or . Then, 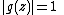at some point of 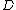. So by the maximum modulus principle, 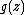is equal to a constant such that 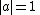. Therefore, 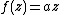, as desired.Schwarz–Pick theorem
A variant of the Schwarz lemma can be stated that is invariant under analytic automorphisms on the unit disk, i.e. bijective holomorphic mappings of the unit disc to itself. This variant is known as the Schwarz–Pick theorem (after Georg Pick):Let ƒ : D → D be holomorphic. Then, for all z1, z2 ∈ D,
and, for all z ∈ D,
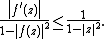
The expression
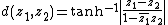
is the distance of the points z1, z2 in the Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
, i.e. the metric in the Poincaré disc model for hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
in dimension two. The Schwarz–Pick theorem then essentially states that a holomorphic map of the unit disk into itself decreases the distance of points in the Poincaré metric. If equality holds throughout in one of the two inequalities above (which is equivalent to saying that the holomorphic map preserves the distance in the Poincaré metric) , then ƒ must be an analytic automorphism of the unit disc, given by a Möbius transformation mapping the unit disc to itself.
An analogous statement on the upper half-plane H can be made as follows:
Let
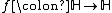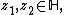
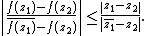
be holomorphic. Then, for all This is an easy consequence of the Schwarz–Pick theorem mentioned above: One just needs to remember that the Cayley transform
Cayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
W(z) = (z − i)/(z + i) maps the upper half-plane H conformally onto the unit disc D. Then, the map W o ƒ o W−1 is a holomorphic map from D onto D. Using the Schwarz–Pick theorem on this map, and finally simplifying the results by using the formula for W, we get the desired result. Also, for all z ∈ H,
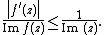
If equality holds for either the one or the other expressions, then ƒ must be a Möbius transformation with real coefficients. That is, if equality holds, then
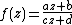
with a, b, c, d being real numbers, and ad − bc > 0.
Proof of Schwarz–Pick theorem
The proof of the Schwarz–Pick theorem follows from Schwarz's lemma and the fact that a Möbius transformation of the form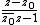 where |z0| < 1 maps the unit circle to itself. Fix z1 and define the Möbius transformations
Since M(z1) = 0 and the Möbius transformation is invertible, the composition φ(ƒ(M −1(z))) maps 0 to 0 and the unit disk is mapped into itself. Thus we can apply Schwarz's lemma, which is to say
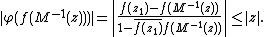
Now calling z2 = M −1(z) (which will still be in the unit disk) yields the desired conclusion
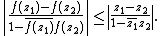
To prove the second part of the theorem, we just let z2 tend to z1.
Further generalizations and related results
The Schwarz–Ahlfors–Pick theoremSchwarz–Ahlfors–Pick theorem
In mathematics, the Schwarz–Ahlfors–Pick theorem is an extension of the Schwarz lemma for hyperbolic geometry, such as the Poincaré half-plane model...
provides an analogous theorem for hyperbolic manifolds.
De Branges' theorem
De Branges' theorem
In complex analysis, the Bieberbach conjecture or de Branges's theorem, posed by and proven by , states a necessary condition on a holomorphic function to map the open unit disk of the complex plane injectively to the complex plane....
, formerly known as the Bieberbach Conjecture, is an important extension of the lemma, giving restrictions on the higher derivatives of ƒ at 0 in case ƒ is injective; that is, univalent.
The Koebe 1/4 theorem
Koebe 1/4 theorem
In complex analysis, a branch of mathematics, the Koebe 1/4 theorem states that the image of an injective analytic function f:\mathbb D\to\mathbb C from the unit disk \mathbb D onto a subset of the complex plane contains the disk whose center is f\, and whose radius is |f\,'|/4. The theorem is...
provides a related estimate in the case that ƒ is univalent.