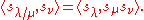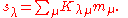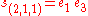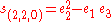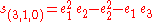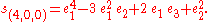Schur polynomial
Encyclopedia
In mathematics
, Schur polynomials, named after Issai Schur
, are certain symmetric polynomial
s in n variables, indexed by partitions, that generalize the elementary symmetric polynomial
s and the complete homogeneous symmetric polynomial
s. In representation theory
they are the characters of irreducible representations of the general linear group
s. The Schur polynomials form a linear basis
for the space of all symmetric polynomials. Any product of Schur functions can be written as a linear combination of Schur polynomials with non-negative integral coefficients; the values of these coefficients is given combinatorially by the Littlewood-Richardson rule. More generally, skew Schur polynomials are associated with pairs of partitions and have similar properties to Schur polynomials.

(where each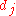 is a non-negative integer), the following functions are alternating polynomials (in other words they change sign under any transposition of the variables):
is a non-negative integer), the following functions are alternating polynomials (in other words they change sign under any transposition of the variables):
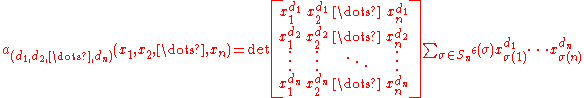
Since they are alternating, they are all divisible by the Vandermonde determinant:

The Schur polynomials are defined as the ratio: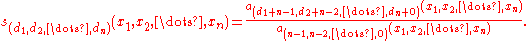
This is a symmetric function because the numerator and denominator are both alternating, and a polynomial since all alternating polynomials are divisible by the Vandermonde determinant.
The first Giambelli formula gives explicit expression of Schur polynomials as a polynomial
in the complete homogeneous symmetric polynomial
s:

The second Giambelli formula gives explicit expression of Schur polynomials as polynomials in the elementary symmetric polynomial
s:

where is a dual partition to
is a dual partition to 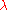
These two formulas are also known as "determinantal formulas" and the first one is known as the Jacobi-Trudy identity.
For a partition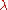 , the Schur function is a sum of monomials:
, the Schur function is a sum of monomials:
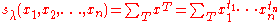
where the summation is over all semistandard Young tableau
x of shape
of shape 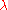 ; the exponents
; the exponents  give the weight of
give the weight of  , in other words each
, in other words each 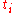 counts the occurrences of the number
counts the occurrences of the number 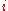 in
in  . This can be shown to be equivalent to the definition from the first Giambelli formula using the Lindström–Gessel–Viennot lemma
. This can be shown to be equivalent to the definition from the first Giambelli formula using the Lindström–Gessel–Viennot lemma
(as outlined on that page).
Schur polynomials sλ can be expressed as linear combinations of monomial
symmetric function
s mμ with non-negative integer coefficients Kλμ called Kostka number
s:
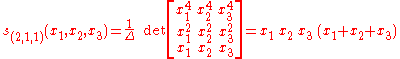
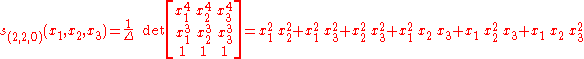
and so forth. Summarizing:
Every homogeneous degree-four symmetric polynomial in three variables can be expressed as a unique linear combination of these four Schur polynomials, and this combination can again be found using a Gröbner basis for an appropriate elimination order. For example,

is obviously a symmetric polynomial which is homogeneous of degree four, and we have
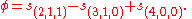
s, general linear group
s, and unitary group
s, and in fact this is how they arose. The Weyl character formula
implies that the Schur polynomials are the characters of finite dimensional irreducible representations of the general linear groups, and helps to generalize Schur's work to other compact and semisimple Lie group
s.
Several expressions arise for this relation, one of the most important being the expansion of the Schur functions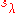 in terms of the symmetric power functions
in terms of the symmetric power functions 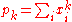 . If we write
. If we write 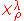 for the character of the representation of the symmetric group indexed by the partition
for the character of the representation of the symmetric group indexed by the partition 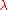 evaluated at elements of cycle type indexed by the partition
evaluated at elements of cycle type indexed by the partition 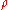 , then
, then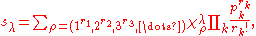
where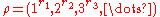 means that the partition
means that the partition 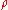 has
has 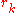 parts of length
parts of length 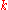 .
.
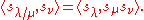
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Schur polynomials, named after Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
, are certain symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s in n variables, indexed by partitions, that generalize the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s and the complete homogeneous symmetric polynomial
Complete homogeneous symmetric polynomial
In mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials...
s. In representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
they are the characters of irreducible representations of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
s. The Schur polynomials form a linear basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the space of all symmetric polynomials. Any product of Schur functions can be written as a linear combination of Schur polynomials with non-negative integral coefficients; the values of these coefficients is given combinatorially by the Littlewood-Richardson rule. More generally, skew Schur polynomials are associated with pairs of partitions and have similar properties to Schur polynomials.
Definition
Schur polynomials correspond to integer partitions. Given a partition
(where each
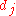 is a non-negative integer), the following functions are alternating polynomials (in other words they change sign under any transposition of the variables):
is a non-negative integer), the following functions are alternating polynomials (in other words they change sign under any transposition of the variables):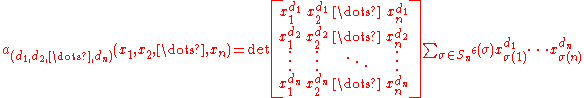
Since they are alternating, they are all divisible by the Vandermonde determinant:

The Schur polynomials are defined as the ratio:
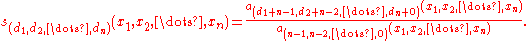
This is a symmetric function because the numerator and denominator are both alternating, and a polynomial since all alternating polynomials are divisible by the Vandermonde determinant.
Properties
The degree d Schur polynomials in n variables are a linear basis for the space of homogeneous degree d symmetric polynomials in n variables.The first Giambelli formula gives explicit expression of Schur polynomials as a polynomial
in the complete homogeneous symmetric polynomial
Complete homogeneous symmetric polynomial
In mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials...
s:

The second Giambelli formula gives explicit expression of Schur polynomials as polynomials in the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s:

where
 is a dual partition to
is a dual partition to 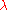
These two formulas are also known as "determinantal formulas" and the first one is known as the Jacobi-Trudy identity.
For a partition
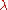 , the Schur function is a sum of monomials:
, the Schur function is a sum of monomials: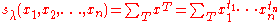
where the summation is over all semistandard Young tableau
Young tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x
 of shape
of shape 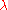 ; the exponents
; the exponents  give the weight of
give the weight of  , in other words each
, in other words each 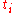 counts the occurrences of the number
counts the occurrences of the number 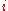 in
in  . This can be shown to be equivalent to the definition from the first Giambelli formula using the Lindström–Gessel–Viennot lemma
. This can be shown to be equivalent to the definition from the first Giambelli formula using the Lindström–Gessel–Viennot lemmaLindström–Gessel–Viennot lemma
In mathematics, the Lindström–Gessel–Viennot lemma provides a way to count the number of tuples of non-intersecting lattice paths.- Statement :...
(as outlined on that page).
Schur polynomials sλ can be expressed as linear combinations of monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s mμ with non-negative integer coefficients Kλμ called Kostka number
Kostka number
In mathematics, a Kostka number Kλμ, introduced by , is a non-negative integer depending on two partitions λ and μ, that is equal to the number of semistandard Young tableaux of shape λ and weight μ....
s:
Example
The following extended example should help clarify these ideas. Consider the case n = 3, d = 4. Using Ferrers diagrams or some other method, we find that there are just four partitions of 4 into at most three parts. We have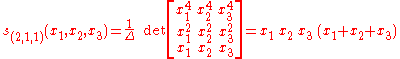
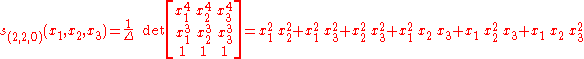
and so forth. Summarizing:
Every homogeneous degree-four symmetric polynomial in three variables can be expressed as a unique linear combination of these four Schur polynomials, and this combination can again be found using a Gröbner basis for an appropriate elimination order. For example,

is obviously a symmetric polynomial which is homogeneous of degree four, and we have
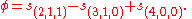
Relation to representation theory
The Schur polynomials occur in the representation theory of the symmetric groupRepresentation theory of the symmetric group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to problems of quantum...
s, general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
s, and unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
s, and in fact this is how they arose. The Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
implies that the Schur polynomials are the characters of finite dimensional irreducible representations of the general linear groups, and helps to generalize Schur's work to other compact and semisimple Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s.
Several expressions arise for this relation, one of the most important being the expansion of the Schur functions
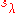 in terms of the symmetric power functions
in terms of the symmetric power functions 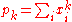 . If we write
. If we write 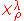 for the character of the representation of the symmetric group indexed by the partition
for the character of the representation of the symmetric group indexed by the partition 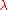 evaluated at elements of cycle type indexed by the partition
evaluated at elements of cycle type indexed by the partition 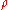 , then
, then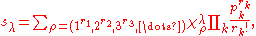
where
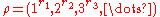 means that the partition
means that the partition 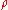 has
has 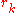 parts of length
parts of length 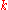 .
.Skew Schur functions
Skew Schur functions sλ/μ depend on two partitions λ and μ, and can be defined by the property