
Complete homogeneous symmetric polynomial
Encyclopedia
In mathematics
, specifically in algebraic combinatorics
and commutative algebra
, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomial
s. Every symmetric polynomial can be expressed as a polynomial expression in complete homogeneous symmetric polynomials.
 variables X1, ..., Xn, written hk for k = 0, 1, 2, ..., is the sum of all monomial
variables X1, ..., Xn, written hk for k = 0, 1, 2, ..., is the sum of all monomial
s of total degree k in the variables. Formally,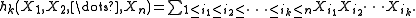
The first few of these polynomials are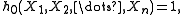
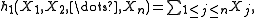
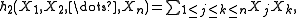

Thus, for each nonnegative integer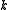 , there exists exactly one complete homogeneous symmetric polynomial of degree
, there exists exactly one complete homogeneous symmetric polynomial of degree 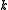 in
in  variables.
variables.
The polynomial ring
formed by taking all integral linear combinations of products of the complete homogeneous symmetric polynomials is a commutative ring.
 basic (as explained below) complete homogeneous symmetric polynomials for the first three positive values of n.
basic (as explained below) complete homogeneous symmetric polynomials for the first three positive values of n.
For n = 1:
For n = 2: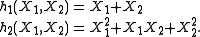
For n = 3: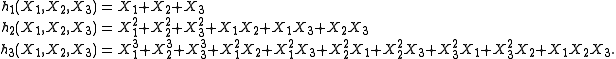
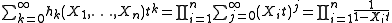
(this is called the generating function
, or generating series, for the complete homogeneous symmetric polynomials).
Here each fraction in the final expression is the usual way to represent the formal geometric series that is a factor in the middle expression. The identity can be justified by considering how the product of those geometric series is formed: each term of the product is obtained by multiplying one term chosen from each geometric series, and every monomial in the variables Xi is obtained for exactly one such choice of terms, and comes multiplied by a power of t equal to the degree of the monomial.
There is a fundamental relation between the elementary symmetric polynomials and the complete homogeneous ones:
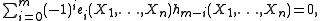
which is valid for all m > 0, and any number of variables n. The easiest way to see that it holds is from an identity of formal power series in t for the elementary symmetric polynomials, analogous to the one given above for the complete homogeneous ones:
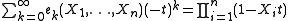
(this is actually an identity of polynomials in t, because after en(X1,…Xn) the elementary symmetric polynomials become zero). Multiplying this by the generating function for the complete homogeneous symmetric polynomials, one obtains the constant series 1, and the relation between the elementary and complete homogeneous polynomials follows from comparing coefficients of tm. A somewhat more direct way to understand that relation, is to consider the contributions in the summation involving a fixed monomial Xα of degree m. For any subset S of the variables appearing with nonzero exponent in the monomial, there is a contribution involving the product XS of those variables as term from es(X1,…,Xn), where s = #S, and the monomial Xα / XS from hm−s(X1,…,Xn); this contribution has coefficient (−1)s. The relation then follows from the fact that
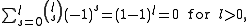
by the binomial formula, where l ≤ m denotes the number of distinct variables occurring (with nonzero exponent) in Xα.
Since e0(X1, …, Xn) and h0(X1, …, Xn) are both equal to 1, one can isolate from the relation either the first or the last terms of the summation. The former gives a sequence of equations
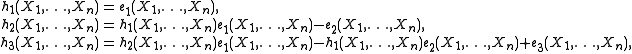
and so on, that allows to recursively express the successive complete homogeneous symmetric polynomials in terms of the elementary symmetric polynomials; the latter gives a set of equations
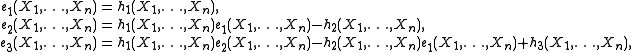
and so forth, that allows doing the inverse. The first n elementary and complete homogeneous symmetric polynomials play perfectly similar roles in these relations, even though the former polynomials then become zero, whereas the latter do not. This phenomenon can be understood in the setting of the ring of symmetric functions. It has a ring automorphism that interchanges the sequences of the n elementary and first n complete homogeneous symmetric functions.
The set of complete homogeneous symmetric polynomials of degree 1 to n in n variables generates the ring
of symmetric polynomial
s in n variables. More specifically, the ring of symmetric polynomials with integer coefficients equals the integral polynomial ring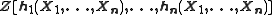 . This can be formulated by saying that
. This can be formulated by saying that 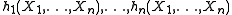 form an algebraic basis of the ring of symmetric polynomials in X1, … Xn with integral coefficients (as is also true for the elementary symmetric polynomials). The same is true with the ring Z of integers replaced by any other commutative ring
form an algebraic basis of the ring of symmetric polynomials in X1, … Xn with integral coefficients (as is also true for the elementary symmetric polynomials). The same is true with the ring Z of integers replaced by any other commutative ring
. These statements follow from analogous statements for the elementary symmetric polynomials, due to the indicated possibility of expressing either kind of symmetric polynomials in terms of the other kind.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic combinatorics
Algebraic combinatorics
Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
and commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s. Every symmetric polynomial can be expressed as a polynomial expression in complete homogeneous symmetric polynomials.
Definition
The complete homogeneous symmetric polynomial of degree k in variables X1, ..., Xn, written hk for k = 0, 1, 2, ..., is the sum of all monomial
variables X1, ..., Xn, written hk for k = 0, 1, 2, ..., is the sum of all monomialMonomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s of total degree k in the variables. Formally,
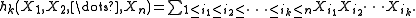
The first few of these polynomials are
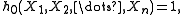
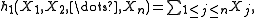
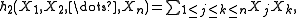

Thus, for each nonnegative integer
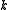 , there exists exactly one complete homogeneous symmetric polynomial of degree
, there exists exactly one complete homogeneous symmetric polynomial of degree 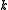 in
in  variables.
variables.The polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
formed by taking all integral linear combinations of products of the complete homogeneous symmetric polynomials is a commutative ring.
Examples
The following lists the basic (as explained below) complete homogeneous symmetric polynomials for the first three positive values of n.
basic (as explained below) complete homogeneous symmetric polynomials for the first three positive values of n.For n = 1:

For n = 2:
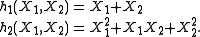
For n = 3:
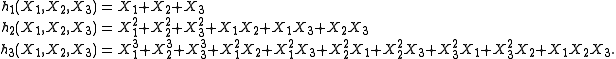
Properties
The complete homogeneous symmetric polynomials are characterized by the following identity of formal power series in t: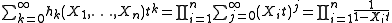
(this is called the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
, or generating series, for the complete homogeneous symmetric polynomials).
Here each fraction in the final expression is the usual way to represent the formal geometric series that is a factor in the middle expression. The identity can be justified by considering how the product of those geometric series is formed: each term of the product is obtained by multiplying one term chosen from each geometric series, and every monomial in the variables Xi is obtained for exactly one such choice of terms, and comes multiplied by a power of t equal to the degree of the monomial.
There is a fundamental relation between the elementary symmetric polynomials and the complete homogeneous ones:
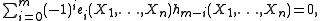
which is valid for all m > 0, and any number of variables n. The easiest way to see that it holds is from an identity of formal power series in t for the elementary symmetric polynomials, analogous to the one given above for the complete homogeneous ones:
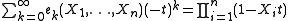
(this is actually an identity of polynomials in t, because after en(X1,…Xn) the elementary symmetric polynomials become zero). Multiplying this by the generating function for the complete homogeneous symmetric polynomials, one obtains the constant series 1, and the relation between the elementary and complete homogeneous polynomials follows from comparing coefficients of tm. A somewhat more direct way to understand that relation, is to consider the contributions in the summation involving a fixed monomial Xα of degree m. For any subset S of the variables appearing with nonzero exponent in the monomial, there is a contribution involving the product XS of those variables as term from es(X1,…,Xn), where s = #S, and the monomial Xα / XS from hm−s(X1,…,Xn); this contribution has coefficient (−1)s. The relation then follows from the fact that
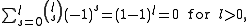
by the binomial formula, where l ≤ m denotes the number of distinct variables occurring (with nonzero exponent) in Xα.
Since e0(X1, …, Xn) and h0(X1, …, Xn) are both equal to 1, one can isolate from the relation either the first or the last terms of the summation. The former gives a sequence of equations
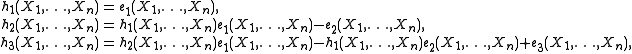
and so on, that allows to recursively express the successive complete homogeneous symmetric polynomials in terms of the elementary symmetric polynomials; the latter gives a set of equations
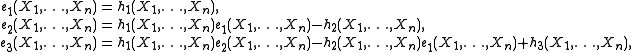
and so forth, that allows doing the inverse. The first n elementary and complete homogeneous symmetric polynomials play perfectly similar roles in these relations, even though the former polynomials then become zero, whereas the latter do not. This phenomenon can be understood in the setting of the ring of symmetric functions. It has a ring automorphism that interchanges the sequences of the n elementary and first n complete homogeneous symmetric functions.
The set of complete homogeneous symmetric polynomials of degree 1 to n in n variables generates the ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
of symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s in n variables. More specifically, the ring of symmetric polynomials with integer coefficients equals the integral polynomial ring
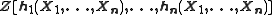 . This can be formulated by saying that
. This can be formulated by saying that 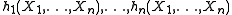 form an algebraic basis of the ring of symmetric polynomials in X1, … Xn with integral coefficients (as is also true for the elementary symmetric polynomials). The same is true with the ring Z of integers replaced by any other commutative ring
form an algebraic basis of the ring of symmetric polynomials in X1, … Xn with integral coefficients (as is also true for the elementary symmetric polynomials). The same is true with the ring Z of integers replaced by any other commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. These statements follow from analogous statements for the elementary symmetric polynomials, due to the indicated possibility of expressing either kind of symmetric polynomials in terms of the other kind.
See also
- Symmetric polynomialSymmetric polynomialIn mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
- Elementary symmetric polynomialElementary symmetric polynomialIn mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
- Newton's identitiesNewton's identitiesIn mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
- Symmetric functionSymmetric functionIn algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
- Representation theoryRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...

