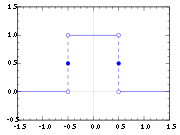
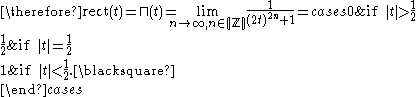The rectangular function (also known as the rectangle

Rectangle

In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...

 function, rect function, Pi function, gate function, unit pulse, or the normalized boxcar function

Boxcar function

In mathematics, a boxcar function is any function which is zero over the entirereal line except for a single interval where it is equal to a constant, A; it is a simple step function...

) is defined as:


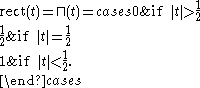
Alternate definitions of the function define 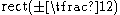to be 0, 1, or undefined.

Relation to the Boxcar Function

The rectangular function is a special case of the more general boxcar function

Boxcar function

In mathematics, a boxcar function is any function which is zero over the entirereal line except for a single interval where it is equal to a constant, A; it is a simple step function...

:


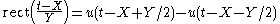
Where the function is centred at X and has duration Y.

Fourier transform of the rectangular function

The unitary Fourier transforms of the rectangular function are: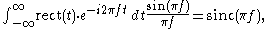


and:


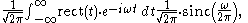
where 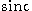 is the normalized form.

Note that as long as the definition of the pulse function is only motivated by the time-domain experience of it, there is no reason to believe that the oscillatory interpretation (i.e. the Fourier transform function) should be intuitive, or directly understood by humans. However, some aspects of the theoretical result may be understood intuitively, such as the infinite bandwidth requirement incurred by the indefinitely-sharp edges in the time-domain definition.

Relation to the Triangular Function

We can define the triangular function as the convolution

Convolution

In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...

 of two rectangular functions:

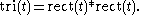
Use in probability

Viewing the rectangular function as a probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

, it is a special case of the continuous uniform distribution

Uniform distribution (continuous)

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

 with 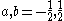. The characteristic function

Characteristic function (probability theory)

In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...

 is:


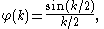
and its moment generating function is:


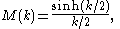
where 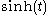is the hyperbolic sine function.

Rational approximation

The pulse function may also be expressed as a limit of a rational function

Rational function

In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...

:

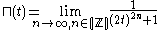
Demonstration of validity

First, we consider the case where . Notice that the term is always positive for integer . However, 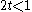and hence (2t)^{2n} approaches zero for large .

It follows that:

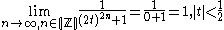
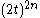Second, we consider the case where . Notice that the term is always positive for integer . However, 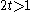and hence (2t)^{2n} grows very large for large .

It follows that:

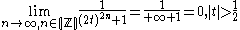
Third, we consider the case where 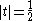. We may simply substitute in our equation: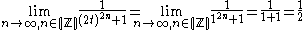


We see that it satisfies the definition of the pulse function.