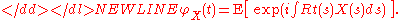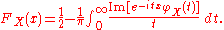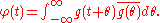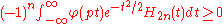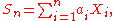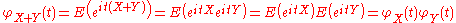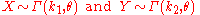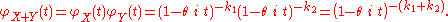Characteristic function (probability theory)

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

and statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, the characteristic function of any random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

completely defines its probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

s or cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

s. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables.

In addition to univariate distributions, characteristic functions can be defined for vector- or matrix-valued random variables, and can even be extended to more generic cases.

The characteristic function always exists when treated as a function of a real-valued argument, unlike the moment-generating function

Moment-generating function

In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...

. There are relations between the behavior of the characteristic function of a distribution and properties of the distribution, such as the existence of moments and the existence of a density function.

Introduction

The characteristic function provides an alternative way for describing a random variable

Random variable

. Similarly to the cumulative distribution function

Cumulative distribution function

F_X(x) = \operatorname{E}[\,\mathbf{1}_{\{X\leq x\}}\,] (where 1{X ≤ x} is the indicator function — it is equal to 1 when , and zero otherwise)
which completely determines behavior and properties of the probability distribution of the random variable X, the characteristic function

also completely determines behavior and properties of the probability distribution of the random variable X. The two approaches are equivalent in the sense that knowing one of the functions it is always possible to find the other, yet they both provide different insight for understanding the features of the random variable. However, in particular cases, there can be differences in whether these functions can be represented as expressions involving simple standard functions.

If a random variable admits a density function

Probability density function

, then the characteristic function is its dual

Duality (mathematics)

In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...

, in the sense that each of them is a Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

of the other. If a random variable has a moment-generating function

Moment-generating function

, then the domain of the characteristic function can be extended to the complex plane, and

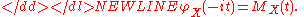
Note however that the characteristic function of a distribution always exists, even when the probability density function

Probability density function

or moment-generating function

Moment-generating function

do not.

The characteristic function approach is particularly useful in analysis of linear combinations of independent random variables. Another important application is to the theory of the decomposability

Indecomposable distribution

In probability theory, an indecomposable distribution is a probability distribution that cannot be represented as the distribution of the sum of two or more non-constant independent random variables: Z ≠ X + Y. If it can be so expressed, it is decomposable:...

of random variables.

Definition

For a scalar random variable X the characteristic function is defined as the expected value

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

of e^itX, where i is the imaginary unit

Imaginary unit

In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...

, and is the argument of the characteristic function:

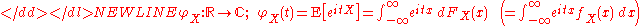
Here F_X is the cumulative distribution function

Cumulative distribution function

of X, and the integral is of the Riemann–Stieltjes kind. If random variable X has a probability density function

Probability density function

ƒ_X, then the characteristic function is its Fourier transform

Fourier transform

, and the last formula in parentheses is valid.

It should be noted though, that this convention for the constants appearing in the definition of the characteristic function differs from the usual convention for the Fourier transform. For example some authors define , which is essentially a change of parameter. Other notation may be encountered in the literature:

\scriptstyle\hat p

as the characteristic function for a probability measure p, or

\scriptstyle\hat f

as the characteristic function corresponding to a density ƒ.

The notion of characteristic functions generalizes to multivariate random variables and more complicated random element

Random element

In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...

s. The argument of the characteristic function will always belong to the continuous dual of the space where random variable X takes values. For common cases such definitions are listed below:

If X is a k-dimensional random vector, then for

If X is a k×p-dimensional random matrix
Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...

, then for

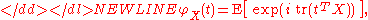
If X is a complex random variable, then for

If X is a k-dimensional complex random vector, then for

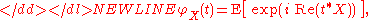
If X(s) is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

, then for all functions t(s) such that the integral ∫_Rt(s)X(s)ds converges for almost all realizations of X

Here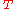

denotes matrix transpose

Transpose

In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...

, tr(·) — the matrix trace

Trace (linear algebra)

In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...

operator, Re(·) is the real part of a complex number, z denotes complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

, and * is conjugate transpose

Conjugate transpose

In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...

(that is ).

Examples

Distribution	Characteristic function φ(t)
Degenerate δ_a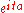
Bernoulli Bern(p)
Binomial B(n, p)
Negative binomial Negative binomial distribution In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur... NB(r, p)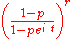
Poisson Poisson distribution In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since... Pois(λ)
Uniform Uniform distribution (continuous) In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by... U(a, b)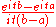
Laplace L(μ, b)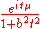
Normal N(μ, σ²)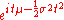
Chi-squared χ²_k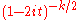
Cauchy Cauchy distribution The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner... Cauchy(μ, θ)

|-
| Gamma Γ(k, θ)
|

|-
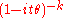
| Exponential

Exponential distribution

In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...

Exp(λ)
|

|-
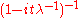
| Multivariate normal N(μ, Σ)
|

|-
|}
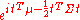
Oberhettinger (1973) provides extensive tables of characteristic functions.

Properties

The characteristic function of a random variable always exists, since it is an integral of a bounded continuous function over a space whose measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

is finite.
A characteristic function is uniformly continuous
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...

on the entire space
It is non-vanishing in a region around zero: .
It is bounded: .
It is Hermitian: . In particular, the characteristic function of a symmetric (around the origin) random variable is real-valued and even.
There is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

between distribution functions
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

and characteristic functions. That is, for any two random variables X₁, X₂

If a random variable X has moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...

up to k-th order, then the characteristic function φ_X is k times continuously differentiable on the entire real line. In this case

If a characteristic function φ_X has a k-th derivative at zero, then the random variable X has all moments up to k if k is even, but only up to if k is odd.

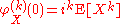
If X₁, …, X_n are independent random variables, and a₁, …, a_n are some constants, then the characteristic function of the linear combination of X_i's is

One specific case would be the sum of two independent random variables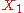

and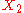

in which case one would have

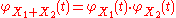The tail behavior of the characteristic function determines the smoothness
Smoothness (probability theory)
In probability theory and statistics, smoothness of a density function is a measure which determines how many times the density function can be differentiated, or equivalently the limiting behavior of distribution’s characteristic function....

of the corresponding density function.

Continuity

The bijection stated above between probability distributions and characteristic functions is continuous. That is, whenever a sequence of distribution functions } converges (weakly) to some distribution F(x), the corresponding sequence of characteristic functions } will also converge, and the limit φ(t) will correspond to the characteristic function of law F. More formally, this is stated as

Lévy’s continuity theorem: A sequence } of n-variate random variables converges in distribution to random variable X if and only if the sequence } converges pointwise to a function φ which is continuous at the origin. Then φ is the characteristic function of X.

This theorem is frequently used to prove the law of large numbers, and the central limit theorem.

Inversion formulas

Since there is a one-to-one correspondence

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

between cumulative distribution functions and characteristic functions, it is always possible to find one of these functions if we know the other one. The formula in definition of characteristic function allows us to compute φ when we know the distribution function F (or density ƒ). If, on the other hand, we know the characteristic function φ and want to find the corresponding distribution function, then one of the following inversion theorems can be used.

Theorem. If characteristic function φ_X is integrable, then F_X is absolutely continuous, and therefore X has the probability density function

Probability density function

given by

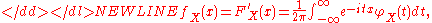when X is scalar;
in multivariate case the pdf is understood as the Radon–Nikodym derivative of the distribution μ_X with respect to the Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

λ:

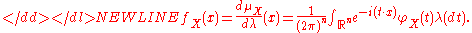
Theorem (Lévy). If φ_X is characteristic function of distribution function F_X, two points a<b are such that } is a continuity set

Continuity set

In measure theory, a continuity set of a measure μ is any Borel set B such that |\mu| = 0\,. The class of all continuity sets for given measure μ forms a ring....

of μ_X (in the univariate case this condition is equivalent to continuity of F_X at points a and b), then

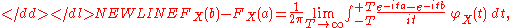if X is scalar

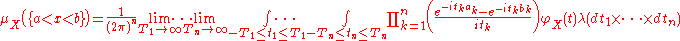, if X is a vector random variable.

Theorem. If a is (possibly) an atom of X (in the univariate case this means a point of discontinuity of F_X) then

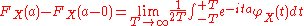, when X is a scalar random variable

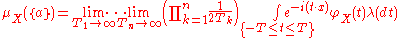, when X is a vector random variable.

Theorem (Gil-Pelaez). For a univariate random variable X, if x is a continuity point of F_X then

Inversion formula for multivariate distributions are available.

Criteria for characteristic functions

It is well-known that any non-decreasing càdlàg

Càdlàg

In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...

function F with limits F(−∞) = 0, F(+∞) = 1 corresponds to a cumulative distribution function

Cumulative distribution function

of some random variable.

There is also interest in finding similar simple criteria for when a given function φ could be the characteristic function of some random variable. The central result here is Bochner’s theorem

Bochner's theorem

In mathematics, Bochner's theorem characterizes the Fourier transform of a positive finite Borel measure on the real line.- Background :...

, although its usefulness is limited because the main condition of the theorem, non-negative definiteness, is very hard to verify. Other theorems also exist, such as Khinchine’s, Mathias’s, or Cramér’s, although their application is just as difficult. Pólya’s theorem, on the other hand, provides a very simple convexity condition which is sufficient but not necessary. Characteristic functions which satisfy this condition are called Pólya-type.

Bochner’s theorem
Bochner's theorem
In mathematics, Bochner's theorem characterizes the Fourier transform of a positive finite Borel measure on the real line.- Background :...

. An arbitrary function is the characteristic function of some random variable if and only if φ is positive definite, continuous at the origin, and if φ(0) = 1.

Khinchine’s criterion. An absolutely continuous complex-valued function φ equal to 1 at the origin is a characteristic function if and only if it admits the representation

Mathias’ theorem. A real, even, continuous, absolutely integrable function φ equal to 1 at the origin is a characteristic function if and only if

for n = 0,1,2,…, and all p > 0. Here H_2n denotes the Hermite polynomial
Hermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...

of degree 2n.

Pólya’s theorem. If φ is a real-valued continuous function which satisfies the conditions
1. φ(0) = 1,
2. φ is even
  Even and odd functions
  In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
  
  ,
3. φ is convex
  Convex function
  In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
  
  for t>0,
4. φ(∞) = 0,
then φ(t) is the characteristic function of an absolutely continuous symmetric distribution.

A convex linear combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....

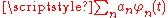(with 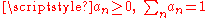) of a finite or a countable number of characteristic functions is also a characteristic function.

The product of a finite number of characteristic functions is also a characteristic function. The same holds for an infinite product provided that it converges to a function continuous at the origin.

If φ is a characteristic function and α is a real number, then φ, Re[φ], |φ|², and φ(αt) are also characteristic functions.

Uses

Because of the continuity theorem

Lévy continuity theorem

In probability theory, the Lévy’s continuity theorem, named after the French mathematician Paul Lévy, connects convergence in distribution of the sequence of random variables with pointwise convergence of their characteristic functions...

, characteristic functions are used in the most frequently seen proof of the central limit theorem

Central limit theorem

In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...

. The main trick involved in making calculations with a characteristic function is recognizing the function as the characteristic function of a particular distribution.

Basic manipulations of distributions

Characteristic functions are particularly useful for dealing with linear functions of independent

Statistical independence

In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...

random variables. For example, if X₁, X₂, ..., X_n is a sequence of independent (and not necessarily identically distributed) random variables, and

where the a_i are constants, then the characteristic function for S_n is given by

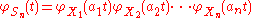
In particular, . To see this, write out the definition of characteristic function:

Observe that the independence of X and Y is required to establish the equality of the third and fourth expressions.

Another special case of interest is when and then S_n is the sample mean. In this case, writing X for the mean,

Moments

Characteristic functions can also be used to find moments

Moment (mathematics)

In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...

of a random variable. Provided that the n^th moment exists, characteristic function can be differentiated n times and

For example, suppose X has a standard Cauchy distribution

Cauchy distribution

The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...

. Then . See how this is not differentiable at t = 0, showing that the Cauchy distribution has no expectation

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

. Also see that the characteristic function of the sample mean X of n independent

Statistical independence

In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...

observations has characteristic function , using the result from the previous section. This is the characteristic function of the standard Cauchy distribution: thus, the sample mean has the same distribution as the population itself.

The logarithm of a characteristic function is a cumulant generating function, which is useful for finding cumulant

Cumulant

In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...

s; note that some instead define the cumulant generating function as the logarithm of the moment-generating function

Moment-generating function

, and call the logarithm of the characteristic function the second cumulant generating function.

Data analysis

Characteristic functions can be used as part of procedures for fitting probability distributions to samples of data. Cases where this provides a practicable option compared to other possibilities include fitting the stable distribution since closed form expressions for the density are not available which makes implementation of maximum likelihood

Maximum likelihood

In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....

estimation difficult. Estimation procedures are available which match the theoretical characteristic function to the empirical characteristic function, calculated from the data. Paulson et al. (1975) and Heathcote (1977) provide some theoretical background for such an estimation procedure. In addition, Yu (2004) describes applications of empirical characteristic functions to fit time series

Time series

In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...

models where likelihood procedures are impractical.

Example

The Gamma distribution with scale parameter θ and a shape parameter k has the characteristic function

Now suppose that we have

with X and Y independent from each other, and we wish to know what the distribution of X + Y is. The characteristic functions are

which by independence and the basic properties of characteristic function leads to

This is the characteristic function of the gamma distribution scale parameter θ and shape parameter k₁ + k₂, and we therefore conclude

The result can be expanded to n independent gamma distributed random variables with the same scale parameter and we get

Entire characteristic functions

As defined above, the argument of the characteristic function is treated as a real number: however, certain aspects of the theory of characteristic functions are advanced by extending the definition into the complex plane by analytical continuation

Analytic continuation

In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...

, in cases where this is possible.

Related concepts

Related concepts include the moment-generating function

Moment-generating function

and the probability-generating function

Probability-generating function

In probability theory, the probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable...

. The characteristic function exists for all probability distributions. However this is not the case for moment generating function.

The characteristic function is closely related to the Fourier transform

Fourier transform

:
the characteristic function of a probability density function p(x) is the complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

of the continuous Fourier transform

Continuous Fourier transform

The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...

of p(x) (according to the usual convention; see continuous Fourier transform – other conventions).

where P(t) denotes the continuous Fourier transform

Continuous Fourier transform

of the probability density function p(x).
Likewise, p(x) may be recovered from φ_X(t) through the inverse Fourier transform:

Indeed, even when the random variable does not have a density, the characteristic function may be seen as the Fourier transform of the measure corresponding to the random variable.

Introduction

Definition

Examples

Properties

Continuity

Inversion formulas

Criteria for characteristic functions

Uses

Basic manipulations of distributions

Moments

Data analysis

Example

Entire characteristic functions

Related concepts

See also