
Real analytic Eisenstein series
Encyclopedia
In mathematics
, the simplest real analytic Eisenstein series is a special function of two variables. It is used in the representation theory
of SL(2,R) and in analytic number theory
. It is closely related to the Epstein zeta function.
There are many generalizations associated to more complicated groups.
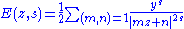
for Re(s) > 1, and by analytic continuation for other values of the complex number s. The sum is over all pairs of coprime integers.
Warning: there are several other slightly different definitions. Some authors omit the factor of ½, and some sum over all pairs of integers that are not both zero; which changes the function by a factor of ζ(2s).
of the Laplace operator
on H with the eigenvalue s(s-1). In other words, it satisfies the elliptic partial differential equation
The function E(z, s) is invariant under the action of SL(2,Z) on z in the upper half plane by fractional linear transformations. Together with the previous property, this means that the Eisenstein series is a Maass form, a real-analytic analogue of a classical elliptic modular function.
Warning: E(z, s) is not a square-integrable function of z with respect to the invariant Riemannian metric on H.
to a meromorphic function of s on the entire complex plane, with a unique pole of residue 3/π at s = 1 (for all z in H). The constant term of the pole at s = 1 is described by the Kronecker limit formula
.
The modified function
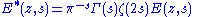
satisfies the functional equation
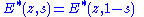
analogous to the functional equation for the Riemann zeta function ζ(s).
Scalar product of two different Eisenstein series E(z, s) and E(z, t) is given by the Maass-Selberg relations.
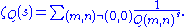
It is essentially a special case of the real analytic Eisenstein series for a special value of z, since
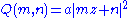
for
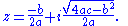
This zeta function was named after Paul Epstein
.
of SL(2,R). Selberg
described generalizations to other discrete subgroups Γ of SL(2,R), and used these to study the representation of SL(2,R) on L2(SL(2,R)/Γ). Langlands
extended Selberg's work to higher dimensional groups; his notoriously difficult proofs were later simplified by Joseph Bernstein
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the simplest real analytic Eisenstein series is a special function of two variables. It is used in the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of SL(2,R) and in analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
. It is closely related to the Epstein zeta function.
There are many generalizations associated to more complicated groups.
Definition
The Eisenstein series E(z, s) for z = x + iy in the upper half-plane is defined by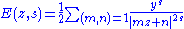
for Re(s) > 1, and by analytic continuation for other values of the complex number s. The sum is over all pairs of coprime integers.
Warning: there are several other slightly different definitions. Some authors omit the factor of ½, and some sum over all pairs of integers that are not both zero; which changes the function by a factor of ζ(2s).
As a function on z
Viewed as a function of z, E(z,s) is a real-analytic eigenfunctionEigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
on H with the eigenvalue s(s-1). In other words, it satisfies the elliptic partial differential equation
-
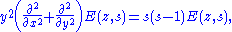 where
where 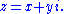
The function E(z, s) is invariant under the action of SL(2,Z) on z in the upper half plane by fractional linear transformations. Together with the previous property, this means that the Eisenstein series is a Maass form, a real-analytic analogue of a classical elliptic modular function.
Warning: E(z, s) is not a square-integrable function of z with respect to the invariant Riemannian metric on H.
As a function on s
The Eisenstein series converges for Re(s)>1, but can be analytically continuedAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to a meromorphic function of s on the entire complex plane, with a unique pole of residue 3/π at s = 1 (for all z in H). The constant term of the pole at s = 1 is described by the Kronecker limit formula
Kronecker limit formula
In mathematics, the classical Kronecker limit formula describes the constant term at s = 1 of a real analytic Eisenstein series in terms of the Dedekind eta function. There are many generalizations of it to more complicated Eisenstein series...
.
The modified function
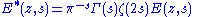
satisfies the functional equation
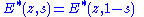
analogous to the functional equation for the Riemann zeta function ζ(s).
Scalar product of two different Eisenstein series E(z, s) and E(z, t) is given by the Maass-Selberg relations.
Epstein zeta function
The Epstein zeta function ζQ(s) for a positive definite integral quadratic form Q(m, n) = cm2 + bmn +an2 is defined by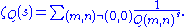
It is essentially a special case of the real analytic Eisenstein series for a special value of z, since
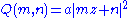
for
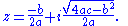
This zeta function was named after Paul Epstein
Paul Epstein
Paul Epstein was a German mathematician. He was known for his contributions to number theory, in particular the Epstein zeta function....
.
Generalizations
The real analytic Eisenstein series E(z, s) is really the Eisenstein series associated to the discrete subgroup SL(2,Z)Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
of SL(2,R). Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
described generalizations to other discrete subgroups Γ of SL(2,R), and used these to study the representation of SL(2,R) on L2(SL(2,R)/Γ). Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
extended Selberg's work to higher dimensional groups; his notoriously difficult proofs were later simplified by Joseph Bernstein
Joseph Bernstein
Joseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
.

