
Rate function
Encyclopedia
In mathematics
— specifically, in large deviations theory
— a rate function is a function used to quantify the probabilities
of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle. In some sense, the large deviation principle is an analogue of weak convergence of probability measures
, but one which takes account of how well the rare events behave.
A rate function is also called a Cramér function, after the Swedish statistician Harald Cramér
.
function I : X → [0, +∞] defined on a Hausdorff
topological space
X is said to be a rate function if it is not identically +∞ and is lower semi-continuous, i.e. all the sub-level sets
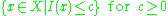
are closed
in X. If, furthermore, they are compact
, then I is said to be a good rate function.
A family of probability measure
s (μδ)δ>0 on X is said to satisfy the large deviation principle with rate function I : X → [0, +∞) (and rate 1 ⁄ δ) if, for every closed set F ⊆ X and every open set
G ⊆ X,
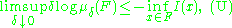
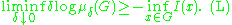
If the upper bound (U) holds only for compact (instead of closed) sets F, then (μδ)δ>0 is said to satisfy the weak large deviation principle (with rate 1 ⁄ δ and weak rate function I).
G ⊆ X,
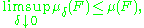

There is some variation in the nomenclature used in the literature: for example, den Hollander (2000) uses simply "rate function" where this article — following Dembo & Zeitouni (1998) — uses "good rate function", and "weak rate function" where this article uses "rate function". Fortunately, regardless of the nomenclature used for rate functions, examination of whether the upper bound inequality (U) is supposed to hold for closed or compact sets tells one whether the large deviation principle in use is strong or weak.
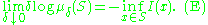
Unfortunately, the equality (E) is far too restrictive, since many interesting examples satisfy (U) and (L) but not (E). For example, the measure μδ might be non-atomic
for all δ, so the equality (E) could hold for S = {x} only if I were identically +∞, which is not permitted in the definition. However, the inequalities (U) and (L) do imply the equality (E) for so-called I-continuous sets S ⊆ X, those for which
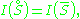
where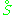 and
and  denote the interior
denote the interior
and closure
of S in X respectively. In many examples, many sets/events of interest are I-continuous. For example, if I is a continuous function
, then all sets S such that
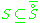
are I-continuous; all open sets, for example, satisfy this containment.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in large deviations theory
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
— a rate function is a function used to quantify the probabilities
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle. In some sense, the large deviation principle is an analogue of weak convergence of probability measures
Convergence of measures
In mathematics, more specifically measure theory, there are various notions of the convergence of measures. Three of the most common notions of convergence are described below.-Total variation convergence of measures:...
, but one which takes account of how well the rare events behave.
A rate function is also called a Cramér function, after the Swedish statistician Harald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
.
Definitions
An extended real-valuedExtended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
function I : X → [0, +∞] defined on a Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is said to be a rate function if it is not identically +∞ and is lower semi-continuous, i.e. all the sub-level sets
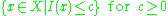
are closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in X. If, furthermore, they are compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, then I is said to be a good rate function.
A family of probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s (μδ)δ>0 on X is said to satisfy the large deviation principle with rate function I : X → [0, +∞) (and rate 1 ⁄ δ) if, for every closed set F ⊆ X and every open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
G ⊆ X,
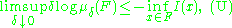
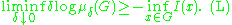
If the upper bound (U) holds only for compact (instead of closed) sets F, then (μδ)δ>0 is said to satisfy the weak large deviation principle (with rate 1 ⁄ δ and weak rate function I).
Remarks
The role of the open and closed sets in the large deviation principle is similar to their role in the weak convergence of probability measures: recall that (μδ)δ>0 is said to converge weakly to μ if, for every closed set F ⊆ X and every open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
G ⊆ X,
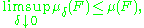

There is some variation in the nomenclature used in the literature: for example, den Hollander (2000) uses simply "rate function" where this article — following Dembo & Zeitouni (1998) — uses "good rate function", and "weak rate function" where this article uses "rate function". Fortunately, regardless of the nomenclature used for rate functions, examination of whether the upper bound inequality (U) is supposed to hold for closed or compact sets tells one whether the large deviation principle in use is strong or weak.
Uniqueness
A natural question to ask, given the somewhat abstract setting of the general framework above, is whether the rate function is unique. This turns out to be the case: given a sequence of probability measures (μδ)δ>0 on X satisfying the large deviation principle for two rate functions I and J, it follows that I(x) = J(x) for all x ∈ X.Exponential tightness
It is possible to convert a weak large deviation principle into a strong one if the measures converge sufficiently quickly. If the upper bound holds for compact sets F and the sequence of measures (μδ)δ>0 is exponentially tight, then the upper bound also holds for closed sets F. In other words, exponential tightness enables one to convert a weak large deviation principle into a strong one.Continuity
Naïvely, one might try to replace the two inequalities (U) and (L) by the single requirement that, for all Borel sets S ⊆ X,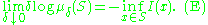
Unfortunately, the equality (E) is far too restrictive, since many interesting examples satisfy (U) and (L) but not (E). For example, the measure μδ might be non-atomic
Atom (measure theory)
In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure...
for all δ, so the equality (E) could hold for S = {x} only if I were identically +∞, which is not permitted in the definition. However, the inequalities (U) and (L) do imply the equality (E) for so-called I-continuous sets S ⊆ X, those for which
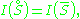
where
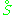 and
and  denote the interior
denote the interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
and closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of S in X respectively. In many examples, many sets/events of interest are I-continuous. For example, if I is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, then all sets S such that
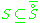
are I-continuous; all open sets, for example, satisfy this containment.
Transformation of large deviation principles
Given a large deviation principle on one space, it is often of interest to be able to construct a large deviation principle on another space. There are several results in this area:- the contraction principleContraction principle (large deviations theory)In mathematics — specifically, in large deviations theory — the contraction principle is a theorem that states how a large deviation principle on one space "pushes forward" to a large deviation principle on another space via a continuous function.-Statement of the theorem:Let X and Y be...
tells one how a large deviation principle on one space "pushes forwardPush forwardSuppose that φ : M → N is a smooth map between smooth manifolds; then the differential of φ at a point x is, in some sense, the best linear approximation of φ near x. It can be viewed as a generalization of the total derivative of ordinary calculus...
" to a large deviation principle on another space via a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
;
- the Dawson-Gärtner theoremDawson-Gärtner theoremIn mathematics, the Dawson–Gärtner theorem is a result in large deviations theory. Heuristically speaking, the Dawson–Gärtner theorem allows one to transport a large deviation principle on a “smaller” topological space to a “larger” one....
tells one how a sequence of large deviation principles on a sequence of spaces passes to the projective limit.
- the tilted large deviation principleTilted large deviation principleIn mathematics — specifically, in large deviations theory — the tilted large deviation principle is a result that allows one to generate a new large deviation principle from an old one by "tilting", i.e. integration against an exponential functional...
gives a large deviation principle for integrals of exponential functionalFunctionalGenerally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
s.
- exponentially equivalent measuresExponentially equivalent measuresIn mathematics, the notion of exponential equivalence of measures is a concept that describes how two sequences or families of probability measures are “the same” from the point of view of large deviations theory.-Definition:...
have the same large deviation principles.

