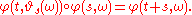Random dynamical system
Encyclopedia
In mathematics
, a random dynamical system is a measure-theoretic formulation of a dynamical system
with an element of "randomness", such as the dynamics of solutions to a stochastic differential equation
. It consists of a base flow, the "noise", and a cocycle
dynamical system on the "physical" phase space
.
 be a
be a 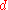 -dimensional vector field
-dimensional vector field
, and let . Suppose that the solution
. Suppose that the solution  to the stochastic differential equation
to the stochastic differential equation

exists for all positive time and some (small) interval of negative time dependent upon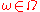 , where
, where  denotes a
denotes a 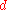 -dimensional Wiener process
-dimensional Wiener process
(Brownian motion
). Implicitly, this statement uses the classical Wiener
probability space

In this context, the Wiener process is the coordinate process.
Now define a flow map or (solution operator) by
by

(whenever the right hand side is well-defined
). Then (or, more precisely, the pair
(or, more precisely, the pair 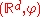 ) is a (local, left-sided) random dynamical system. The process of generating a "flow" from the solution to a stochastic differential equation leads us to study suitably defined "flows" on their own. These "flows" are random dynamical systems.
) is a (local, left-sided) random dynamical system. The process of generating a "flow" from the solution to a stochastic differential equation leads us to study suitably defined "flows" on their own. These "flows" are random dynamical systems.
Let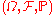 be a probability space
be a probability space
, the noise space. Define the base flow as follows: for each "time"
as follows: for each "time" 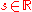 , let
, let 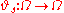 be a measure-preserving measurable function
be a measure-preserving measurable function
:
 for all
for all 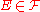 and
and 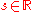 ;
;
Suppose also that
That is, ,
,  , forms a group
, forms a group
of measure-preserving transformation of the noise . For one-sided random dynamical systems, one would consider only positive indices
. For one-sided random dynamical systems, one would consider only positive indices  ; for discrete-time random dynamical systems, one would consider only integer-valued
; for discrete-time random dynamical systems, one would consider only integer-valued  ; in these cases, the maps
; in these cases, the maps 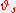 would only form a commutative monoid
would only form a commutative monoid
instead of a group.
While true in most applications, it is not usually part of the formal definition of a random dynamical system to require that the measure-preserving dynamical system
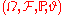 is ergodic.
is ergodic.
Now let be a complete
be a complete
separable metric space
, the phase space. Let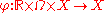 be a
be a  -measurable function such that
-measurable function such that
In the case of random dynamical systems driven by a Wiener process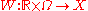 , the base flow
, the base flow 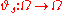 would be given by
would be given by
 .
.
This can be read as saying that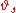 "starts the noise at time
"starts the noise at time  instead of time 0". Thus, the cocycle property can be read as saying that evolving the initial condition
instead of time 0". Thus, the cocycle property can be read as saying that evolving the initial condition  with some noise
with some noise  for
for  seconds and then through
seconds and then through  seconds with the same noise (as started from the
seconds with the same noise (as started from the  seconds mark) gives the same result as evolving
seconds mark) gives the same result as evolving  through
through  seconds with that same noise.
seconds with that same noise.
for a random dynamical system is not as straightforward to define as in the deterministic case. For technical reasons, it is necessary to "rewind time", as in the definition of a pullback attractor
. Moreover, the attractor is dependent upon the realisation of the noise.
of the noise.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a random dynamical system is a measure-theoretic formulation of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
with an element of "randomness", such as the dynamics of solutions to a stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
. It consists of a base flow, the "noise", and a cocycle
Oseledec theorem
In mathematics, the multiplicative ergodic theorem, or Oseledets theorem provides the theoretical background for computation of Lyapunov exponents of a nonlinear dynamical system. It was proved by Valery Oseledets in 1965 and reported at the International Mathematical Congress in Moscow in 1966...
dynamical system on the "physical" phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
Motivation: solutions to a stochastic differential equation
Let be a
be a 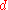 -dimensional vector field
-dimensional vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, and let
 . Suppose that the solution
. Suppose that the solution  to the stochastic differential equation
to the stochastic differential equation
exists for all positive time and some (small) interval of negative time dependent upon
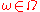 , where
, where  denotes a
denotes a 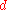 -dimensional Wiener process
-dimensional Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
). Implicitly, this statement uses the classical Wiener
Classical Wiener space
In mathematics, classical Wiener space is the collection of all continuous functions on a given domain , taking values in a metric space . Classical Wiener space is useful in the study of stochastic processes whose sample paths are continuous functions...
probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

In this context, the Wiener process is the coordinate process.
Now define a flow map or (solution operator)
 by
by
(whenever the right hand side is well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
). Then
 (or, more precisely, the pair
(or, more precisely, the pair 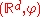 ) is a (local, left-sided) random dynamical system. The process of generating a "flow" from the solution to a stochastic differential equation leads us to study suitably defined "flows" on their own. These "flows" are random dynamical systems.
) is a (local, left-sided) random dynamical system. The process of generating a "flow" from the solution to a stochastic differential equation leads us to study suitably defined "flows" on their own. These "flows" are random dynamical systems.Formal definition
Formally, a random dynamical system consists of a base flow, the "noise", and a cocycle dynamical system on the "physical" phase space. In detail.Let
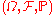 be a probability space
be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, the noise space. Define the base flow
 as follows: for each "time"
as follows: for each "time" 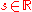 , let
, let 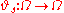 be a measure-preserving measurable function
be a measure-preserving measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
:
 for all
for all 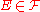 and
and 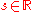 ;
;Suppose also that
-
 , the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
, the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on ;
; - for all
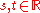 ,
,  .
.
That is,
 ,
,  , forms a group
, forms a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of measure-preserving transformation of the noise
 . For one-sided random dynamical systems, one would consider only positive indices
. For one-sided random dynamical systems, one would consider only positive indices  ; for discrete-time random dynamical systems, one would consider only integer-valued
; for discrete-time random dynamical systems, one would consider only integer-valued  ; in these cases, the maps
; in these cases, the maps 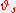 would only form a commutative monoid
would only form a commutative monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
instead of a group.
While true in most applications, it is not usually part of the formal definition of a random dynamical system to require that the measure-preserving dynamical system
Measure-preserving dynamical system
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
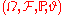 is ergodic.
is ergodic.Now let
 be a complete
be a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
separable metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, the phase space. Let
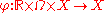 be a
be a  -measurable function such that
-measurable function such that- for all
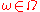 ,
, 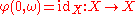 , the identity function on
, the identity function on  ;
; - for (almost) all
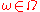 ,
, 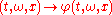 is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in both and
and  ;
; -
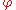 satisfies the (crude) cocycle property: for almost allAlmost allIn mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
satisfies the (crude) cocycle property: for almost allAlmost allIn mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
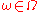 ,
,
In the case of random dynamical systems driven by a Wiener process
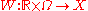 , the base flow
, the base flow 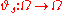 would be given by
would be given by .
.This can be read as saying that
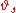 "starts the noise at time
"starts the noise at time  instead of time 0". Thus, the cocycle property can be read as saying that evolving the initial condition
instead of time 0". Thus, the cocycle property can be read as saying that evolving the initial condition  with some noise
with some noise  for
for  seconds and then through
seconds and then through  seconds with the same noise (as started from the
seconds with the same noise (as started from the  seconds mark) gives the same result as evolving
seconds mark) gives the same result as evolving  through
through  seconds with that same noise.
seconds with that same noise.Attractors for random dynamical systems
The notion of an attractorAttractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
for a random dynamical system is not as straightforward to define as in the deterministic case. For technical reasons, it is necessary to "rewind time", as in the definition of a pullback attractor
Pullback attractor
In mathematics, the attractor of a random dynamical system may be loosely thought of as a set to which the system evolves after a long enough time. The basic idea is the same as for a deterministic dynamical system, but requires careful treatment because random dynamical systems are necessarily...
. Moreover, the attractor is dependent upon the realisation
 of the noise.
of the noise.