
Stochastic differential equation
Encyclopedia
A stochastic differential equation (SDE) is a differential equation
in which one or more of the terms is a stochastic process
, thus resulting in a solution which is itself a stochastic process.
SDE are used to model diverse phenomena such as fluctuating stock prices or physical system subject to thermal fluctuations
.
Typically, SDEs incorporate white noise
which can be thought of as the derivative of Brownian motion
(or the Wiener process
); however, it should be mentioned that other types of random fluctuations are possible, such as jump processes
.
. Later Itō
and Stratonovich
put SDEs on more solid mathematical footing.
s. These are sometimes confusingly called "the Langevin equation
" even though there are many possible forms. These consist of an ordinary differential equation containing a deterministic part and an additional random white noise
term. A second form is the Smoluchowski equation
and, more generally, the Fokker-Planck equation
. These are partial differential equations that describe the time evolution of probability distribution function
s. The third form is the stochastic differential equation that is used most frequently in mathematics and quantitative finance (see below). This is similar to the Langevin form, but it is usually written in differential form. SDEs come in two varieties, corresponding to two versions of stochastic calculus.
or the Wiener process
was discovered to be exceptionally complex mathematically. The Wiener process
is nowhere differentiable; thus, it requires its own rules of calculus. There are two dominating versions of stochastic calculus, the Ito stochastic calculus and the Stratonovich stochastic calculus. Each of the two has advantages and disadvantages, and newcomers are often confused whether the one is more appropriate than the other in a given situation. Guidelines exist (e.g. Øksendal, 2003) and conveniently, one can readily convert an Ito SDE to an equivalent Stratonovich SDE and back again. Still, one must be careful which calculus to use when the SDE is initially written down.
Methods include the Euler–Maruyama method, Milstein method
and Runge–Kutta method (SDE)
.
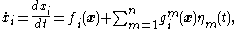
where is the set of unknowns, the
is the set of unknowns, the 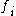 and
and  are arbitrary functions and the
are arbitrary functions and the 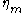 are random functions of time, often referred to as "noise terms". This form is usually usable because there are standard techniques for transforming higher-order equations into several coupled first-order equations by introducing new unknowns. If the
are random functions of time, often referred to as "noise terms". This form is usually usable because there are standard techniques for transforming higher-order equations into several coupled first-order equations by introducing new unknowns. If the 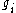 are constants, the system is said to be subject to additive noise, otherwise it is said to be subject to multiplicative noise. This term is somewhat misleading as it has come to mean the general case even though it appears to imply the limited case where :
are constants, the system is said to be subject to additive noise, otherwise it is said to be subject to multiplicative noise. This term is somewhat misleading as it has come to mean the general case even though it appears to imply the limited case where :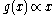 . Additive noise is the simpler of the two cases; in that situation the correct solution can often be found using ordinary calculus
. Additive noise is the simpler of the two cases; in that situation the correct solution can often be found using ordinary calculus
and in particular the ordinary chain rule
of calculus. However, in the case of multiplicative noise, the Langevin equation is not a well-defined entity on its own, and it must be specified whether the Langevin equation should be interpreted as an Ito SDE or a Stratonovich SDE.
In physics, the main method of solution is to find the probability distribution function as a function of time using the equivalent Fokker-Planck equation
(FPE). The Fokker-Planck equation is a deterministic partial differential equation
. It tells how the probability distribution function evolves in time similarly to how the Schrödinger equation
gives the time evolution of the quantum wave function or the diffusion equation gives the time evolution of chemical concentration. Alternatively numerical solutions can be obtained by Monte Carlo
simulation. Other techniques include the path integration
that draws on the analogy between statistical physics and quantum mechanics
(for example, the Fokker-Planck equation can be transformed into the Schrödinger equation
by rescaling a few variables) or by writing down ordinary differential equations for the statistical moments
of the probability distribution function.
. Perhaps, "a Langevin equation" or "the associated Langevin equation" would conform better with common English usage.
(and in many applications of probability theory, for instance mathematical finance
) is slightly different. This notation makes the exotic nature of the random function of time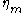 in the physics formulation more explicit. It is also the notation used in publications on numerical methods for solving stochastic differential equations. In strict mathematical terms,
in the physics formulation more explicit. It is also the notation used in publications on numerical methods for solving stochastic differential equations. In strict mathematical terms, 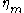 can not be chosen as a usual function, but only as a generalized function
can not be chosen as a usual function, but only as a generalized function
. The mathematical formulation treats this complication with less ambiguity than the physics formulation.
A typical equation is of the form
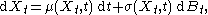
where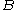 denotes a Wiener process
denotes a Wiener process
(Standard Brownian motion).
This equation should be interpreted as an informal way of expressing the corresponding integral equation
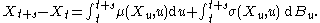
The equation above characterizes the behavior of the continuous time stochastic process
Xt as the sum of an ordinary Lebesgue integral and an Itō integral
. A heuristic
(but very helpful) interpretation of the stochastic differential equation is that in a small time interval of length δ the stochastic process Xt changes its value by an amount that is normally distributed with expectation
μ(Xt, t) δ and variance
σ(Xt, t)² δ and is independent of the past behavior of the process. This is so because the increments of a Wiener process are independent and normally distributed. The function μ is referred to as the drift coefficient, while σ is called the diffusion coefficient. The stochastic process Xt is called a diffusion process
, and is usually a Markov process
.
The formal interpretation of an SDE is given in terms of what constitutes a solution to the SDE. There are two main definitions of a solution to an SDE, a strong solution and a weak solution. Both require the existence of a process Xt that solves the integral equation version of the SDE. The difference between the two lies in the underlying probability space (Ω F, Pr). A weak solution consists of a probability space
and a process that satisfies the integral equation, while a strong solution is a process that satisfies the equation and is defined on a given probability space.
An important example is the equation for geometric Brownian motion
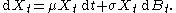
which is the equation for the dynamics of the price of a stock
in the Black Scholes options pricing model of financial mathematics.
There are also more general stochastic differential equations where the coefficients μ and σ depend not only on the present value of the process Xt, but also on previous values of the process and possibly on present or previous values of other processes too. In that case the solution process, X, is not a Markov process, and it is called an Itō process and not a diffusion process. When the coefficients depends only on present and past values of X, the defining equation is called a stochastic delay differential equation.
al Euclidean space
Rn and driven by an m-dimensional Brownian motion B; the proof may be found in Øksendal (2003, §5.2).
Let T > 0, and let
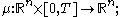
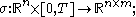
be measurable function
s for which there exist constants C and D such that
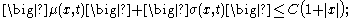
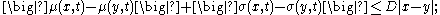
for all t ∈ [0, T] and all x and y ∈ Rn, where
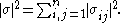
Let Z be a random variable that is independent of the σ-algebra generated by Bs, s ≥ 0, and with finite second moment
:
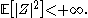
Then the stochastic differential equation/initial value problem

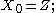
has a Pr-almost surely
unique t-continuous solution (t, ω) |→ Xt(ω) such that X is adapted
to the filtration
FtZ generated by Z and Bs, s ≤ t, and
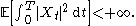
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
in which one or more of the terms is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, thus resulting in a solution which is itself a stochastic process.
SDE are used to model diverse phenomena such as fluctuating stock prices or physical system subject to thermal fluctuations
Thermal fluctuations
In statistical mechanics, thermal fluctuations are random deviations of a system from its equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they disappear altogether as temperature approaches absolute zero.Thermal fluctuations are a...
.
Typically, SDEs incorporate white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
which can be thought of as the derivative of Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
(or the Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
); however, it should be mentioned that other types of random fluctuations are possible, such as jump processes
Jump process
A jump process is a type of stochastic process that has discrete movements, called jumps, rather than small continuous movements.In physics, jump processes result in diffusion...
.
Background
The earliest work on SDEs was done to describe Brownian motion in Einstein's famous paper, and at the same time by Smoluchowski. However, one of the earlier works related to Brownian motion is credited to Bachelier (1900) in his thesis 'Theory of Speculation'. This work was followed upon by LangevinPaul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
. Later Itō
Kiyoshi Ito
was a Japanese mathematician whose work is now called Itō calculus. The basic concept of this calculus is the Itō integral, and among the most important results is Itō's lemma. The Itō calculus facilitates mathematical understanding of random events...
and Stratonovich
Ruslan L. Stratonovich
Ruslan Leont'evich Stratonovich was an outstanding physicist, engineer, and probabilist. Professor Stratonovich was born on May 31, 1930 in Moscow, Russia...
put SDEs on more solid mathematical footing.
Terminology
In physical science, SDEs are usually written as Langevin equationLangevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
s. These are sometimes confusingly called "the Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
" even though there are many possible forms. These consist of an ordinary differential equation containing a deterministic part and an additional random white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
term. A second form is the Smoluchowski equation
Smoluchowski equation
In physics, the diffusion equation with drift term is often called Smoluchowski equation .- The equation :Let w be a density, D a diffusion constant, ζ a friction coefficient,...
and, more generally, the Fokker-Planck equation
Fokker-Planck equation
The Fokker–Planck equation describes the time evolution of the probability density function of the velocity of a particle, and can be generalized to other observables as well.It is named after Adriaan Fokkerand Max Planck...
. These are partial differential equations that describe the time evolution of probability distribution function
Probability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
s. The third form is the stochastic differential equation that is used most frequently in mathematics and quantitative finance (see below). This is similar to the Langevin form, but it is usually written in differential form. SDEs come in two varieties, corresponding to two versions of stochastic calculus.
Stochastic Calculus
Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
or the Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
was discovered to be exceptionally complex mathematically. The Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
is nowhere differentiable; thus, it requires its own rules of calculus. There are two dominating versions of stochastic calculus, the Ito stochastic calculus and the Stratonovich stochastic calculus. Each of the two has advantages and disadvantages, and newcomers are often confused whether the one is more appropriate than the other in a given situation. Guidelines exist (e.g. Øksendal, 2003) and conveniently, one can readily convert an Ito SDE to an equivalent Stratonovich SDE and back again. Still, one must be careful which calculus to use when the SDE is initially written down.
Numerical Solutions
Numerical solution of stochastic differential equations and especially stochastic partial differential equations is a young field relatively speaking. Almost all algorithms that are used for the solution of ordinary differential equations will work very poorly for SDEs, having very poor numerical convergence. A textbook describing many different algorithms is Kloeden & Platen (1995).Methods include the Euler–Maruyama method, Milstein method
Milstein method
In mathematics, the Milstein method, named after Grigori N. Milstein, is a technique for the approximate numerical solution of a stochastic differential equation.Consider the Itō stochastic differential equation...
and Runge–Kutta method (SDE)
Runge–Kutta method (SDE)
In mathematics, the Runge–Kutta method is a technique for the approximate numerical solution of a stochastic differential equation. It is a generalization of the Runge–Kutta method for ordinary differential equations to stochastic differential equations....
.
Use in Physics
In physics, SDEs are typically written in the Langevin form and referred to as "the Langevin equation." For example, a general coupled set of first-order SDEs is often written in the form: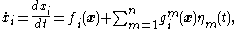
where
 is the set of unknowns, the
is the set of unknowns, the 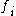 and
and  are arbitrary functions and the
are arbitrary functions and the 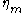 are random functions of time, often referred to as "noise terms". This form is usually usable because there are standard techniques for transforming higher-order equations into several coupled first-order equations by introducing new unknowns. If the
are random functions of time, often referred to as "noise terms". This form is usually usable because there are standard techniques for transforming higher-order equations into several coupled first-order equations by introducing new unknowns. If the 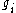 are constants, the system is said to be subject to additive noise, otherwise it is said to be subject to multiplicative noise. This term is somewhat misleading as it has come to mean the general case even though it appears to imply the limited case where :
are constants, the system is said to be subject to additive noise, otherwise it is said to be subject to multiplicative noise. This term is somewhat misleading as it has come to mean the general case even though it appears to imply the limited case where :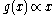 . Additive noise is the simpler of the two cases; in that situation the correct solution can often be found using ordinary calculus
. Additive noise is the simpler of the two cases; in that situation the correct solution can often be found using ordinary calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and in particular the ordinary chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
of calculus. However, in the case of multiplicative noise, the Langevin equation is not a well-defined entity on its own, and it must be specified whether the Langevin equation should be interpreted as an Ito SDE or a Stratonovich SDE.
In physics, the main method of solution is to find the probability distribution function as a function of time using the equivalent Fokker-Planck equation
Fokker-Planck equation
The Fokker–Planck equation describes the time evolution of the probability density function of the velocity of a particle, and can be generalized to other observables as well.It is named after Adriaan Fokkerand Max Planck...
(FPE). The Fokker-Planck equation is a deterministic partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. It tells how the probability distribution function evolves in time similarly to how the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
gives the time evolution of the quantum wave function or the diffusion equation gives the time evolution of chemical concentration. Alternatively numerical solutions can be obtained by Monte Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
simulation. Other techniques include the path integration
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
that draws on the analogy between statistical physics and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(for example, the Fokker-Planck equation can be transformed into the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
by rescaling a few variables) or by writing down ordinary differential equations for the statistical moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the probability distribution function.
Note on "the Langevin equation"
The "the" in "the Langevin equation" is somewhat ungrammatical nomenclature. Each individual physical model has its own Langevin equationLangevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
. Perhaps, "a Langevin equation" or "the associated Langevin equation" would conform better with common English usage.
Use in probability and mathematical finance
The notation used in probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
(and in many applications of probability theory, for instance mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
) is slightly different. This notation makes the exotic nature of the random function of time
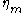 in the physics formulation more explicit. It is also the notation used in publications on numerical methods for solving stochastic differential equations. In strict mathematical terms,
in the physics formulation more explicit. It is also the notation used in publications on numerical methods for solving stochastic differential equations. In strict mathematical terms, 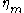 can not be chosen as a usual function, but only as a generalized function
can not be chosen as a usual function, but only as a generalized functionGeneralized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
. The mathematical formulation treats this complication with less ambiguity than the physics formulation.
A typical equation is of the form
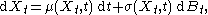
where
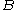 denotes a Wiener process
denotes a Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(Standard Brownian motion).
This equation should be interpreted as an informal way of expressing the corresponding integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
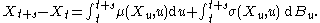
The equation above characterizes the behavior of the continuous time stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
Xt as the sum of an ordinary Lebesgue integral and an Itō integral
Ito calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
. A heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
(but very helpful) interpretation of the stochastic differential equation is that in a small time interval of length δ the stochastic process Xt changes its value by an amount that is normally distributed with expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ(Xt, t) δ and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ(Xt, t)² δ and is independent of the past behavior of the process. This is so because the increments of a Wiener process are independent and normally distributed. The function μ is referred to as the drift coefficient, while σ is called the diffusion coefficient. The stochastic process Xt is called a diffusion process
Diffusion process
In probability theory, a branch of mathematics, a diffusion process is a solution to a stochastic differential equation. It is a continuous-time Markov process with continuous sample paths....
, and is usually a Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
.
The formal interpretation of an SDE is given in terms of what constitutes a solution to the SDE. There are two main definitions of a solution to an SDE, a strong solution and a weak solution. Both require the existence of a process Xt that solves the integral equation version of the SDE. The difference between the two lies in the underlying probability space (Ω F, Pr). A weak solution consists of a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
and a process that satisfies the integral equation, while a strong solution is a process that satisfies the equation and is defined on a given probability space.
An important example is the equation for geometric Brownian motion
Geometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
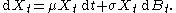
which is the equation for the dynamics of the price of a stock
Stock
The capital stock of a business entity represents the original capital paid into or invested in the business by its founders. It serves as a security for the creditors of a business since it cannot be withdrawn to the detriment of the creditors...
in the Black Scholes options pricing model of financial mathematics.
There are also more general stochastic differential equations where the coefficients μ and σ depend not only on the present value of the process Xt, but also on previous values of the process and possibly on present or previous values of other processes too. In that case the solution process, X, is not a Markov process, and it is called an Itō process and not a diffusion process. When the coefficients depends only on present and past values of X, the defining equation is called a stochastic delay differential equation.
Existence and uniqueness of solutions
As with deterministic ordinary and partial differential equations, it is important to know whether a given SDE has a solution, and whether or not it is unique. The following is a typical existence and uniqueness theorem for Itō SDEs taking values in n-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn and driven by an m-dimensional Brownian motion B; the proof may be found in Øksendal (2003, §5.2).
Let T > 0, and let
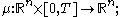
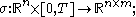
be measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s for which there exist constants C and D such that
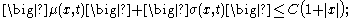
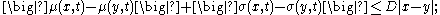
for all t ∈ [0, T] and all x and y ∈ Rn, where
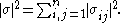
Let Z be a random variable that is independent of the σ-algebra generated by Bs, s ≥ 0, and with finite second moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
:
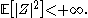
Then the stochastic differential equation/initial value problem

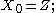
has a Pr-almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
unique t-continuous solution (t, ω) |→ Xt(ω) such that X is adapted
Adapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
to the filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
FtZ generated by Z and Bs, s ≤ t, and
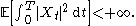
See also
- Langevin dynamicsLangevin dynamicsIn physics, Langevin dynamics is an approach to the mathematical modeling of the dynamics of molecular systems, originally developed by the French physicist Paul Langevin...
- Local volatilityLocal volatilityA local volatility model, in mathematical finance and financial engineering, is one which treats volatility as a function of the current asset level S_t and of time t .-Formulation:...
- Stochastic volatilityStochastic volatilityStochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
- Sethi advertising model
- Stochastic partial differential equations

