
Radiative transfer
Encyclopedia
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption
, emission and scattering
processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media with complex multiple scattering effects numerical methods are required.
The present article is largely focused on the condition of radiative equilibrium
.
.
. If we think of a very small area element in the radiation field, there will be radiation energy flowing through that area element. The flow can be completely characterized by the amount of energy flowing per unit time per unit solid angle
, the direction of the flow, and the wavelength interval being considered (polarization will be ignored for the moment).
In terms of the spectral radiance,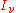 , the energy flowing across an area element of area
, the energy flowing across an area element of area  located at
located at  in time
in time  in the solid angle
in the solid angle  about the direction
about the direction  in the frequency interval
in the frequency interval  to
to 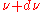 is
is

where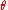 is the angle that the unit direction vector
is the angle that the unit direction vector  makes with a normal to the area element. The units of the spectral radiance are seen to be energy/time/area/solid angle/frequency. In MKS units this would be W·m-2·sr-1·Hz-1 (watts per square-metre-steradian-hertz).
makes with a normal to the area element. The units of the spectral radiance are seen to be energy/time/area/solid angle/frequency. In MKS units this would be W·m-2·sr-1·Hz-1 (watts per square-metre-steradian-hertz).
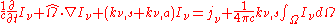
where is the emission coefficient,
is the emission coefficient, 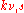 is the scattering cross section, and
is the scattering cross section, and 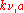 is the absorption cross section.
is the absorption cross section.

where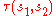 is the optical depth
is the optical depth
of the atmosphere between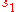 and
and 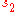 :
:
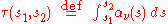
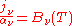
where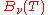 is the black body
is the black body
intensity at temperature T. The solution to the equation of radiative transfer is then:
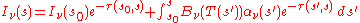
Knowing the temperature profile and the density profile of the atmospheric components will be enough to calculate a solution to the equation of radiative transfer.
. It can be used to obtain the spectral radiance in a plane-parallel atmosphere with isotropic frequency-independent scattering. It assumes that the intensity is a linear function of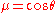 . i.e.
. i.e.
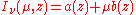
where is the normal direction to the slab atmosphere. Note that expressing angular integrals in terms of
is the normal direction to the slab atmosphere. Note that expressing angular integrals in terms of  simplifies things because
simplifies things because  appears in the Jacobian
appears in the Jacobian
of integrals in spherical coordinates
.
Extracting the first few moments of the spectral radiance with respect to yields
yields


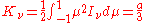
Thus the Eddington approximation is equivalent to setting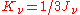 . Higher order versions of the Eddington approximation also exist, and consist of more complicated linear relations of the intensity moments. This extra equation can be used as a closure relation for the truncated system of moments.
. Higher order versions of the Eddington approximation also exist, and consist of more complicated linear relations of the intensity moments. This extra equation can be used as a closure relation for the truncated system of moments.
Note that the first two moments have simple physical meanings.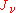 is the isotropic intensity at a point, and
is the isotropic intensity at a point, and 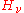 is the flux through that point in the
is the flux through that point in the  direction.
direction.
The radiative transfer through an isotropically scattering atmosphere at local thermal equilibrium is given by
Integrating over all angles yields
Premultiplying by , and then integrating over all angles gives
, and then integrating over all angles gives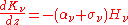
Substituting in the closure relation, and differentiating with respect to allows the two above equations to be combined to form the radiative diffusion equation
allows the two above equations to be combined to form the radiative diffusion equation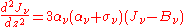
This equation shows how the effective optical depth in scattering-dominated systems may be significantly different from that given by the scattering opacity if the absorptive opacity is small.
Absorption (electromagnetic radiation)
In physics, absorption of electromagnetic radiation is the way by which the energy of a photon is taken up by matter, typically the electrons of an atom. Thus, the electromagnetic energy is transformed to other forms of energy for example, to heat. The absorption of light during wave propagation is...
, emission and scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media with complex multiple scattering effects numerical methods are required.
The present article is largely focused on the condition of radiative equilibrium
Radiative equilibrium
Radiative equilibrium is one of the several requirements for thermodynamic equilibrium, but it can occur in the absence of thermodynamic equilibrium. There are various types of radiative equilibrium, which is itself a kind of dynamic equilibrium....
.
.
Definitions
The fundamental quantity which describes a field of radiation is nowadays called the spectral radiance, traditionally called the specific intensitySpecific radiative intensity
Specific intensity is a fundamental quantity used in theoretical physics that fully describes the field of classical electromagnetic radiation of any kind, including thermal radiation and light. It is a description based on radiometry rather than Maxwellian electromagnetic fields or photon...
. If we think of a very small area element in the radiation field, there will be radiation energy flowing through that area element. The flow can be completely characterized by the amount of energy flowing per unit time per unit solid angle
Solid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
, the direction of the flow, and the wavelength interval being considered (polarization will be ignored for the moment).
In terms of the spectral radiance,
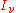 , the energy flowing across an area element of area
, the energy flowing across an area element of area  located at
located at  in time
in time  in the solid angle
in the solid angle  about the direction
about the direction  in the frequency interval
in the frequency interval  to
to 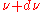 is
is
where
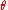 is the angle that the unit direction vector
is the angle that the unit direction vector  makes with a normal to the area element. The units of the spectral radiance are seen to be energy/time/area/solid angle/frequency. In MKS units this would be W·m-2·sr-1·Hz-1 (watts per square-metre-steradian-hertz).
makes with a normal to the area element. The units of the spectral radiance are seen to be energy/time/area/solid angle/frequency. In MKS units this would be W·m-2·sr-1·Hz-1 (watts per square-metre-steradian-hertz).The equation of radiative transfer
The equation of radiative transfer simply says that as a beam of radiation travels, it loses energy to absorption, gains energy by emission, and redistributes energy by scattering. The differential form of the equation for radiative transfer is: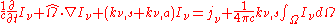
where
 is the emission coefficient,
is the emission coefficient, 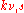 is the scattering cross section, and
is the scattering cross section, and 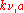 is the absorption cross section.
is the absorption cross section.Solutions to the equation of radiative transfer
Solutions to the equation of radiative transfer form an enormous body of work. The differences however, are essentially due to the various forms for the emission and absorption coefficients. If scattering is ignored, then a general solution in terms of the emission and absorption coefficients may be written:
where
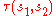 is the optical depth
is the optical depthOptical depth
Optical depth, or optical thickness, is a measure of transparency. Optical depth is defined by the negative logarithm of the fraction of radiation that is not scattered or absorbed on a path...
of the atmosphere between
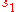 and
and 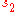 :
: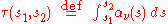
Local thermodynamic equilibrium
A particularly useful simplification of the equation of radiative transfer occurs under the conditions of local thermodynamic equilibrium (LTE). In this situation, the atmosphere consists of massive particles which are in equilibrium with each other, and therefore have a definable temperature. The radiation field is not, however in equilibrium and is being entirely driven by the presence of the massive particles. For an atmosphere in LTE, the emission coefficient and absorption coefficient are functions of temperature and density only, and are related by: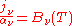
where
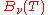 is the black body
is the black bodyBlack body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
intensity at temperature T. The solution to the equation of radiative transfer is then:
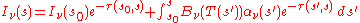
Knowing the temperature profile and the density profile of the atmospheric components will be enough to calculate a solution to the equation of radiative transfer.
The Eddington approximation
The Eddington approximation is a special case of the two stream approximationTwo stream approximation (radiative transfer)
Two-stream approximation of the radiative transfer equation is an approximation of the radiative transfer equation in which radiation is propagating in only two discrete directions....
. It can be used to obtain the spectral radiance in a plane-parallel atmosphere with isotropic frequency-independent scattering. It assumes that the intensity is a linear function of
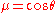 . i.e.
. i.e.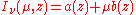
where
 is the normal direction to the slab atmosphere. Note that expressing angular integrals in terms of
is the normal direction to the slab atmosphere. Note that expressing angular integrals in terms of  simplifies things because
simplifies things because  appears in the Jacobian
appears in the JacobianJacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of integrals in spherical coordinates
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
.
Extracting the first few moments of the spectral radiance with respect to
 yields
yields

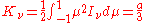
Thus the Eddington approximation is equivalent to setting
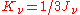 . Higher order versions of the Eddington approximation also exist, and consist of more complicated linear relations of the intensity moments. This extra equation can be used as a closure relation for the truncated system of moments.
. Higher order versions of the Eddington approximation also exist, and consist of more complicated linear relations of the intensity moments. This extra equation can be used as a closure relation for the truncated system of moments.Note that the first two moments have simple physical meanings.
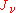 is the isotropic intensity at a point, and
is the isotropic intensity at a point, and 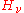 is the flux through that point in the
is the flux through that point in the  direction.
direction.The radiative transfer through an isotropically scattering atmosphere at local thermal equilibrium is given by

Integrating over all angles yields

Premultiplying by
 , and then integrating over all angles gives
, and then integrating over all angles gives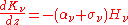
Substituting in the closure relation, and differentiating with respect to
 allows the two above equations to be combined to form the radiative diffusion equation
allows the two above equations to be combined to form the radiative diffusion equation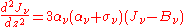
This equation shows how the effective optical depth in scattering-dominated systems may be significantly different from that given by the scattering opacity if the absorptive opacity is small.
See also
- Absorption (electromagnetic radiation)Absorption (electromagnetic radiation)In physics, absorption of electromagnetic radiation is the way by which the energy of a photon is taken up by matter, typically the electrons of an atom. Thus, the electromagnetic energy is transformed to other forms of energy for example, to heat. The absorption of light during wave propagation is...
- Atomic line spectra
- Beer-Lambert lawBeer-Lambert lawIn optics, the Beer–Lambert law, also known as Beer's law or the Lambert–Beer law or the Beer–Lambert–Bouguer law relates the absorption of light to the properties of the material through which the light is travelling.-Equations:The law states that there is a logarithmic dependence between the...
- Emission
- List of atmospheric radiative transfer codes
- ScatteringScatteringScattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
- Radiative transfer equation and diffusion theory for photon transport in biological tissueRadiative transfer equation and diffusion theory for photon transport in biological tissuePhoton transport in biological tissue can be equivalently modeled numerically with Monte Carlo simulations or analytically by the radiative transfer equation . However, the RTE is difficult to solve without introducing approximations. A common approximation summarized here is the diffusion...
- Spectral radiance
- Specific intensitySpecific radiative intensitySpecific intensity is a fundamental quantity used in theoretical physics that fully describes the field of classical electromagnetic radiation of any kind, including thermal radiation and light. It is a description based on radiometry rather than Maxwellian electromagnetic fields or photon...

