
Radiative equilibrium
Encyclopedia
Radiative equilibrium is one of the several requirements for thermodynamic equilibrium
, but it can occur in the absence of thermodynamic equilibrium. There are various types of radiative equilibrium, which is itself a kind of dynamic equilibrium
.
in 1791. Prevost considered that what is nowadays called the photon gas
or electromagnetic radiation
was a fluid that he called "free heat". Prevost's (translated) 1791 definition is as follows:
Prevost went on to comment that "The heat of several portions of space at the same temperature, and next to one another, is at the same time in the two species of equilibrium."
Prevost's contribution was often referred to as Prevost's exchange principle.
, which is a function of each geometrical point in a space region, at an instant of time. This is slightly different from Prevost’s mode of definition, which was for regions of space. It is also slightly conceptually different from Prevost’s definition: Prevost thought in terms of bound and free heat while today we think in terms of heat in kinetic and other dynamic energy of molecules, that is to say heat in matter, and the thermal photon gas
. A detailed definition is given by Goody and Yung (1989) . They think of the interconversion between thermal radiation and heat in matter. From the specific radiative intensity they derive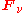 , the monochromatic vector flux density of radiation at each point in a region of space, which is equal to the time averaged monochromatic Poynting vector
, the monochromatic vector flux density of radiation at each point in a region of space, which is equal to the time averaged monochromatic Poynting vector
at that point (Mihalas 1978 on pages 9–11). They define the monochromatic volume-specific rate of gain of heat by matter from radiation as the negative of the divergence of the monochromatic flux density vector; it is a scalar function of the position of the point:
They define (pointwise) monochromatic radiative equilibrium by
They define (pointwise) radiative equilibrium by
This means that, at every point of the region of space that is in (pointwise) radiative equilibrium, the total, for all frequencies of radiation, interconversion of energy between thermal radiation and energy content in matter is nil. Pointwise radiative equilibrium is closely related to Prevost's absolute radiative equilibrium.
Mihalas and Weibel-Mihalas (1984) emphasise that this definition applies to a static medium, in which the matter is not moving. They also consider moving media.
and radiation
both operated but radiation was so much more efficient than convection that convection could be, as an approximation, neglected, and radiation could be considered predominant.
Chandrasekhar (1950, page 290) writes of a model of a stellar atmosphere
in which "there are no mechanisms, other than radiation, for transporting heat within the atmosphere ... [and] there are no sources of heat in the atmosphere." This is hardly different from Schwarzschild's 1906 approximate concept, but is more precisely stated.
(1914, page 40) refers to a condition of thermodynamic equilibrium
, in which "any two bodies or elements of bodies selected at random exchange by radiation equal amounts of heat with each other."
The term radiative exchange equilibrium can also be used to refer to two specified regions of space that exchange equal amounts of radiation by emission and absorption (even when the steady state is not one of thermodynamic equilibrium
, but is one in which some sub-processes include net transport of matter or energy including radiation). Radiative exchange equilibrium is very nearly the same as Prevost's relative radiative equilibrium.
s, there is zero net exchange between the surface and the atmosphere, while, in the window wavenumbers, there is simply direct radiation from the land-sea surface to space. A like situation occurs between adjacent layers in the turbulently mixed boundary layer
of the lower troposphere
, expressed in the so-called "cooling to space approximation", first noted by Rodgers and Walshaw (1966).
Liou (2002, page 459) and others use the term global radiative equilibrium to refer to radiative exchange equilibrium globally between the earth and extraterrestrial space; this means that, in a steady state, incoming solar radiation
absorbed by the earth and its atmosphere is equal to outgoing longwave radiation
from the earth and its atmosphere. Prevost would say then that the earth and its atmosphere regarded as a whole are in absolute radiative equilibrium. Some good texts, for example Satoh (2004), are rather cavalier here and simply refer to "radiative equilibrium", only implicitly distinguishing between pointwise and global exchange radiative equilibrium. These usages assume that the supply of energy from chemical
and nuclear reactions within the planet are negligibly small, the very opposite assumption to the one that motivates a contrary definition given hereunder.
Cox and Giuli (1968/1984) use a definition quite contrary to all the above usages. They define 'radiative equilibrium' for a star
, taken as a whole and not confining attention only to its atmosphere, when the rate of transfer as heat of energy from nuclear reactions plus viscosity
to the microscopic motions of the material particles of the star is just balanced by the transfer of energy by electromagnetic radiation from the star to space. This is a way of using the words 'radiative equilibrium' that is contrary to the above-mentioned usages. They note that a star that is radiating energy to space cannot be in a steady state of temperature distribution unless there is a supply of energy, in particular they have in mind a steady supply of energy from nuclear reactions within the star, to support the radiation to space. Likewise the condition that is used for the above definition of pointwise radiative equilibrium, namely "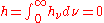 at every point of the region that is in radiative equilibrium", cannot hold throughout a star that is in a steady state of temperature distribution, without an energy supply. Their definition allows them to say at the same time that a star is in a steady state of temperature distribution and is in 'radiative equilibrium'; they are assuming that all the radiative energy to space comes from within the star, the very opposite assumption to the one made by the above-mentioned users of the concept 'global radiative equilibrium'.
at every point of the region that is in radiative equilibrium", cannot hold throughout a star that is in a steady state of temperature distribution, without an energy supply. Their definition allows them to say at the same time that a star is in a steady state of temperature distribution and is in 'radiative equilibrium'; they are assuming that all the radiative energy to space comes from within the star, the very opposite assumption to the one made by the above-mentioned users of the concept 'global radiative equilibrium'.
holds.
Two bodies in radiative exchange equilibrium, each in its own local thermodynamic equilibrium, have the same temperature and their radiative exchange complies with the Stokes-Helmholtz reciprocity principle
.
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, but it can occur in the absence of thermodynamic equilibrium. There are various types of radiative equilibrium, which is itself a kind of dynamic equilibrium
Dynamic equilibrium
A dynamic equilibrium exists once a reversible reaction ceases to change its ratio of reactants/products, but substances move between the chemicals at an equal rate, meaning there is no net change. It is a particular example of a system in a steady state...
.
Prevost's 1791 definitions
An important early contribution was made by Pierre PrevostPierre Prévost
Pierre Prévost was a Swiss philosopher and physicist. In he showed that all bodies radiate heat, no matter how hot or cold they are.-Life:...
in 1791. Prevost considered that what is nowadays called the photon gas
Photon gas
In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon - including pressure, temperature, and entropy...
or electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
was a fluid that he called "free heat". Prevost's (translated) 1791 definition is as follows:
Absolute equilibrium of free heat is the state of this fluid in a portion of space which receives as much of it as it lets escape.
Relative equilibrium of free heat is the state of this fluid in two portions of space which receive from each other equal quantities of heat, and which moreover are in absolute equilibrium, or experience precisely equal changes.
Prevost went on to comment that "The heat of several portions of space at the same temperature, and next to one another, is at the same time in the two species of equilibrium."
Prevost's contribution was often referred to as Prevost's exchange principle.
Pointwise radiative equilibrium
Following Planck (1914), a radiative field is often described in terms of specific radiative intensitySpecific radiative intensity
Specific intensity is a fundamental quantity used in theoretical physics that fully describes the field of classical electromagnetic radiation of any kind, including thermal radiation and light. It is a description based on radiometry rather than Maxwellian electromagnetic fields or photon...
, which is a function of each geometrical point in a space region, at an instant of time. This is slightly different from Prevost’s mode of definition, which was for regions of space. It is also slightly conceptually different from Prevost’s definition: Prevost thought in terms of bound and free heat while today we think in terms of heat in kinetic and other dynamic energy of molecules, that is to say heat in matter, and the thermal photon gas
Photon gas
In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon - including pressure, temperature, and entropy...
. A detailed definition is given by Goody and Yung (1989) . They think of the interconversion between thermal radiation and heat in matter. From the specific radiative intensity they derive
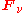 , the monochromatic vector flux density of radiation at each point in a region of space, which is equal to the time averaged monochromatic Poynting vector
, the monochromatic vector flux density of radiation at each point in a region of space, which is equal to the time averaged monochromatic Poynting vectorPoynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
at that point (Mihalas 1978 on pages 9–11). They define the monochromatic volume-specific rate of gain of heat by matter from radiation as the negative of the divergence of the monochromatic flux density vector; it is a scalar function of the position of the point:
-
-
-
 .
.
-
-
They define (pointwise) monochromatic radiative equilibrium by
-
-
-
 at every point of the region that is in radiative equilibrium.
at every point of the region that is in radiative equilibrium.
-
-
They define (pointwise) radiative equilibrium by
-
-
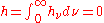 at every point of the region that is in radiative equilibrium.
at every point of the region that is in radiative equilibrium.
-
This means that, at every point of the region of space that is in (pointwise) radiative equilibrium, the total, for all frequencies of radiation, interconversion of energy between thermal radiation and energy content in matter is nil. Pointwise radiative equilibrium is closely related to Prevost's absolute radiative equilibrium.
Mihalas and Weibel-Mihalas (1984) emphasise that this definition applies to a static medium, in which the matter is not moving. They also consider moving media.
Approximate pointwise radiative equilibrium
K. Schwarzschild in 1906 considered a system in which convectionConvection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
and radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
both operated but radiation was so much more efficient than convection that convection could be, as an approximation, neglected, and radiation could be considered predominant.
Chandrasekhar (1950, page 290) writes of a model of a stellar atmosphere
Stellar atmosphere
The stellar atmosphere is the outer region of the volume of a star, lying above the stellar core, radiation zone and convection zone. It is divided into several regions of distinct character:...
in which "there are no mechanisms, other than radiation, for transporting heat within the atmosphere ... [and] there are no sources of heat in the atmosphere." This is hardly different from Schwarzschild's 1906 approximate concept, but is more precisely stated.
Radiative exchange equilibrium
PlanckMax Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
(1914, page 40) refers to a condition of thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, in which "any two bodies or elements of bodies selected at random exchange by radiation equal amounts of heat with each other."
The term radiative exchange equilibrium can also be used to refer to two specified regions of space that exchange equal amounts of radiation by emission and absorption (even when the steady state is not one of thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, but is one in which some sub-processes include net transport of matter or energy including radiation). Radiative exchange equilibrium is very nearly the same as Prevost's relative radiative equilibrium.
Approximate radiative exchange equilibrium
To a first approximation, an example of radiative exchange equilibrium is in the exchange of non-window wavelength thermal radiation between the land-and-sea surface and the lowest atmosphere, when there is a clear sky. As a first approximation (Swinbank 1963, Paltridge and Platt 1976, pages 139-140), in the non-window wavenumberWavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
s, there is zero net exchange between the surface and the atmosphere, while, in the window wavenumbers, there is simply direct radiation from the land-sea surface to space. A like situation occurs between adjacent layers in the turbulently mixed boundary layer
Planetary boundary layer
The planetary boundary layer , also known as the atmospheric boundary layer , is the lowest part of the atmosphere and its behavior is directly influenced by its contact with a planetary surface. On Earth it usually responds to changes in surface forcing in an hour or less...
of the lower troposphere
Troposphere
The troposphere is the lowest portion of Earth's atmosphere. It contains approximately 80% of the atmosphere's mass and 99% of its water vapor and aerosols....
, expressed in the so-called "cooling to space approximation", first noted by Rodgers and Walshaw (1966).
Definition for an entire passive celestial system such as a planet that does not supply its own energy
Global radiative equilibrium
Liou (2002, page 459) and others use the term global radiative equilibrium to refer to radiative exchange equilibrium globally between the earth and extraterrestrial space; this means that, in a steady state, incoming solar radiation
Sunlight
Sunlight, in the broad sense, is the total frequency spectrum of electromagnetic radiation given off by the Sun. On Earth, sunlight is filtered through the Earth's atmosphere, and solar radiation is obvious as daylight when the Sun is above the horizon.When the direct solar radiation is not blocked...
absorbed by the earth and its atmosphere is equal to outgoing longwave radiation
Outgoing longwave radiation
Outgoing Longwave Radiation is the energy leaving the earth as infrared radiation at low energy. OLR is a critical component of the Earth’s radiation budget and represents the total radiation going to space emitted by the atmosphere...
from the earth and its atmosphere. Prevost would say then that the earth and its atmosphere regarded as a whole are in absolute radiative equilibrium. Some good texts, for example Satoh (2004), are rather cavalier here and simply refer to "radiative equilibrium", only implicitly distinguishing between pointwise and global exchange radiative equilibrium. These usages assume that the supply of energy from chemical
Chemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
and nuclear reactions within the planet are negligibly small, the very opposite assumption to the one that motivates a contrary definition given hereunder.
A contrary definition
Cox and Giuli (1968/1984) use a definition quite contrary to all the above usages. They define 'radiative equilibrium' for a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
, taken as a whole and not confining attention only to its atmosphere, when the rate of transfer as heat of energy from nuclear reactions plus viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
to the microscopic motions of the material particles of the star is just balanced by the transfer of energy by electromagnetic radiation from the star to space. This is a way of using the words 'radiative equilibrium' that is contrary to the above-mentioned usages. They note that a star that is radiating energy to space cannot be in a steady state of temperature distribution unless there is a supply of energy, in particular they have in mind a steady supply of energy from nuclear reactions within the star, to support the radiation to space. Likewise the condition that is used for the above definition of pointwise radiative equilibrium, namely "
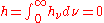 at every point of the region that is in radiative equilibrium", cannot hold throughout a star that is in a steady state of temperature distribution, without an energy supply. Their definition allows them to say at the same time that a star is in a steady state of temperature distribution and is in 'radiative equilibrium'; they are assuming that all the radiative energy to space comes from within the star, the very opposite assumption to the one made by the above-mentioned users of the concept 'global radiative equilibrium'.
at every point of the region that is in radiative equilibrium", cannot hold throughout a star that is in a steady state of temperature distribution, without an energy supply. Their definition allows them to say at the same time that a star is in a steady state of temperature distribution and is in 'radiative equilibrium'; they are assuming that all the radiative energy to space comes from within the star, the very opposite assumption to the one made by the above-mentioned users of the concept 'global radiative equilibrium'.Mechanisms of radiative equilibrium
When there is enough matter in a region to allow molecular collisions to occur very much more often than creation or annihilation of photons, for radiation one speaks of local thermodynamic equilibrium. In this case, Kirchhoff's law of equality of radiative absorptivity and emissivityKirchhoff's law of thermal radiation
In thermodynamics, Kirchhoff's law of thermal radiation, or Kirchhoff's law for short, is a general statement equating emission and absorption in heated objects, proposed by Gustav Kirchhoff in 1859, following from general considerations of thermodynamic equilibrium and detailed balance.An object...
holds.
Two bodies in radiative exchange equilibrium, each in its own local thermodynamic equilibrium, have the same temperature and their radiative exchange complies with the Stokes-Helmholtz reciprocity principle
Helmholtz reciprocity
The Helmholtz reciprocity principle describes how a ray of light and its reverse ray encounter matched optical adventures, such as reflections, refractions, and absorptions in a passive medium, or at an interface....
.

