Quaternionic projective space
Encyclopedia
In mathematics
, quaternionic projective space is an extension of the ideas of real projective space
and complex projective space
, to the case where coordinates lie in the ring of quaternion
s H. Quaternionic projective space of dimension n is usually denoted by
and is a closed manifold
of (real) dimension 4n. It is a homogeneous space
for a Lie group
action, in more than one way.
of a point can be written
where the qi are quaternions, not all zero. Two sets of coordinates represent the same point if they are 'proportional' by a left multiplication by a non-zero quaternion c; that is, we identify all the
In the language of group action
s, HPn is the orbit space of Hn+1-(0, ..., 0) by the action of H*, the multiplicative group of non-zero quaternions. By first projecting onto the unit sphere inside Hn+1 one may also regard HPn as the orbit space of S4n+3 by the action of Sp(1), the group of unit quaternions. The sphere S4n+3 then becomes a principal Sp(1)-bundle
over HPn: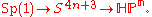
There is also a construction of HPn by means of two-dimensional complex subspaces of C2n, meaning that HPn lies inside a complex Grassmannian
.
for the uses of the projective line of the arbitrary ring
.
From the topological point of view the quaternionic projective line is the 4-sphere, and in fact these are diffeomorphic manifolds. The fibration mentioned previously is from the 7-sphere, and is an example of a Hopf fibration.
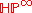is the classifying space
BS3; and, rationally (i.e. after localisation of a space it is an Eilenberg–Maclane space K(Z,4) (cf. the example K(Z,2)). See rational homotopy theory
.
may be taken, writing U(1) for the circle group. It has been shown that this quotient is the 7-sphere
, a result of Vladimir Arnold
from 1996, later rediscovered by Edward Witten
and Michael Atiyah
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, quaternionic projective space is an extension of the ideas of real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
and complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, to the case where coordinates lie in the ring of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s H. Quaternionic projective space of dimension n is usually denoted by
- HPn
and is a closed manifold
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
of (real) dimension 4n. It is a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
for a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
action, in more than one way.
In coordinates
Its direct construction is as a special case of the projective space over a division algebra. The homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
of a point can be written
- [
where the qi are quaternions, not all zero. Two sets of coordinates represent the same point if they are 'proportional' by a left multiplication by a non-zero quaternion c; that is, we identify all the
- [
In the language of group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s, HPn is the orbit space of Hn+1-(0, ..., 0) by the action of H*, the multiplicative group of non-zero quaternions. By first projecting onto the unit sphere inside Hn+1 one may also regard HPn as the orbit space of S4n+3 by the action of Sp(1), the group of unit quaternions. The sphere S4n+3 then becomes a principal Sp(1)-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over HPn:
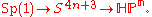
There is also a construction of HPn by means of two-dimensional complex subspaces of C2n, meaning that HPn lies inside a complex Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
.
Projective line
The one-dimensional projective space over H is called the "projective line" in generalization of the complex projective line. For example, it was used (implicitly) in 1947 by P. G. Gormley to extend the Möbius group to the quaternion context with "linear fractional transformations". See inversive ring geometryInversive ring geometry
In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....
for the uses of the projective line of the arbitrary ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
From the topological point of view the quaternionic projective line is the 4-sphere, and in fact these are diffeomorphic manifolds. The fibration mentioned previously is from the 7-sphere, and is an example of a Hopf fibration.
Infinite-dimensional quaternionic projective space
The space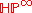 is the classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BS3; and, rationally (i.e. after localisation of a space it is an Eilenberg–Maclane space K(Z,4) (cf. the example K(Z,2)). See rational homotopy theory
Rational homotopy theory
In mathematics, rational homotopy theory is the study of the rational homotopy type of a space, which means roughly that one ignores all torsion in the homotopy groups...
.
Quaternionic projective plane
The 8-dimensional HP2 has a circle action, by the group of complex scalars of absolute value 1 acting on the other side (so on the right, as the convention for the action of c above is on the left). Therefore the quotient manifoldmay be taken, writing U(1) for the circle group. It has been shown that this quotient is the 7-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, a result of Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
from 1996, later rediscovered by Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
and Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
.
Further reading
- V. I. Arnol'd, Relatives of the Quotient of the Complex Projective Plane by the Complex Conjugation, Tr. Mat. Inst. Steklova, 1999, Volume 224, Pages 56–67. Treats the analogue of the result mentioned for quaternionic projective space and the 13-sphere.