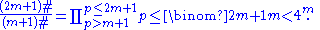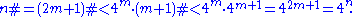Proof of Bertrand's postulate
Encyclopedia
In mathematics
, Bertrand's postulate (actually a theorem
) states that for each n ≥ 2 there is a prime
p such that n < p < 2n. It was first proven by Pafnuty Chebyshev
, and a short but advanced proof was given by Srinivasa Ramanujan
. The gist of the following elementary but involved proof by contradiction is due to Paul Erdős; the basic idea of the proof is to show that a certain binomial coefficient
needs to have a prime factor
within the desired interval in order to be large enough.
The argument in the proof establishes a contradiction by comparing two facts:
It is then shown by some extended computation (relying mostly on Lemma 2 and Lemma 4) that the second fact is inconsistent with the first one. Therefore Bertrand's postulate must hold. In order to present the main argument of the proof intelligibly, these lemmas and a few auxiliary claims are proved separately first.
Proof: Applying the binomial theorem
,
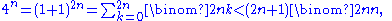
since
is the largest term in the sum, and the sum has 2n+1 terms.
Lemma: For any p, we have pR(p,n) ≤ 2n.
Proof: The exponent of p in n! is (see Factorial#Number theory):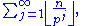
so we get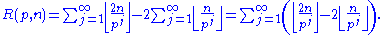
But each term of the last summation can either be 0 (if n / pj mod 1 < 1/2) or 1 (if n / pj mod 1 ≥ 1/2) and all terms with j > logp(2n) are 0. Therefore
and we get: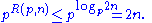
This completes the proof of the lemma.
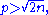we have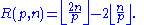
Proof: Using the same sum for R(p,n) as in Lemma 2, we see that since p2 > 2n, in fact only the first term is nonzero; this term is exactly the right-hand side of the above equation.
function,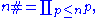
where the product is taken over all prime numbers p less than or equal to n.
Lemma: For all n ≥ 1, we have n# < 4n.
Proof: The proof is by mathematical induction
. First the base cases:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Bertrand's postulate (actually a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
) states that for each n ≥ 2 there is a prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p such that n < p < 2n. It was first proven by Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
, and a short but advanced proof was given by Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
. The gist of the following elementary but involved proof by contradiction is due to Paul Erdős; the basic idea of the proof is to show that a certain binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
needs to have a prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
within the desired interval in order to be large enough.
The argument in the proof establishes a contradiction by comparing two facts:
- The binomial coefficient
is "large" in a precise sense (Lemma 1), and - If Bertrand's postulate fails for n, then all of the prime factors of this binomial coefficient are "small" (a combination of Lemma 3 and the negation of Bertrand's postulate).
It is then shown by some extended computation (relying mostly on Lemma 2 and Lemma 4) that the second fact is inconsistent with the first one. Therefore Bertrand's postulate must hold. In order to present the main argument of the proof intelligibly, these lemmas and a few auxiliary claims are proved separately first.
Lemma 1: A lower bound on the central binomial coefficients
Lemma: For any integer n > 0, we haveProof: Applying the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
,
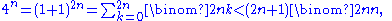
since
is the largest term in the sum, and the sum has 2n+1 terms.Lemma 2: An upper bound on prime powers dividing central binomial coefficients
For a fixed prime p, define R(p,n) to be the highest natural number x, such that px dividesLemma: For any p, we have pR(p,n) ≤ 2n.
Proof: The exponent of p in n! is (see Factorial#Number theory):
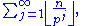
so we get
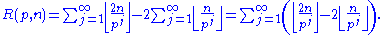
But each term of the last summation can either be 0 (if n / pj mod 1 < 1/2) or 1 (if n / pj mod 1 ≥ 1/2) and all terms with j > logp(2n) are 0. Therefore
and we get:
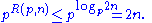
This completes the proof of the lemma.
Lemma 3: The exact power of a large prime in a central binomial coefficient
Lemma: For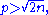 we have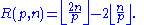Proof: Using the same sum for R(p,n) as in Lemma 2, we see that since p2 > 2n, in fact only the first term is nonzero; this term is exactly the right-hand side of the above equation.
Lemma 4: An upper bound on the primorial
We estimate the primorialPrimorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
function,
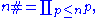
where the product is taken over all prime numbers p less than or equal to n.
Lemma: For all n ≥ 1, we have n# < 4n.
Proof: The proof is by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. First the base cases:
- n = 1: n# is the empty productEmpty productIn mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
:
-
- n = 2: 2 is prime:
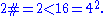
- n > 2 and n is even: Since every even number greater than 2 is composite, we have by the induction hypothesis:
- n > 2 is odd. Let n = 2m + 1 with m > 0; then since all the terms in the following binomial expansion are positive we have:
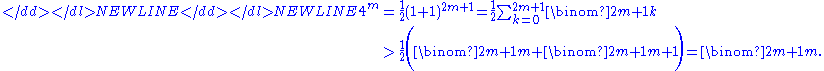
- Each prime p with m + 1 < p ≤ 2m + 1 divides
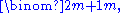giving us:
- By induction, (m + 1)# < 4m + 1, so:
Thus the lemma is proven.
Computation
We collect here a numerical claim which comes up in the proof.- If
, then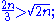 
To prove 1, observe that
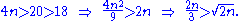
Proof of Bertrand's Postulate
Assume there is a counterexampleCounterexampleIn logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
: an integer n ≥ 2 such that there is no prime p with n < p < 2n.
If 2 ≤ n < 468, then p can be chosen from among the prime numbers 3, 5, 7, 13, 23, 43, 83, 163, 317, 631 (each being less than twice its predecessor) such that n < p < 2n. Therefore n ≥ 468.
There are no prime factors p of
such that:
- 2n < p, because every factor must divide (2n)!;
- p = 2n, because 2n is not prime;
- n < p < 2n, because we assumed there is no such prime number;
- 2n / 3 < p ≤ n: by computation 1 we have
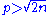, so Lemma 3 applies, and by rearranging the inequalities 2n/3 < p and n ≥ p we deduce that n/p ≥ 1 and 2n/p < 3. Combining these results, we get
Therefore, every prime factor p satisfies p ≤ 2n/3.
When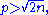
the number 
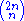has at most one factor of p. By Lemma 2, for any prime p we have pR(p,n) ≤ 2n, so the product of the pR(p,n) over the primes less than or equal to 
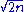is at most 
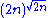. Then, starting with Lemma 1 and decomposing the right-hand side into its prime factorization, these bounds give: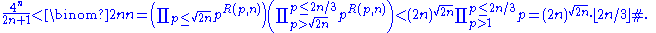
Using Lemma 4, this simplifies: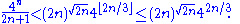
This gives us the contradiction: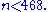
Thus no counterexample to the postulate is possible.- Each prime p with m + 1 < p ≤ 2m + 1 divides
