
Principal quantum number
Encyclopedia
In atomic physics
, the principal quantum symbolized as n is the first
of a set of quantum number
s (which includes: the principal quantum number, the azimuthal quantum number
, the magnetic quantum number
, and the spin quantum number
) of an atomic orbital
. The principal quantum number can only have positive integer
values. As n increases, the orbital becomes larger and the electron spends more time farther from the nucleus. As n increases, the electron is also at a higher potential energy and is therefore less tightly bound to the nucleus. This is the only quantum number introduced by the Bohr model.
For an analogy, one could imagine a multistoried building with an elevator structure. The building has an integral number of floors, and a (well-functioning) elevator can only stop at a particular floor. Furthermore the elevator can only travel an integer number of levels. As with the principal quantum number, higher numbers are associated with higher potential energy.
Of course beyond this point the analogy breaks down. In the case of elevators the potential energy is gravitational but with the quantum number it is electromagnetic. The gains and losses in energy are approximate with the elevator, but precise with quantum state. The elevator ride from floor to floor is continuous whereas quantum transitions are discontinuous. Finally the constraints of elevator design are imposed by the requirements of architecture, but quantum behavior reflects fundamental laws of physics.
or orbital
. Two electrons belonging to the same atom can not have the same four quantum numbers, due to the Pauli exclusion principle
. The wavefunction of the Schrödinger wave equation
reduces to the three equations that when solved lead to the first three quantum numbers. Therefore, the equations for the first three quantum numbers are all interrelated. The principal quantum number arose in the solution of the radial part of the wave equation as shown below.
The Schrödinger wave equation describes energy eigenstates having corresponding real numbers En with a definite total energy which the value of En defines. The bound state energies of the electron in the hydrogen atom are given by:
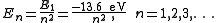
The parameter n can take only positive integer values. The concept of energy levels and notation was utilized from the earlier Bohr model of the atom. Schrödinger's equation developed the idea from a flat two-dimensional Bohr atom to the three-dimensional wave function model.
In the Bohr model, the allowed orbits were derived from quantized (discrete) values of orbital angular momentum
, L according to the equation
where n = 1, 2, 3, … and is called the principal quantum number, and h is Planck's constant. This formula is not correct in quantum mechanics as the angular momentum magnitude is described by the azimuthal quantum number
, but the energy levels are accurate and classically they correspond to the sum of potential and kinetic energy of the electron.
The principal quantum number n represents the relative overall energy of each orbital, and the energy of each orbital increases as the distance from the nucleus increases. The sets of orbitals with the same n value are often referred to as electron shells or energy level
s.
The minimum energy exchanged during any wave-matter interaction is the wave frequency multiplied by Planck's constant. This causes the wave to display particle-like packets of energy called quanta
. The difference between energy levels that have different n determine the Emission spectrum
of the element.
In the notation of the periodic table, the main shells of electrons are labeled:
based on the principal quantum number.
The principal quantum number is related to the radial quantum number, nr, by:
where ℓ is the azimuthal quantum number
and nr is equal to the number of nodes
in the radial wavefunction.
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
, the principal quantum symbolized as n is the first
of a set of quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s (which includes: the principal quantum number, the azimuthal quantum number
Azimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
, the magnetic quantum number
Magnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
, and the spin quantum number
Spin quantum number
In atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum of a given particle...
) of an atomic orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
. The principal quantum number can only have positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
values. As n increases, the orbital becomes larger and the electron spends more time farther from the nucleus. As n increases, the electron is also at a higher potential energy and is therefore less tightly bound to the nucleus. This is the only quantum number introduced by the Bohr model.
For an analogy, one could imagine a multistoried building with an elevator structure. The building has an integral number of floors, and a (well-functioning) elevator can only stop at a particular floor. Furthermore the elevator can only travel an integer number of levels. As with the principal quantum number, higher numbers are associated with higher potential energy.
Of course beyond this point the analogy breaks down. In the case of elevators the potential energy is gravitational but with the quantum number it is electromagnetic. The gains and losses in energy are approximate with the elevator, but precise with quantum state. The elevator ride from floor to floor is continuous whereas quantum transitions are discontinuous. Finally the constraints of elevator design are imposed by the requirements of architecture, but quantum behavior reflects fundamental laws of physics.
Derivation
There are a set of quantum numbers associated with the energy states of the atom. The four quantum numbers n, ℓ, m, and s specify the complete and unique quantum state of a single electron in an atom called its wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
or orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
. Two electrons belonging to the same atom can not have the same four quantum numbers, due to the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
. The wavefunction of the Schrödinger wave equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
reduces to the three equations that when solved lead to the first three quantum numbers. Therefore, the equations for the first three quantum numbers are all interrelated. The principal quantum number arose in the solution of the radial part of the wave equation as shown below.
The Schrödinger wave equation describes energy eigenstates having corresponding real numbers En with a definite total energy which the value of En defines. The bound state energies of the electron in the hydrogen atom are given by:
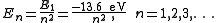
The parameter n can take only positive integer values. The concept of energy levels and notation was utilized from the earlier Bohr model of the atom. Schrödinger's equation developed the idea from a flat two-dimensional Bohr atom to the three-dimensional wave function model.
In the Bohr model, the allowed orbits were derived from quantized (discrete) values of orbital angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, L according to the equation
where n = 1, 2, 3, … and is called the principal quantum number, and h is Planck's constant. This formula is not correct in quantum mechanics as the angular momentum magnitude is described by the azimuthal quantum number
Azimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
, but the energy levels are accurate and classically they correspond to the sum of potential and kinetic energy of the electron.
The principal quantum number n represents the relative overall energy of each orbital, and the energy of each orbital increases as the distance from the nucleus increases. The sets of orbitals with the same n value are often referred to as electron shells or energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
s.
The minimum energy exchanged during any wave-matter interaction is the wave frequency multiplied by Planck's constant. This causes the wave to display particle-like packets of energy called quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
. The difference between energy levels that have different n determine the Emission spectrum
Emission spectrum
The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted by the element's atoms or the compound's molecules when they are returned to a lower energy state....
of the element.
In the notation of the periodic table, the main shells of electrons are labeled:
- K (n = 1), L (n = 2), M (n = 3), etc.
based on the principal quantum number.
The principal quantum number is related to the radial quantum number, nr, by:
where ℓ is the azimuthal quantum number
Azimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
and nr is equal to the number of nodes
Node (physics)
A node is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the...
in the radial wavefunction.
See also
- Total angular momentum quantum number
- Basic quantum mechanics
- Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....



