
Primon gas
Encyclopedia
In mathematical physics
, the primon gas or free Riemann gas is a toy model
illustrating in a simple way some correspondences between number theory
and ideas in quantum field theory
and dynamical systems. It is a quantum field theory of a set of non-interacting particles, the primons; it is called a gas
or a free model because the particles are non-interacting. The idea of the primon gas was independently discovered by
Donald Spectorand Bernard Julia
. Later works by Bakas and
Bowick
and Spector explored the connection of such systems to
string theory.
 labelled by the prime number
labelled by the prime number
s p, and having energies proportional to log p. That is,
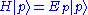
with
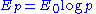
The second-quantized version of this Hamiltonian converts states into particles, the primons. A multi-particle state is given by the numbers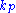 of primons in the single-particle states
of primons in the single-particle states 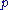 :
:
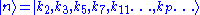
This corresponds to the factorization of into primes:
into primes:
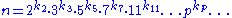
The labelling by the integer n is unique, since every number has a unique factorization into primes.
The energy of such a multi-particle state is clearly
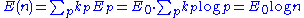
The statistical mechanics partition function
Z is given by the Riemann zeta function:
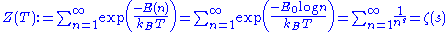
with s = E0/kBT where kB is Boltzmann's constant and T is the absolute temperature
. The divergence of the zeta function at s = 1 corresponds to the divergence of the partition function at a Hagedorn temperature
of TH = E0/kB.
s. If the particles are taken to be fermion
s, then the Pauli exclusion principle
prohibits multi-particle states which include squares of primes. By the spin-statistics theorem
, field states with an even number of particles are bosons, while those with an odd number of particles are fermions. The fermion operator (−1)F
has a very concrete realization in this model as the Möbius function
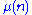 , in that the Mobius function is positive for bosons, negative for fermions, and zero on exclusion-principle-prohibited states.
, in that the Mobius function is positive for bosons, negative for fermions, and zero on exclusion-principle-prohibited states.
, where, corresponding to the example above, the spectrum of a ring
takes the role of the spectrum of energy eigenvalues, the prime ideal
s take the role of the prime numbers, the group representation
s take the role of integers, group characters taking the place the Dirichlet character
s, and so on.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the primon gas or free Riemann gas is a toy model
Toy model
In physics, a toy model is a simplified set of objects and equations relating them that can nevertheless be used to understand a mechanism that is also useful in the full, non-simplified theory....
illustrating in a simple way some correspondences between number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and ideas in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and dynamical systems. It is a quantum field theory of a set of non-interacting particles, the primons; it is called a gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
or a free model because the particles are non-interacting. The idea of the primon gas was independently discovered by
Donald Spectorand Bernard Julia
Bernard Julia
Bernard Julia is a French theoretical physicist who has made contributions to the theory of supergravity. He graduated from Université Paris-Sud in 1978,and is directeur de recherche at the Ecole Normale Supérieure...
. Later works by Bakas and
Bowick
and Spector explored the connection of such systems to
string theory.
The model
Consider a simple quantum Hamiltonian H having eigenstates labelled by the prime number
labelled by the prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s p, and having energies proportional to log p. That is,
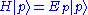
with
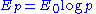
The second-quantized version of this Hamiltonian converts states into particles, the primons. A multi-particle state is given by the numbers
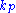 of primons in the single-particle states
of primons in the single-particle states 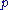 :
: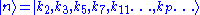
This corresponds to the factorization of
 into primes:
into primes: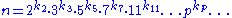
The labelling by the integer n is unique, since every number has a unique factorization into primes.
The energy of such a multi-particle state is clearly
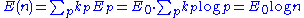
The statistical mechanics partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
Z is given by the Riemann zeta function:
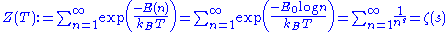
with s = E0/kBT where kB is Boltzmann's constant and T is the absolute temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. The divergence of the zeta function at s = 1 corresponds to the divergence of the partition function at a Hagedorn temperature
Hagedorn temperature
The Hagedorn temperature in theoretical physics is the temperature above which the partition sum diverges in a system with exponential growth in the density of states. It is named after German physicist Rolf Hagedorn.Phase transitions The Hagedorn temperature in theoretical physics is the...
of TH = E0/kB.
The supersymmetric model
The above second-quantized model takes the particles to be bosonBoson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s. If the particles are taken to be fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s, then the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
prohibits multi-particle states which include squares of primes. By the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
, field states with an even number of particles are bosons, while those with an odd number of particles are fermions. The fermion operator (−1)F
(-1)^F
In a quantum field theory with fermions, F is a unitary, Hermitian, involutive operator which multiplies bosonic states by 1 and fermionic states by −1. This is always a global internal symmetry of any quantum field theory with fermions and corresponds to a rotation by 2π. This splits the Hilbert...
has a very concrete realization in this model as the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
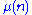 , in that the Mobius function is positive for bosons, negative for fermions, and zero on exclusion-principle-prohibited states.
, in that the Mobius function is positive for bosons, negative for fermions, and zero on exclusion-principle-prohibited states.More complex models
The connections between number theory and quantum field theory can be somewhat further extended into connections between topological field theory and K-theoryK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, where, corresponding to the example above, the spectrum of a ring
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
takes the role of the spectrum of energy eigenvalues, the prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s take the role of the prime numbers, the group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s take the role of integers, group characters taking the place the Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
s, and so on.

